To the Wire

Problem One

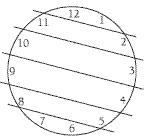
The solutions for a and b below show that there is only one way to break the clock into either six or three regions so that the sums of the numbers in each region are the same.
a. The sum of all the numbers from 1 to 12 is 78. So the sum in each of the six regions has to be 78 ÷ 6 = 13.
What goes with 12 to get 13? Clearly, it has to go with the 1. In the same way, 11 goes with 2, 10 with 3, 9 with 4, 8 with 5, and 7 with 6. These are the six regions.

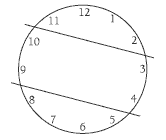
b. With three regions, the sum of each region has to be 78 ÷ 3 = 26. What does 12 go with?
It can’t go with 10 and 11 because 10 + 11 + 12 = 33, which is too big. It can’t go without the 11 because 12 + 1 + 2 + 3 + 4 = 22 (not enough) and 12 + 1 + 2 + 3 + 4 + 5 = 27 (too big). But 11 + 12 = 23, and you can get the extra 3 you need by adding in 1 + 2. So the region containing 12 also contains 11, 1, and 2.
What numbers are in the region with 10? This region can’t contain 8 because
10 + 9 + 8 = 27, and that’s too big. On the other hand, 9 must be in with 10 because
10 + 3 + 4 + 5 = 22 (not enough) and 10 + 3 + 4 + 5 + 6 = 28 (too big). So you have to have 10 + 9 + 3 + 4. That leaves 5 + 6 + 7 + 8 = 26.

There is a method for adding consecutive numbers together. For example, to add the numbers 1 to 12 together:
sum = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12
= (1 + 12) + (2 + 11) + (3 + 10) + (4 + 9) + (5 + 8) + (6 + 7)
= 6 x 13
= 78.
The sum of the first and last numbers is the same as the sum of the second and second to last numbers, which is the same as the third and third to last numbers, and so on. There are six sums that add up to 13, so the sum is 78.
The sum of consecutive numbers is always the sum of the first and the last terms multiplied by half the number of terms (even if the number of terms is odd). For example, 12 + 1 = 13, 13 x 6 = 78.
You could show the students this method as a way of making them more aware of the power of maths.
Extension
a. “Are there other regions (for example, two or four) that you can break the clock up into, with the numbers in each region adding to the same total? If you can, can this be done in only one way?”
b. You might like to ask the students to explore other possible “clocks”. “What happens if you have a 10 hour clock or a 24 hour clock? In how many ways can the numbers be divided into regions then?”

Problem Two

Melody did two deals and made $15 on the first one and $20 on the second. Altogether she made a profit of $35. (The fact that she paid $75 to start with is only relevant when calculating her profit on the first guitar.)
Students can easily make up their own problems like this. You can also rearrange the problem to make it more difficult. For example, suppose Melody bought her first guitar for $55. She bought her second guitar for $70 and sold it for $90. If she made a total profit of $60, how much did she sell her first guitar for?
There are essentially five numbers involved in this problem: the cost of each of the two guitars, the sale price of each of the two guitars, and Melody’s profit. The problem can be arranged so that any of these is the unknown.
Extension
“In the initial problem, how do you know that Melody must have had at least $85 before she started?”

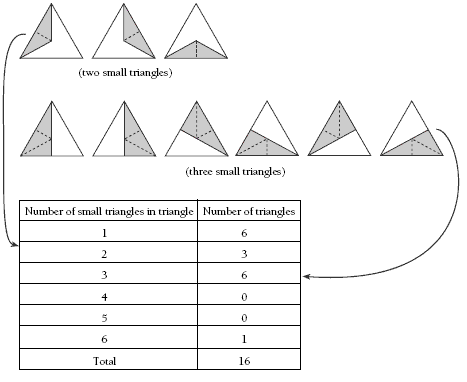
Problem Three

Students need to work systematically to count the number of triangles. First, they could count the number of triangles made up of one small triangle. Then they could count the number of triangles made up of two small triangles, and so on up to the number of triangles made up of six small triangles. They could record their results on a table.

Problem Four

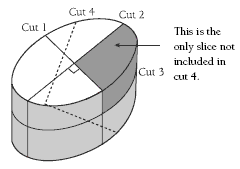
Provide the students with Plasticine or play dough and a plastic knife so that they can experiment with different cuts. Some students will find this easier than drawing the cuts on paper.
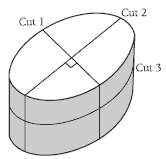
a. It is possible to cut the cheese so that each cut slices every existing piece in half. You then get 2 x 2 x 2 = 8 pieces.
To get the eight pieces, first cut vertically through the centre of the cheese (thus cutting through the diameter). Then cut vertically again, but this time make the cut at 90° to the first cut. Then make a horizontal cut. (See the diagram in the Answers.)
b. You can get 15 pieces by making a diagonal cut through seven of the eight pieces from a. There seems to be no way that a single slice can go through all of the eight pieces from a. You may need to model this with your class because it is not easy to draw in a diagram. The diagram in the Answers may help.
Extension
“How many pieces can you make with the next (fifth) cut? And the next?”
This problem is similar to the pizza problem in Problem Three, page 22.

Hints for Students

1. Start by finding the sum of the numbers from 1 to 12. Then work out the total that the numbers in each region should add up to. What goes with 12?
2. How much profit did Melody make on each of her deals?
3. You need to work systematically here.
First count the number of triangles made up of one triangle, then two, then three, and so on.
4. What might you hope to do every time you cut this cheese? (Think of fractions.)
Can you always do it?

Answers to Problems

1. a. The clock can be divided into six regions with numbers that add up to 13:

b. Yes. Each of the three regions adds up to 26.

2. $35. (The original $75 was not part of the money that she “made”.)
3. 16
4. a. 8 (two vertical cuts and one horizontal cut)

b. 15. The fourth cut is an angled (slanted) cut that goes through seven of the eight
pieces in a.