The purpose of this activity is to engage students in evaluating another’s judgement about the fairness of a game of chance and investigating the fairness of their own game.
This activity assumes the students have experience in the following areas:
- Trialling simple experiments with coins and dice.
- Finding all the possible outcomes for simple chance situations.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
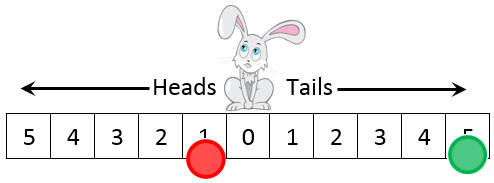
Henry’s counter is red and Wiremu’s is green.
Henry says that the game isn’t fair.
- Do you agree with Henry? Explain why.
- Change one rule in the game, play it with a friend and decide if your game is fair.
Bunny Hop
- Each player needs a counter and a coin.
- Place the counters on zero.
- Take turns tossing a coin.
If it shows tails, move one space to the right.
If it shows heads, move one space to the left. - The winner is the player who is on the highest number after 10 tosses each.
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- Do I understand how the game is played? (Students will benefit from playing the game themselves a few times.)
- What does fair mean when you are talking about a game? (Fair means that both players have an equal chance of winning.)
- What are the rules of the game that might be changed?
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- How can you find out if a game is fair, or not?
- How many games do you need to play to find out if it is fair?
- Are there ways to find all the things that might happen in a game?
- Will finding all the possible outcomes be sensible with this game? Why?
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Am I recording the results of the trials in an organised way?
- Have I played enough games, or do I need to play more? Why?
- Do the results of the game match my thinking? Why do the results vary from my predictions?
- How can I record what happened using numbers, especially fractions or percentages.
- What variation to the game have I made up?
- How do I find out if that game is fair?
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- What is my answer? Does my answer show that the game is fair, or not?
- How would I convince someone else that the game is fair, or not?
- Did I try and game? Did I find all the possible outcomes?
- Do the trail results and possible outcome match? Why might that happen?
- What could I find out next?
Examples of work
Work sample 1
The student alters the rules of a game to make it fair. They realise that they need to play many games to find out if their revised game is fair to both players.
Click on the image to enlarge it. Click again to close.
Work sample 2
The student conjectures that the original ganme is fair because the conditions for both players are the same. They adapt one rule in the game and explain why the variation is still fair.