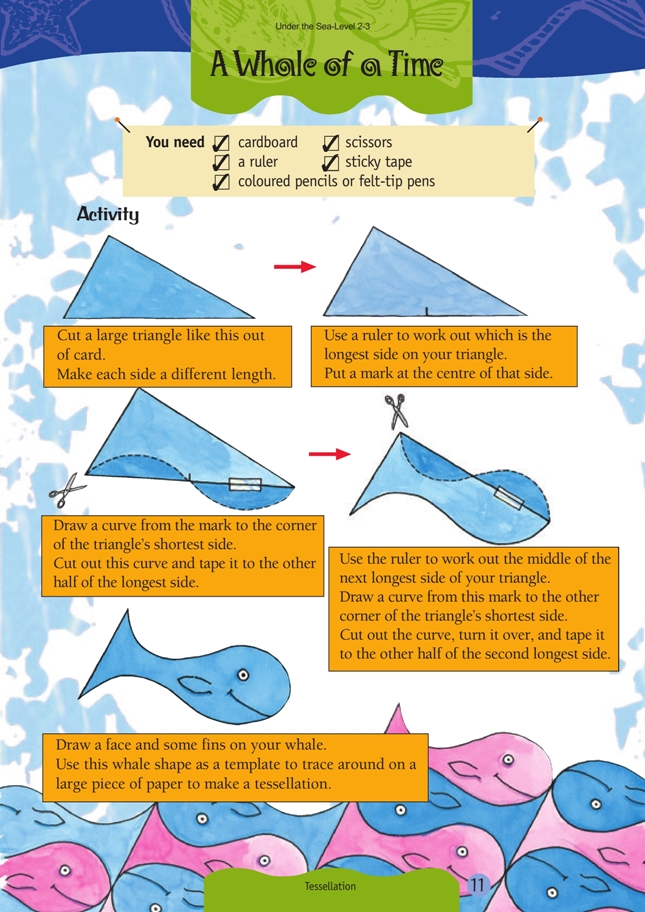
This is a level 2 geometry activity from the Figure It Out theme series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (294 KB)
make a tessellation pattern
FIO, Level 2-3, Theme: Under the Sea, A Whale of a Time, page 11
Coloured pencils or felt-tip pens
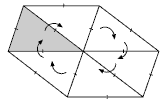
This tessellation activity uses a technique made famous by the Dutch artist, M.C. Escher. Since the internal angles of a triangle add to 180˚, any triangle can tessellate the plane by half-side rotation. For example:
This diagram shows the halfway point of each side of the triangle being used as the rotation point.
Note that each angle of the triangle is used twice about the central point, so 180˚ + 180˚ = 360˚ will complete a full turn.
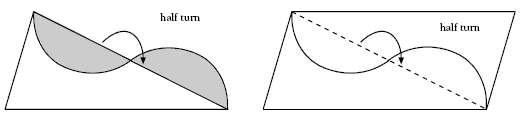
Since every triangle can tessellate by half-side rotation, it can be modified by the same process of halfside rotation and the tessellation will still hold:
When making their tessellating whale, students should mark the corners of their triangle before cutting. This helps considerably when tracing around the cardboard template to make the tessellation.
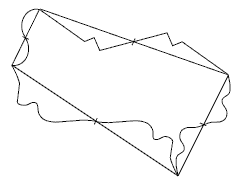
The half-side rotation technique also works for quadrilaterals and can be an excellent extension for capable students.
For example:
Since the angles of any quadrilateral add to 360˚, each angle of a
quadrilateral will be used once about a point.
Answers to Activity
Answers will vary.