Way to Go

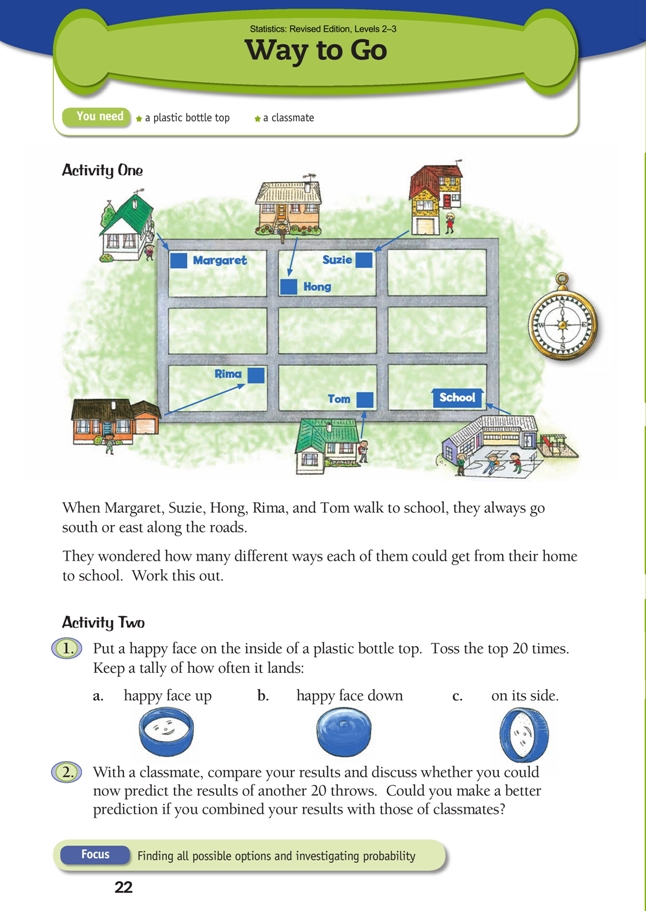
Activity One

Strictly speaking, this activity does not involve probability in that there is no random event: the decision to take one route to school, rather than another, is made on the basis of choice, not chance. This choice will be based on a matrix of factors that may include, for example, weather, friends, lateness, mood, transport, safety.
But there are many chance situations that can only be explored by fi rst setting out all the possible outcomes, and this activity gives students the opportunity to do this.
It is clear that Tom, who lives nearest the school, has only one south or east route he can take: east for one block. This route could be symbolised with a single arrow facing east (→).
Suzie’s routes all involve one easterly block and three southerly blocks. The four possibilities can be symbolised in this way: →↓↓↓, ↓→↓↓, ↓↓→↓, and ↓↓↓→.
Similar reasoning can be used to fi nd the number of routes for the other students:
Rima: →→↓, →↓→, and ↓→→ (three routes).
Hong: →→↓↓, ↓→↓→, ↓→→↓, →↓↓→, →↓→↓, ↓↓→→ (six routes).
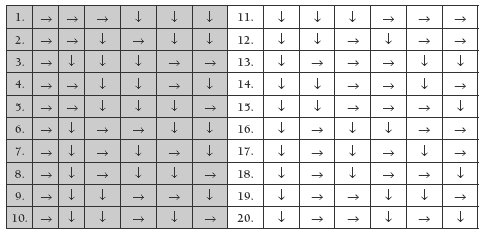
Most students will fi nd it a considerable challenge to write down all the possible routes for Margaret. They will need to be very systematic or they will have trouble working out which routes they have overlooked. There are 20 possibilities. If your students are up for the challenge, don’t tell them how many routes there are; let them try and work it out for themselves:

Note that, in the table above, the second 10 routes can be obtained simply by swapping east and south. This kind of symmetry can often be observed when listing all possible outcomes for a probability experiment.
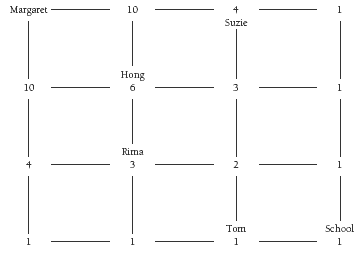
This diagram shows how many routes there are from each intersection:

The number at the top left-hand corner of a square is the number of possible routes to school.  It is found by adding together the numbers at the top-right and bottom-left corners of the same square. So Margaret has 10 + 10 = 20 different routes (see two halves of the table above) to school. You may recognise that the grid is in fact a rotated Pascal’s Triangle.

Activity Two

In the bottle-top throw, the only way to determine the likelihood of the outcomes is by trialling. This is because, unlike with a coin, there is no reason why a face-up and a face-down are equally likely and no way of theoretically determining the probability of an edge.
Encourage the students to record the results systematically in a tally chart. They are likely to find that the bottle top lands face up most of the time (due to the top’s centre of gravity) and that an edge, while not impossible, is very rare. The reasons for this would make a good discussion point.
You could suggest that students pool their results to obtain a larger data set. If they do this, they will be able to reach more definite conclusions about the probabilities of the three outcomes.
They should express these probabilities using numbers. For example, “You get a face-up about 12 times out of 20 trials.”

Answers to Activities

Activity One
The number of different ways for each student to walk from their home to school are: Tom (1), Rima (3), Suzie (4), Hong (6), and Margaret (20).
Activity Two
1.–2. Results and discussion will vary.

Key Competencies

Way to Go can be used to develop these key competencies:
• thinking
• using language, symbols, and texts.