This unit presents students with several problems that develop the idea of binary (base two) arithmetic. In the course of solving these problems, students look for patterns and relationships, and describe them using symbols and mathematical language.
- Use powers of two in problem situations.
- Find number patterns in practical situations.
- Experiment to find patterns.
In this unit we look at several problems, posed in a practical situation, that involve patterns related to powers of 2. The solutions to these problems may not initially appear obvious. Therefore, students should spend time exploring the problem by either acting it out or modelling it with the use of equipment. Although some of the problems presented may be very challenging for your students, this exploring, alongside the careful recording of thinking and results, should result in all students making some progress with each problem.
Central to these problems is the notion that any number can be written as the sum of distinct powers of 2. What’s more, each power of 2 that is used is used precisely once. Note that 1 is considered to be equal to 2 to the power zero. Hence 1 is a power of 2. Without this device, the first two statements of this paragraph are not true.
Having discovered this representation of numbers, and having realised that patterns have to be found, an amazing number of seemingly unrelated problems can be solved.
Links to Numeracy
This unit can be used to develop student knowledge of basic facts, in particular square numbers and their corresponding roots.
Students can create a list of known square numbers as they work with square numbers and their roots. Challenge students check the additions others have made.
What is the largest square number you can think of?
What is the smallest square number you can think of?
How can you check whether a number is a square number?
The learning opportunities in this unit can be differentiated by providing or removing support to students, and by varying the task requirements. Ways to support students include:
- providing extended opportunities for students to explore, and create their own problems involving, powers of 2
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities
- modelling the construction and use of diagrams in the solving of each problem
- allowing the use of calculators to aid in complex calculations and to avoid cognitive overload
- constructing a shared class chart of key ideas, expressions, and diagrams to be used by students as a point of reference
To increase the relevance of the learning in this unit, you might adapt the contexts presented in each problem. For example, the Fed Up Canteen problem could be adapted to include students lining up for a new or popular item (e.g. sneakers, concert tickets). Consider what contexts might be utilised here to make links to your students’ interests, cultural backgrounds, and to their learning from other curriculum areas.
Te reo Māori kupu such as ture (formula, rule), pū (exponent, indice, power), and tauira (pattern) could be introduced in this unit and used throughout other mathematical learning.
Getting Started
In this session, students explore numbers that can be obtained using powers of 2. They discover that, at most, one of each power of 2 is needed to make all numbers up to a certain amount.
Pose this problem for students:
Weka Post is a new company that can deliver your letters. They have a unique set of stamps which they believe allows you to put any exact amount of postage up to 63 cents which is their top letter rate. Here is the set of stamps.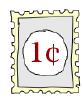





They also believe you need no more than one of each stamp to make any amount up to 63 cents. Are they right?
- Ask the students if they notice anything about the amounts shown on the stamps. Encourage students to notice that
- You double the amount on one stamp to get the amount on the next one
- The amounts shown are powers of two, 1 = 20, 2 = 21, 4 = 22, 8 = 23, 16 = 24 .
- Ask the students how letters that cost 13 cents and 25c could be stamped (8 + 4 + 1 and 16 + 8 + 1) and record these as examples. Tell the students that you want them to check out Weka Post’s stamping system and if their claim stands up. Expect students to have tried a large number of amounts or formed a generalisation about why the system works.
Allow the students a suitable period of time to explore this in co-operative groups then bring the class together to share ideas. Highlight the systematic ways in which students have recorded their results (e.g. lists, tables, diagrams).
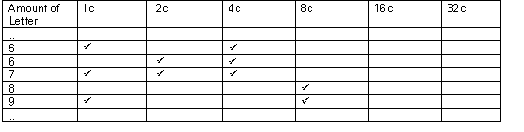
Some students may realise the system that is involved and come up with a generalisation like the following:
- With 1c and 2c you can make any amount up to 3c, so you add a 4c stamp. That means you can make any amount up to 7c by building on the 4c stamp (4 + 1, 4 + 2, 4 + 2 + 1). Then you add an 8c stamp. That means you can make any amount up to 15c by building on the 8c stamp (8 + 1, 8 + 2, 8 + 2 + 1, 8 + 4, 8 + 4 + 1, 8 + 4 + 2, 8 + 4 + 2 + 1). Then you add a 16c stamp which allows you to make any amount up to 31c, etc.
- Having validated that Weka Post’s claim stands up, pose this problem:
Weka Post want to move into the parcel market so they need to be able to stamp any letter or package up to an amount of $5.00. How many cents is that? If they were to extend their stamp system what new amounts of stamps would they need?The inclusion of 64c, 128c, and 256c stamps will allow them to display any amount of postage up to 511 cents ($5.11). How should they have discovered this?
Exploring
In this part of the unit, the students will get involved with two challenging problems that involve more aspects of powers of 2. The difficulty is to see the pattern that gives the answers. The first problem is an old one that you might get in a Christmas Cracker. The second one is harder but can be tackled by all of the class using counters. So all of the students can get something out of the lesson.
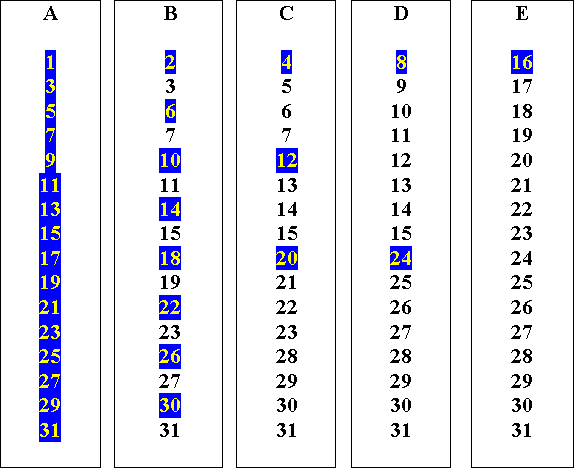
- Show the students the Think of a Number cards. Place them in a position so that all the students can see. Tell one student to choose any number from the cards and that you will guess what their mystery number is. Ask the student to tell you which cards their number is on, this will automatically tell you the number they have selected.
Suppose they choose the number 13 (unlucky for some but not for you!). It will appear on the cards in this way:
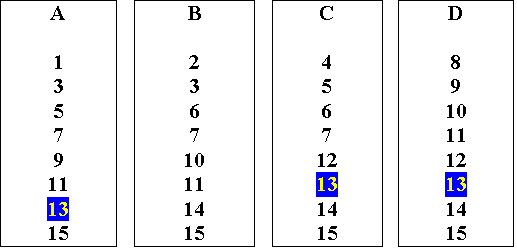
- The first numbers on these cards are the powers of two that make up thirteen. This is just like Weka Post’s stamps. All the numbers on the left hand card A have 1 (20) in their base two composition; the numbers on the centre left card B have 2 (21) in their composition; the middle right card C have 4 (22); and the right card D have 8 (23). So 13 = 1 + 4 + 8 = 20 + 22 + 23. So to determine the student's number all you need to do is to add the top numbers from the cards they named.
This works because each number from 1 to 15 is unique in its binary composition. If a student told you that their mystery number was on the A, B, and C cards you would know it was made up of 1 + 2 + 4 = 7, no other number has this composition.
Challenge the students by getting them to work out your mystery number that is on cards B, C and D (14 = 2 + 4 + 8).
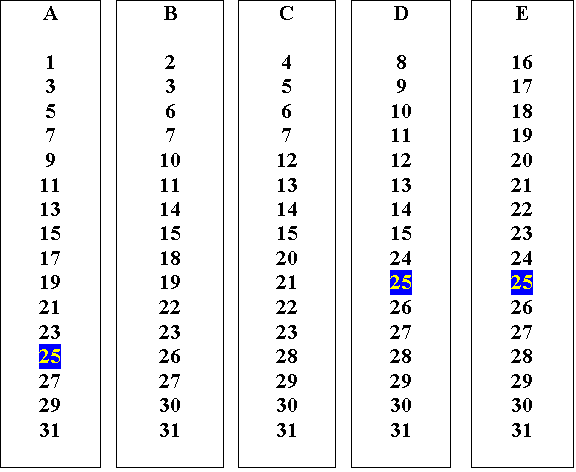
Tell the students to discuss in small groups how they think the cards were created and how they work. Then invite them to make a set of five cards that will work for all the numbers from 1 to 31. This set of cards will look like this with card E showing numbers that have 16 (24) in their composition and the previous cards A, B, C and D being extended as shown. So, twenty-five can be found on cards A, D, and E as it is composed of 1 + 8 + 16.
Tell the students the story of “The Grumpy Canteen Manager”. As you tell the story it is good to act out the scenario:
At the Fed Up Canteen there is a very grumpy manager. She makes THE most divine pies but is easily upset, particularly if students in line get restless and start to talk.
Let’s imagine that there are five students in line to be served and you are the fifth. (Get students up to the front of the class to be the students in line and one other to be the canteen manager.) To the first student she asks, “What do you want?” The student replies, “A pie please, Mrs Baker.” The first student gets served straight away (act out the first student being served and standing to the side of the line pretending to eat their pie). To the second student the canteen manager says, “You’ve been fiddling. Go to the back of the line!” (Act out the disgruntled second student going to the back of the line).
The service continues like this with the next (third) student being served a delicious pie straight away and the fourth being sent to the back of the line for fiddling. The fifth student is served. So if you are the last person in a line of five you will be the third person to get a pie.
Record this fact in a systematic way for the students, like a table or list:

Act out what would happen if there were six students in line to be served. Ask the students to predict when the last person will be served. The diagrams below show how this works, counters can be used to model the problem on an overhead projector:
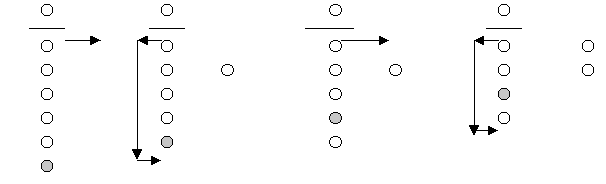
Student 1 is served Student 2 goes to back Student 3 gets served Student 4 goes to back
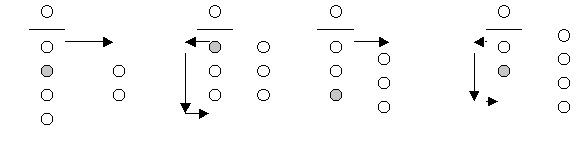
Student 5 gets served Student 6 goes to back Student 2 gets served Student 4 goes to back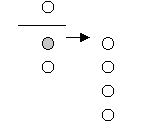
Student 6 gets served fifth.Add this new finding to the table of results:
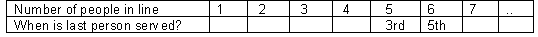
- Pose the problem for the students:
You are about to join the queue at the Fed Up Canteen. You know how many people there will be in line. Can you find a rule that will help you work out how long it will take for you to be served? The rule must work for any number of people in the queue. Allow the students to work co-operatively in groups of three or four. This will be necessary for them to quickly create enough results to look for a pattern. Encourage them to systematically record their findings.
- At different points in their deliberations the students will need to be brought together to process their ideas. They need to realise that this is a complex problem that will involve a lot of conjecturing, checking and rethinking.
Expect them to notice quickly that for an odd number of people the last person is served in the first run through of the queue.
So considering the odd numbers of people in the line these results occur:
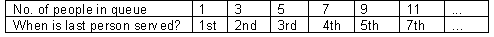
- Encourage the students to come up with a functional rule that will allow them to work out the order of the last person being served for any number of people in the queue. These rules might take the form of:
- “Add one to the number of people and divide by two. That gives the last person’s order, eg. (7 + 1) ÷ 2 = 4.”
- “Divide the number of people by two (halve it) and add one half, eg. (7 ÷2) + ½ = 4.”
You may wish to focus on why these rules give the same results. Bring out the Think of a Number cards and ask the students if they notice anything about which cards have all the odd numbers (they are all listed on card A). Ask why they think that this occurs. The other powers of two are even so unless a number has 1 (20) in its composition it cannot be odd since the sum of even numbers is always even.
- Refocus the students on the pattern when the queue has an even number of students. Here are some results that they should find by trialing with counters.
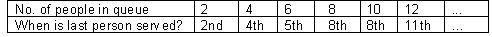
There doesn’t appear to be any pattern connecting the variables in this table but do not despair!
- Suggest to the students that this time they try a number like 16 in the queue and label each counter, the first person as one, the second as two, and so forth. This will allow them to keep track of the order in which the numbers get served.
- From the result with odd numbers we can see that they get served on the first pass through. You might model this with the counters. We know that these numbers are all on card A. Tell the students to carry out the second pass through of the queue and see which numbered people get served then. They will find that persons 2, 6, 10 and 14 get served. These numbers are the even numbers on card B. On the next pass, through persons 4 and 12 will be served. These are the person whose numbers are on card C and who are as yet unserved. On the fourth pass, person 8 is served (card D) followed by person 16 at last on card E.
Encourage the class to check this order with other even numbers of people in the queue and to look for patterns. Since each pass through involves division by two the binary (base two) composition of the numbers gives the order in which people will be served.
1st pass 2nd pass 3rd pass 4th pass 5th pass
Reflecting
Here is another problem with another pattern to find. You may not know the answer but you should strongly suspect that powers of 2 come into it somewhere. How is it related to what you have done so far?
- Students may enjoy solving a related problem called “Journey to the Sun.” Tell them this story:
Space Rockets Inc asked their astronauts to volunteer for the first space mission to land on the Sun. The astronauts were promised all sorts of incentives like a year’s supply of Iced Cola, super sun screen and designer swim wear. Still no person would volunteer. (I wonder why?)
So the manager decided to get tough and select the two astronauts for the mission in a fair and just manner. She gathered all her space staff in the reception room and told them this: “In the room next door I have exactly the right number of seats for you all. They are numbered from one to twenty. I will ask you to choose a seat when you go in. Then I will start at seat one and say, ”You may go”, to seat two, “Stay”, to seat three, “You may go,” to seat four, “Stay” and so forth. I will continue telling every second remaining astronaut to leave until only one person remains. They will be the lucky person to fly the first manned or womanned space mission to the sun.”
The astronauts were less than enthusiastic but accepted that their chances of being picked were quite slim. One smart astronaut boasted, “I know which seat not to sit in”.
- What rule could the astronaut possibly have to work that out so quickly, especially seeing as she had just found out how many seats would be there?
- Students should either act out the problem, with several different numbers of astronauts seated, or use diagrams. Remind them before they begin work that the astronauts do not know beforehand how many of them will be present so the rule will have to be a general one which applies to any number of seats
The table of results will look like this:

Students may notice that on powers of two the last seat number is the total number of astronauts. What’s more, the last seat is always even – and increasing. Well, almost always increasing. When does it stop increasing? This allows a rule that works from the power of two below the number of astronauts present. For example, suppose there were 19 astronauts. For 16 astronauts seat 16 would be the last chosen, that means that for 17 astronauts seat 2 would be it, 18 would be 4 and 19 astronauts would mean that seat 6 would be the wrong place to be! This is because 2, 4, 6 are the even numbers in order starting from 17.
- Isn’t this just the Fed Up Canteen problem in disguise? Just look at that problem a slightly different way. But why do the answers really work?
Dear families and whānau,
Recently we have been exploring number patterns, especially those related to powers of 2, in problem and practical situations. Ask your child to share their learning with you.