This unit uses tukutuku panel designs as a context for developing algebraic thinking, especially quadratic relationships. The context allows students to solve problems using tables of values and algebraic formulae.
- Find the number of crosses in tukutuku panels figuratively by using the area of squares and rectangles.
- Find the number of crosses in repeating tukutuku panels by using linear and quadratic formulae.
Triangular numbers and patiki patterns are used as a powerful way to introduce patterns, and can lead to the application of quadratic and linear formulae. A number of alternative geometric views are suggested. Establishing that the formulae are identical is a useful application of quadratic algebra skills.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- modelling the mathematical processes involved in each stage of the unit
- using supportive tools, especially tables of values, so students can notice patterns and take progressive steps to generalisation
- focusing on the figurative (spatial) structure of patterns as well as on the numeric patterns. Figures can be structured in ways that lead naturally to generalisation for the nth term
- providing opportunities for students to revisit, explore, and build patterns in small groups, as individuals, and alongside the teacher
- providing opportunities for students to develop and explore new patterns using blocks and tables
- allowing students to use materials when building patterns
- allowing the use of calculators to avoid cognitive overload
- encouraging students to work in collaborative groups to develop explanation and justification strategies. Strategically organising these groups allows for greater peer learning, scaffolding, and extension
- varying the size of the terms that students work with, bearing in mind that larger terms require students to think in functional rather than recursive ways.
The context for this unit is tukutuku panels that can be found in wharenui on marae. The panels symbolise the mana of the ancestor embodied in the house. Other situations of relevance to your students might also be used to develop the same kind of thinking. Examples might be stacking arrangements in trays, designs on tapa cloth, decorative arrangements of plants, and patterns found in the arrangements of hole in gameboards, like ludo.
Te reo Māori kupu such as tauira (pattern) and ture (formula, rule) could be introduced in this unit and used throughout other mathematical learning.
Session 1
- Explain to students that tukutuku panels are made from crossed weaving patterns.
Here is a sequence of the first four triangular (tapatoru) number patterns.
Either provide Copymaster One or get students to build the designs with square tiles.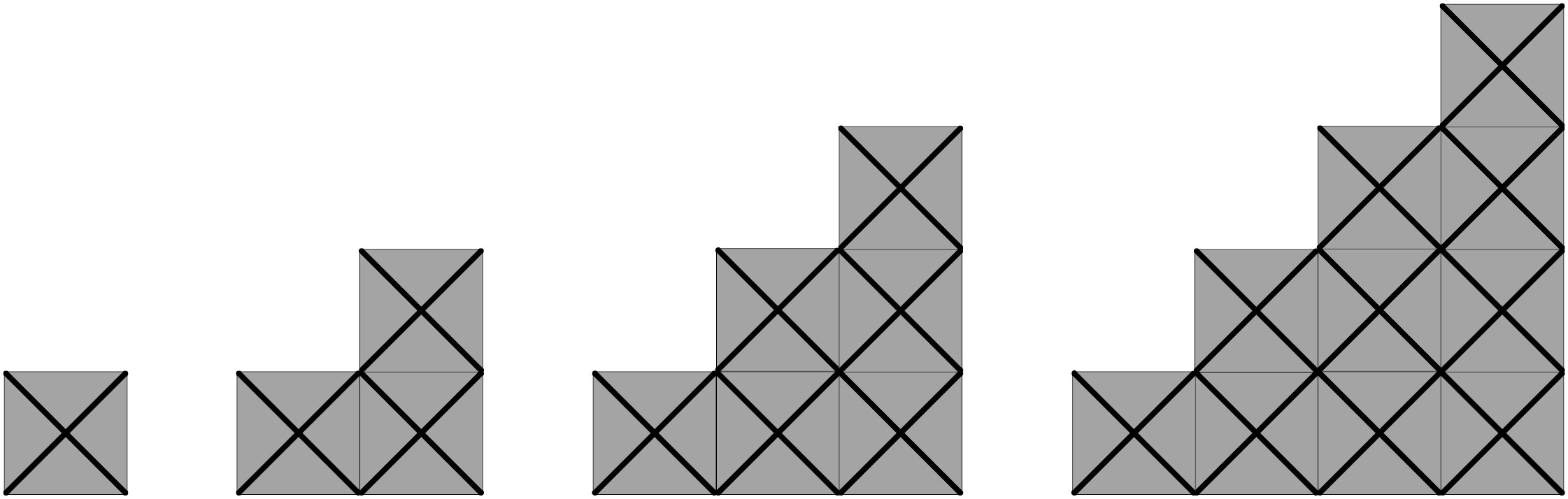
How many squares make up each term in the sequence?
Is there a pattern that allows you to predict the number of squares in the fifth pattern? Build up a table of values to support students look for a pattern.
Term (Tn) 1 2 3 4 Number of squares 1 3 6 10 - Using the table, work together as a class to predict terms 5 and 6. Students may develop recursive rules that focus on working with a term to get the next. For example, they may notice that the differences increase by 1, 2, 3, and 4, and anticipate this growth pattern will continue.
Suppose you had to find the 25th term. How would you do that?
Students should notice that the recursive method is very cumbersome for larger terms.
- Ask students to add the same shapes in a different colour that have been rotated 180 degrees (shown on Copymaster 1). Two triangles form a rectangle that is easier to work with.

- Discuss how to find the number of crosses in the fifth member of this sequence by looking at the developing structure. (6 rows of 5 = 30.)
You might add a row to the previous table:
Term (Tn) 1 2 3 4 Number of squares (triangles) 1 3 6 10 Number of squares (rectangles) 2 6 12 20 What do you notice?
Encourage students to note that the number of squares for the triangles is half that for the rectangles.
How can you find the size of the rectangle from the term number?
Connecting the visual pattern with each term produces rectangles that are 1 x 2, 2 x 3, 3 x 4, 4 x 5,…Encourage students to notice that one factor is the term number and the other factor is one more.- Discuss what the fifth and sixth rectangular and triangular number are. (5 x 6 = 30, 30 ÷ 2 = 15 gives the fifth terms, and 6 x 7 – 42, 42 ÷ 2 = 21 gives the sixth terms.)
- Discuss what the 1000th triangular number is. (1000 x 1001 ÷ 2 = 500 500.)
- Generalise to the nth triangular number is. (n(n+1)/2)
- Let T4 stand for the 4th triangular number, and S4 stand for the 4th square number.
- Discuss why S4=T4+T3 from the drawing. (Shown on Copymaster 1.)
- Get students to draw/make a picture that shows why S5=T5+T4.
Together, construct a table of values for triangular numbers using the formula n(n+1)/2.
n 10 11 12 13 14 15 16 17 Tn 1 3 6 - Check from this table, for a variety of values of n, that Sn=Tn+Tn-1.
- Explain geometrically why Sn=Tn+Tn-1.
Challenge:
Show that Sn=Tn+Tn-1 by using algebra.
![]()
Session 2
Patiki (flounder) patterns.
Present students with this sequence of Patiki patterns. This is shown on Copymaster 2.
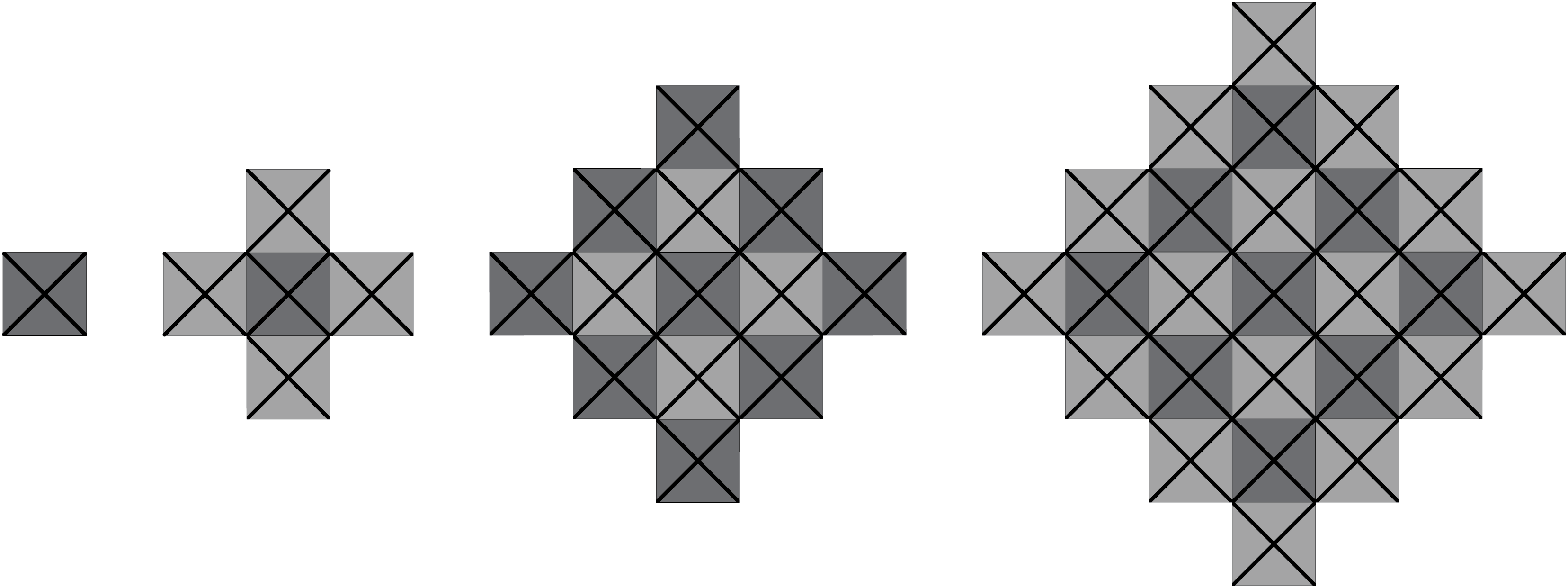
- Discuss how the shading helps us to recognise that in the fourth pattern that there are 4 diagonal lines of four grey crosses, and 3 diagonal lines of 3 black crosses. Therefore, there are 4 x 4 + 3 x 3 = 25 crosses altogether.
- Have students apply this reasoning to the third pattern to see there are 3 diagonal of 3 black crosses and 2 diagonal rows of 2 grey crosses = 13 crosses.
- Using the same reasoning, discuss how many crosses the fifth patiki pattern will need. (5 x 5 + 4 x 4 or 52 + 42= 41).
- Have students find the number of crosses needed for the 100th patiki pattern. (1002 + 992= 19 801), and the nth patiki pattern (n2+(n-1)2)
- Use another geometric method:
The fourth patiki pattern is shaded in a new way. This is shown on Copymaster 2
- Discuss how the top half shows S4=T4+T3 when the grey T3 is rotated around to fit.
- Discuss how the bottom half shows S3=T3+T2 when the black T2 is rotated around to fit.
- If P4 is the number of crosses in the 4th patiki pattern discuss how all this shows P4=S4+S3=42+32=25.
- Discuss why P100=S100+S99=1002+992=19 801.
- Draw the 5th patiki pattern using this shading and explain how this shows that the 5th patiki number is 52+42.
- Explain how this reasoning shows the nth patiki number is Pn=n2+(n-1)2.
- Use algebra to show that Pn=2n2-2n+1.
Session 3
Another way to find the formula for Pn is found.
- Show the picture of the 4th patiki pattern (grey) surrounded by four T3 shapes. This is shown on Copymaster 3. Tiles can be used to make an S7.

- Explain how this shows P4=S7-4T3.
- Draw a picture, or use tiles that show why P3=S5-4T2.
- Complete the pattern in the formulae:
P3=S5-4T2 P4=S7-4T3 P5=S9-4T4 P6= ______
Pn= ______
(Answer: Pn=S2n-1-4Tn-1.)
Hard: Use Pn=S2n-1-4Tn-1 to show: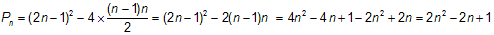
Session 4
A string of 5 patterns based on the 3rd triangular number is shown (Copymaster 4). Shading has been added to assist working the number of squares in the pattern.

- Let students find a way to structure the figure to count the number of squares. Students may notice that the pattern is made of overlapping triangular numbers. The overlaps mean that 6 x T4 is more than the total of squares. There are four overlaps.
- Students might also recognise that the pattern begins with T4 and adds on five squares for each additional section.
Discuss why the total number of squares for Term 5 (Five sections) is both:
6 + 4 x 5 = 26 and 5 x 6 - 4 = 26. - If this pattern were repeated to 1000 sections what is the number of squares needed? (6 + 999 x 5 or 1000 x 5 + 1.)
- If this pattern were repeated m times what is the number of squares needed? (16+5(m-1) or 5m+1.)
Show a string of four triangular patterns (shown on Copymaster 4).

- How many squares are needed to make the 100th pattern?
(Likely answers: 10 + 99 x 9 or 100 x 9 - How many squares are needed to make the mth pattern?
- (Likely answers: 10 + 9(m - 1) or 9(m + 1.)
- Develop or present a general rule:
If the nth triangular pattern is repeated m times how many squares are needed?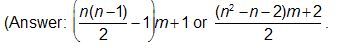
Session 5
A string of six patiki patterns is shown (Copymaster 5). It is based on repeating the 3rd patiki pattern. Shading has been added to assist working the number of squares in the pattern.
- Knowing that P3=32+22=13 discuss why the number of squares is 13 + 5 x 12 or
6 x 12 + 1. - If this patiki pattern were repeated 100 times what is the number of squares needed?
(13 + 99 x 12 or 100 x 12 + 1 which is 1201.) - If this patiki pattern were repeated m times what is the number of squares needed?
(13+12(m-1) and 12m+1.) - Are 13+12(m-1) and 12m+1 the same? Demonstrate that they are the same by algebra.
- Repeat for a string of four patiki patterns (Copymaster 5) This pattern is based on repeating the fourth patiki pattern.

- Find the number of squares for the 100th pattern. (P4=42+32=25, so the 100th pattern needs 25 + 99 x 24 or 100 x 24 + 1 = 2401.)
- Find the number of squares for the mth pattern. (P4=42+32=25, so the number of squares is 25+24(m-1) or 24m+1.)
- Repeat for patterns based on other sizes of patiki patterns.
Dear families and whānau,
We have been investigating the number of crosses in tukutuku panels figuratively by using the area of squares and rectangles, and have been using linear and quadratic formulae to find the number of crosses in repeating tukutuku panels. Ask your child to tell you about the tukutuku pattern below, and how a table, area, or algebra might be used to predict a future term in the pattern.
