This unit explores some of the algebra involving triangular and square numbers.
- Classify numbers as triangular or square numbers.
- Find general rules for the triangular and square numbers.
- Apply triangular and square numbers to solve problems.
Triangular and square numbers belong to a family called the figurative numbers. These arise from shapes formed by particular numbers of objects. Figurative numbers are believed to have originated from the Pythagorean society of ancient Greece (c. 550-350 BC).
Both triangular and square numbers occur frequently. Triangular numbers commonly arise in probabilistic situations, most notably in establishing the number of combinations for a set of objects. Square numbers are the simplest example of a quadratic function. Quadratic functions are used frequently to model real world situations, such as paths of balls in sport, braking distance of cars, and structures of suspension bridges.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- checking students’ prior knowledge of triangular and square numbers and the mathematical language related to this
- working with calculators to reduce the burden of calculation and concentrate on generalisation.
- using physical and diagrammatic representations before representing the patterns symbolically.
- using supportive tools, such as tables, to support students to look for patterns.
- encouraging students to progress from additive (recursive) thinking with tables to multiplicative (functional) thinking through amplifying problem difficulty and asking anticipatory questions.
- applying figurative and arithmetic thinking to patterns to capitalise on students’ strengths
- using digital devices to record and share students' thinking, justifications and reflections.
The context for this unit is the figurative numbers formed by triangles and squares. The formations are commonly used in pursuits like marching, quilt, and lino design, and stacking items for display. Fish swim in schools and geese fly in flocks that resemble triangles and plants and cars are often laid out in arrays. Choose contexts that are meaningful to your students and feature triangles and squares as common patterns.
Session 1
Triangular Numbers
- Show the students slides one and two of PowerPoint One. Students are asked if the stacks contain the same number of cubes and how they counted the cubes. Ask students to share their methods with a partner.
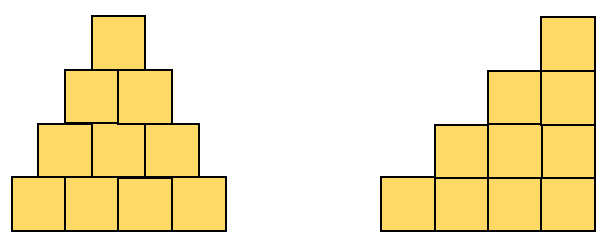
- As a class, discuss the methods used (for example, adding the layers. 1 + 2 + 3 + 4 = 10.)
Explain that ten is a triangular number since it forms a triangular pattern.
Ten equals five multiplied by two (write 2 x 5 = 10).
Can you see two times fives in the stack somewhere? - Challenge the students to draw or create a triangular stack that is five cubes high.
How many cubes are in the fifth biggest triangle?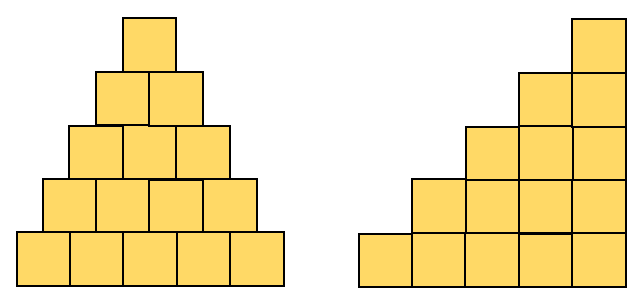
- Slide Four has the fifth triangular arrangement. Students may just add five to the original four-high triangle. You might record the sum of the layers as 1 + 2 + 3 + 4 + 5 = 15.
Will the ten-high triangle have 30 cubes? - Let the students discuss the question in pairs. Since the growth is not linear (different numbers of cubes added for each layer) the number of cubes in triangle ten will be more than 30.
Find how many cubes would be needed to make the tenth triangular number, that is a triangular pattern that is ten-high?
Allow the students access to cubes or counters if needed. Encourage them to work towards using mental arithmetic to find a solution. Discuss ways in which they solved the problem.
Students are likely to repeatedly add layers; 1 + 2 + 3 + 4 + 5 + 6 + 7 +8 +9 + 10 = 55. Others may note that forming tens is useful, for example. (1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 10 + 5 = 55. - Show Slide Five which animates the fourth triangular number being transformed into 2 x 5 = 10.
Ask students to discuss: How are the rows of five made?
1 + 2 + 3 + 4 = (1 + 4) + (2 + 3)
= 2 × 5
= 10 - Encourage the students to use the same forming pairs strategy for the tenth pattern.
Let the students use cubes or counters to show how the tenth triangle can be transformed into a rectangle. Slide Six shows the transformation as an animation.
(1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = 5 × 11
= 55 - Challenge the students to make up a list of the triangular numbers for as far as they can, beginning with the known numbers; 1, 3, 6, 10, 15, …, 55, …
- Discuss what patterns they can see that would allow them to work out the next number without making the figure with counters. Provide cubes and counters for students to use - either to calculate the pattern or confirm their thinking. Ask students to share their ideas with a partner. Note that the pattern goes:

- Slide Seven tells the story of Carl Frederick Gauss when he was a child aged ten. You can find excellent videos of the story online by searching “Gauss addition”. Stop the video before Gauss’s method is shown.
How is adding the numbers 1-100 the same as finding the number of cubes in a triangle 100-high?
Give students time to discuss their ideas and justifications. - Challenge the students to find the 100th triangular number, i.e. the sum of the counting numbers to 100:
1 + 2 + 3 +… + 98 + 99 + 100 = (1 + 100) + (2 + 99) + (3 + 98) + …
= 50 × 101
= 5050
Square Numbers
- Use Slides Eight and Nine to introduce the pattern of square numbers. For each picture on Slide Eight, ask your students to work out the total number of objects.

Students should notice that each picture shows a square number of objects.
What is the quickest way to count the number of objects in each picture?
Do your students recognise that multiplication can be used to shorten repeated addition? - Record each pattern like this:
5 x 5 = 52 = 25 6 x 6 = 62 = 36 8 x 8 = 82 = 64 - Show that 52 means “five squared” as it represents the area of square with sides of five units in length. Challenge your students to find other square numbers. Compile a collective list as more square numbers are found. Slide Ten animates the creation of the first five square numbers. Note that the differences between consecutive square numbers are all odd.
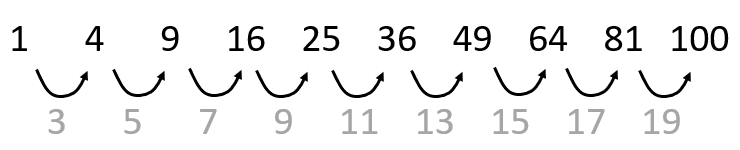
Why are the differences always odd numbers?
Allow individual thinking time, then time for a discussion with a buddy or small group. - Slide Eleven animates the fact that the differences between consecutive square numbers is always a multiple of two plus one. Since odd numbers are always an even number plus one, the difference is always an odd number.
- Slide Twelve shows a 7 x 7 jigsaw.
- Challenge the students to find the 100th square number which is 100 × 100 = 1002 = 10 000.
Session 2
- Revisit the set of triangular numbers. PowerPoint Two, Slides One and Two, introduces an investigation. Ensure that students know the meaning of consecutive as ‘next to each other.’
- Ask the students to find the sum of consecutive triangular numbers up to ten, and organise their results in a systematic way. For example:

- Ask the students to describe any pattern they see and record it as a claim. For example:
Claim One: “If you add any two consecutive triangular numbers, the sums go even, odd, even, odd,...”
Claim Two: “If you add any two consecutive triangular numbers, the sum is always a square number.” - Suggest to the students that they need to come up with a way to convince others that their conjecture (a statement that has not yet been proved true or false) is true. Their arguments might use specific examples but should be generalisable across all cases.
Claim One: Triangular numbers go in this pattern:
1 3 6 10 15 21 28 36 45 55 ... odd odd even even odd odd even even odd odd ... “I know that an odd number plus an odd number gives an even sum. I know that an even number plus an even number gives an even sum. I can look at the sums of consecutive triangular numbers like this:”
1 3 6 10 15 21 ... odd odd even even odd odd ... sum even odd even odd even ... “The sums will cycle like that forever [infinitely]. If I start on an odd triangular number, the sums will be either even, odd, even, … or odd, even, odd, … The same happens if I start on any even triangular number.”
Note that this argument is based on induction, the idea that if a pattern for a sequence holds true, it can be generalised infinitely to further members of the sequence.- Claim Two: Triangular numbers of objects can be arranged as right angled triangles. If you put two consecutive triangles together they form a square.
Students usually start with observations, that every pair of consecutive triangular numbers they try sum to a square number. They may provide an extensive list to show this, hopefully using a spreadsheet.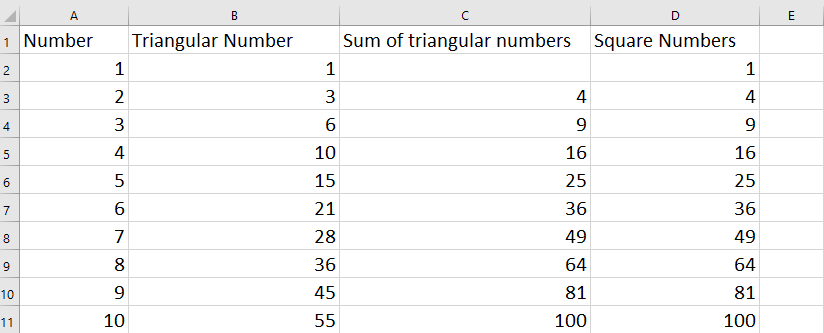
In mathematics, a large set of results suggests a relationship holds, but is not conclusive proof. Only one counter-example is needed to show the relationship is not generalisable. To prove the sum of two consecutive triangular numbers is always a square number algebraically requires techniques taught at Levels 5 and 6. However, a geometric proof is very accessible. - Slides Three, Four and Five of PowerPoint Two show examples of representing the sum of triangular numbers geometrically. For example:
This may lead to the generalisation of what occurs for any pair of consecutive triangular numbers. - Slide Six shows the process for any triangular number, ∆n+∆n+1.
Require the students to be more specific in terms of expressing their generalisation.
If you know the value of n for the first triangular number, e.g. ∆n=∆10, can you predict the sum (square number)? - Use specific examples, to encourage students to describe the link between triangular numbers and square numbers, e.g. 10 + 15 = 25 so ∆4+∆5=52. Ask them to express their ideas in words and symbols, such as:
"If the triangular numbers are the tenth and eleventh, then the sum equals eleven squared."
A set of results may help students see the general pattern.
∆3+∆4=42
∆6+∆7=72
∆10+∆11=112
…
∆n+∆n+1=(n+1)2 - Slides Six and Seven provide some problems where a square array is divided into consecutive triangular numbers.
Try to figure out the number of dots in each red and yellow triangle, using the information, and your list of triangular numbers. Try not to count dots.
To solve the problems efficiently students will need to find the square root of the total number of dots. For example, √256=16. Students may not be familiar with the square root function on their calculator. If they know the square number, e.g. 16th square, they can look up the nth and (n-1)th triangular numbers, e.g. ∆16=136 and ∆15=120. Ask them to do a final check to ensure the two triangular numbers add to the square number.
Session Three
Square Numbers
- Use Copymaster 1 to provide the students with a sequence of problems related to square numbers. Allow the students to solve the problems independently or in small co-operative groups. Assemble the class to discuss the common features of the problems.
Problems one and two both contain geometric patterns in which an odd number of triangles or squares is added to the previous pattern. Consideration of the layers in the triangular pattern shows that one, then three, then five, then seven triangles are added. This is the property of the sequence of square numbers found in lessons one and two. Students should realise that the tenth square number is 100 so the large triangle would have sides of ten units.
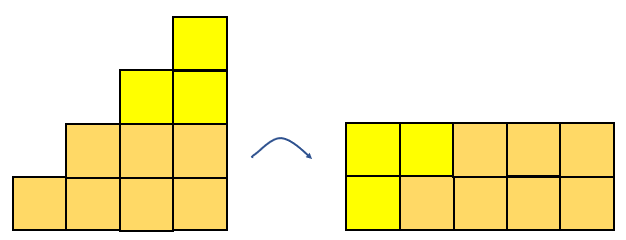
Similarly, rearranging the staircase patterns shows that they can be reformed into squares. For example, here is a reformation of the 4-high staircase.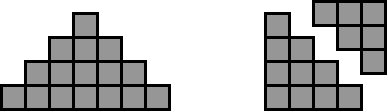
The number of small squares found in a 15-high staircase would be the fifteenth square number (15 x 15 = 225). - The garden problem (Problem Three) also involves square numbers, as students should detect from the 36m2 and 64m2 square fields. The problem requires connections to the square root, that is the side length that produces a square of given area. So the length of a side in the 49m2 plot is 7 metres since √49=7.
Comparing the side lengths of the given squares 6 metres and 8 metres suggests that the small plot adjacent to them must have a side length of 2 metres (area 4m2). By working systematically students should get to this solution.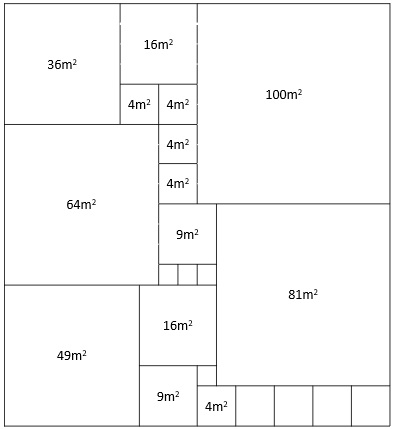
- In Problem Four students should recognise similar number sequences in the “Dance till You Drop” competition. If someone dances for twenty-four hours the last hour will be worth $47 and they will receive a total of 242 (twenty-four squared) dollars. That is $576.
For problem Five students will need to be aware that there are different sized squares involved. This is helpful in systematically finding them all. Consider the 4 x 4 checkerboard.
Counters can be used to mark the centre of each square as shown below.
…and the large square itself.
So the 3 × 3 checkerboard has 1 + 4 + 9 + 16 = 30 squares (The sum of the first four square numbers) By similar reasoning the 8 × 8 checkerboard will have 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 = 204 different squares. - The same reasoning used in Problem Four can be used to work out the total distance. Since the sum of consecutive odd numbers the distance to each cone is always a square number:
Cone A is 1 metre from the start
Cone B is 1 + 3 = 4 metres from the start
Cone C is 1 + 3 + 5 = 9 metres from the start
Etc.
To complete the whole exercise the player dribbles 2 x (1 + 4 + 9 + 16 + 25 + 36) = 182 metres.
Triangular Numbers
- Give the students copies of Copymaster Two that has problems related to triangular numbers. Allow them to solve the problems individually or in co-operative groups (mahi tahi).
- After a while gather the class together to share their solution strategies.
- In solving problem one the students might note that the welds form matching triangular patterns allowing the triangular numbers to be used in an efficient way to get the answer. For example, the welds for four joined squares is twice the third triangular number (2 x 6 = 12). For ten squares twice the ninth triangular number, forty-five, gives the number of welds (2 x 45 = 90).

- Problem two involves a pattern in which the next distance in the spiral is the previous distance plus one metre. Students should recognise that this pattern of differences is found in the triangular numbers. Since the last ‘leg’ of the spiral is 14 cm long, they should look for the 14th triangular number which is 105 cm.
- This pattern is less recognisable in problems three and four that involve combinations. In the ice cream problem each new flavour creates an extra number of ice creams equal to the previous number of flavours plus one. For example, combining Uncool with the other flavours X, Y, and Z, gives four more possible ice creams. They are XU, YU, ZU, and UU. The next flavour Vex will combine with the others to create five more double scoop icecreams XV, YV, ZV, UV, and VV. The total number of possible icecreams will be the sum of 1 + 2 + 3 + 4 + 5 + 6 = 21 (the sixth triangular number).
- Similar reasoning can be used to solve the other two problems. Each new town creates the need for a number of roads that is equal to the number of existing towns. Consider the addition of the first new town, Dag, results in three new roads, AD, BD, and CD.
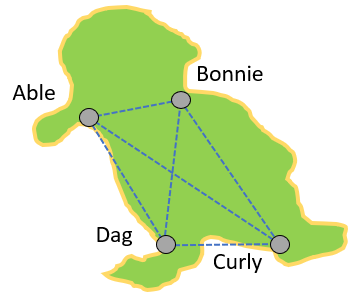
So the number of roads with seven towns in total will be the sum of 1 + 2 + 3 + 4 + 5 + 6 = 21 (the sixth triangular number). - Problem Five involves a different context but the same mathematics where each new person added must play games with each of the current players. The number of games that must be played is the sum of 1 + 2 + 3 + …+7 + 8 + 9. This is forty-five, the ninth triangular number.
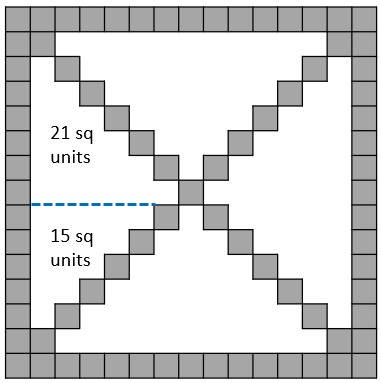
- Problem Six is a geometric application of triangular and square numbers. There are four identical white spaces that are stairs. Each stair can be partitioned into two triangles which can also be remembered as forming a square. 15 + 21 = 36, the sixth triangular number. There are four empty spaces so the area not shaded equals 4 x 36 = 144, which is also a square number.
Session Four
In this session students apply their knowledge of triangular and square numbers to solve problems with sequences. PowerPoint Three drives the lesson.
- The first sequence of problems is aimed at students creating a general rule for triangular numbers. Show Slide One. Invite your students to find out how many apples are in the rectangular stack. Share their ideas.
- Slides Two and Three show two ways to solve the problem, by multiplication of sides, and by partitioning into triangular numbers. Slides Four to Six provides a simpler example, 5 x 6 = 30 in total, 2 x 15 = 30 (two times a triangular number).
- Slide Seven requires the students to identify the number of apples in each triangle. The total number in the array is 11 x 12 = 132 apples. Each triangle is half of that total, 132 ÷ 2 = 66.
- Let your students work in small groups on Slides Eight, Nine and Ten. Encourage discussion and justification. Solutions are below.
Triangular stack

This pattern is the set of triangular numbers. The table of values is:
From the first slides the students should recognise that two copies of a triangular arrangement combine to form a rectangle. For example, two copies of the fourth triangle form a 5 x 4 = 20 rectangle. In general, two copies of the nth triangle form a n x (n + 1) rectangle. In reverse, to find the nth triangular number divide n x (n + 1) by two.
- The 25th triangular number equals 25×26÷2 or (25×26)/2 = 325.
- The nth triangular number is given by the formula n(n+1)/2 = ∆n.
- To find the number of apples wide (n) then solve n(n+1)/2 = 210. An easy way to do that is to estimate which two consecutive whole numbers multiply to 420. 20 x 21 = 420 so n must be 20.
House-shaped stack

Students might partition the figures in various ways to solve the problems. One way is to separate the figures into square and triangular numbers.
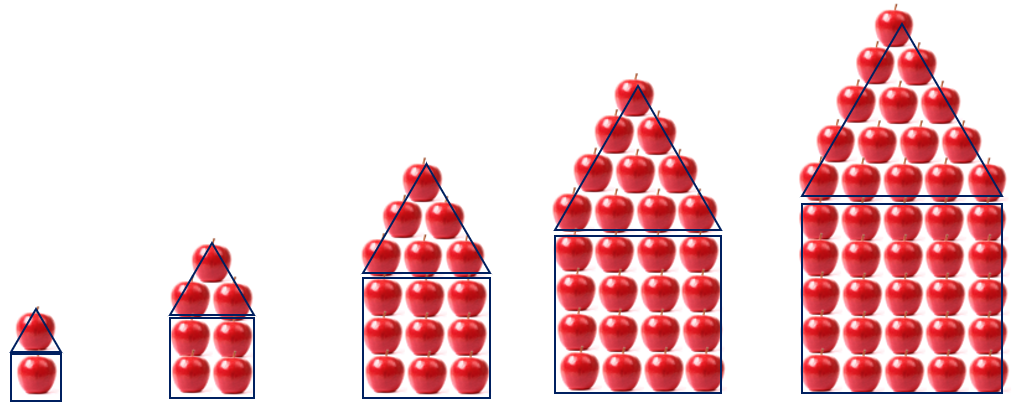
- If the figure is the nth square number plus the nth triangular number, then the 25th figure is made of 252+(25×26)/2 = 625+325 = 950 apples.
- In general, the nth figure is made of n2+n(n+1)/2 apples. Advanced students may like to simplify the expression to (3n2+n)/2 but those skills are expected at Level Six of the New Zealand Curriculum.
Greek Cross Array
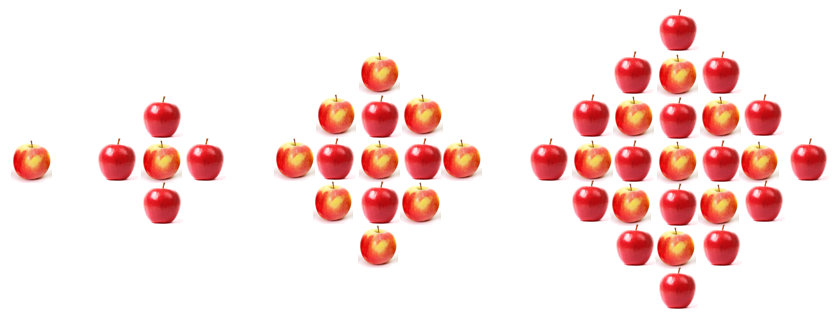
- Each figure is made up of a square array of red apples, and a square array of golden apples. The 25 apple-across figure is made of 252 +242= 1201 apples. 625 apples will be golden and 576 will be red.
- In general, the nth figure is made up of n2+(n-1)2. To find out the figure that is made from 761 apples solve n2+(n-1)2.= 761. The easiest way to do that is to look for two consecutive square numbers that add to 761. Twenty is a good start since 202=400. Try 202+192=761. The figure is 20 apples along each side.
Final Challenge
As a final problem pose this challenge (See Slide Eleven):
What is the smallest number of apples that need to be moved to change this triangular pattern into a square pattern?
Students could record their ideas and explain their thinking in a digital format so they can share with their family and whānau.

This triangular pattern can be changed into a square by moving only a few apples.
Students may realise that the figure has 36 apples that could be used to form a 6 x 6 square pattern.
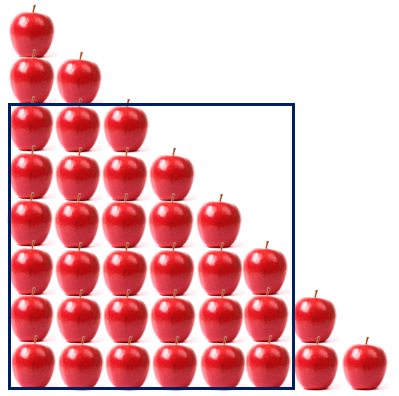
Superimposing the size of a 6 x 6 counter square over the triangular array reveals that only six apples need to be moved.
Students can write or record a reflection about their learning. Encourage them to record what they learnt and what further learning they think they need to do.
Dear family and whānau,
We have been exploring square and triangular numbers. Ask your child to share and explain their final task, relating to apples. They can also share some of their learning and tasks from throughout the week. Ask your child to explain their knowledge of square numbers.