This problem solving activity has a number and algebra (equations and expressions) focus.
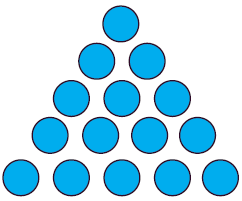
Mary knows that the 5th triangular number is 15 because it needs 15 counters to make the triangle.
But she doesn’t know which of these expressions is equal to the nth triangular number, T(n).
Which are and which aren’t and why?
(1) T(n) = 1 + 2 + 3 + 4 + . . . + (n – 3) + (n – 2) + (n – 1) + n;
(2) T(n) = ½n(n + 1);
(3) T(n) = 1 + 3 + 5 + … + (2n – 5) + (2n – 3) + (2n – 1).
(4) T(n) = n2 – (n – 1)2 + (n – 2)2 – (n – 3)2 + . . . + 42 - 32 + 22 – 12;
(5) T(n) = [(n + 1)2 + n2 + (n – 1)2 + ... + 12] – [(n2 + 2) + ((n – 1)2 + 2) + ((n – 2)2 + 2) + … + (12 + 2) + 2];
(6) T(n) = T(n -1) + n and T(1) = 1.
- Use algebra to simplify expressions.
- Use geometry to assist with algebraic calculations.
This problem involves students recognising and continuing the pattern of triangular numbers and finding the algebraic formula for the nth triangular number (the general term of the pattern).
This is the last of four related problems: Triangular Numbers, Number, Level 3; Counting Pills, Number, Level 4; and Square and Triangular Numbers, Algebra, Levels 5.
The Problem
Mary knows that the 5th triangular number is 15 because it needs 15 counters to make the triangle.
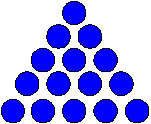
But she doesn’t know which of these expressions is equal to the nth triangular number, T(n). Which are and which aren’t and why?
(1) T(n) = 1 + 2 + 3 + 4 + . . . + (n – 3) + (n – 2) + (n – 1) + n;
(2) T(n) = ½n(n + 1);
(3) T(n) = 1 + 3 + 5 + … + (2n – 5) + (2n – 3) + (2n – 1).
(4) T(n) = n2 – (n – 1)2 + (n – 2)2 – (n – 3)2 + . . . + 42 - 32 + 22 – 12;
(5) T(n) = [(n + 1)2 + n2 + (n – 1)2 + ... + 12] – [(n2 + 2) + ((n – 1)2 + 2) + ((n – 2)2 + 2) + … + (12 + 2) + 2];
(6) T(n) = T(n -1) + n and T(1) = 1.
Teaching Sequence
- Introduce the problem to the class.
- Brainstorm ideas for approaching each part of the problem.
- As the students work on the problem, you might ask the following questions to extend their thinking:
What strategies might help you to find the answer?
How can you use your knowledge about algebra here?
Can you see any patterns that might help?
How does your geometric knowledge help? - Share the students’ answers. Have them explain their reasoning. Talk about what is needed to write down a complete solution to the problem.
- Have students write up their method of solution. Check that they have correctly used the main ideas of the argument.
- Encourage students to work on the extension problem. It can be done in conjunction with the original problem.
- Discuss the extension problem with the whole class. Have them write up a solution for each part of the problem.
- Keep a chart recording each of the different ways of solving each part of the problem. Add to it over time as ideas come to you and the class.
Extension
How many ways can you show that (1), (2) and (4) are triangular numbers?
Solution
Note that in a question like this you have to do one of two things. If you believe an expression is wrong, then it is often easiest to show that it is wrong for one particular value of n. On the other hand, if you believe that it is right, then you have to justify this by showing that it is equal to an expression that you know is right.
- This is an expression for the nth triangular number so we have to prove that this is the case. We do this by constructing the nth triangular number in counters.
The number of counters in the bottom row of the nth triangular number is n. The number of counters in the row above that is n – 1. The number of counters in the row above that is n – 2. This continues until you get to the top row with 1 counter. So
T(n) = n + (n – 1) + (n – 2) + … + 2 + 1.
- This is an expression for the nth triangular number so we have to prove that this is the case. We use an algebraic approach for this one.
Recall that the nth triangular number is formed by adding the first n numbers.
To show that (1) holds we use the backward/forward method from Square and Triangular Numbers, Level 5. Suppose that the nth triangular number is T(n). Then
T(n) = 1 + 2 + 3 + 4 + . . . . + (n – 3) + (n – 2) + (n – 1) + n
T(n) = n + (n – 1) + (n - 2) + (n – 3) + . . . . + 4 + 3 + 2 + 1
Then adding the two lines together gives
2 T(n) = (n+1) + (n+1) + (n+1) + (n+1) + . . . . + (n+1) + (n+1) + (n+1) + (n+1)
But there are n terms here so the right hand side of this expression is n x (n + 1). So
2 T(n) = n x (n + 1)
And this gives
T(n) = ½n(n + 1).
- This is not an expression for the nth triangular number so we only have to find one value of n for which it is wrong.
Put n = 2. Then becomes 1 + 3 + 5 + … + (2n – 5) + (2n – 3) + (2n – 1) = 1 + 3 = 4. But the second triangular number is 1 + 2 = 3. So expression is not equal to T(n).
- This is an expression for some nth triangular numbers so we have to prove that this is the case. We use an algebraic approach for this one.
To do this, we need to know the result for the difference of two squares.
The difference of 2 squares result is a2 – b2 = (a – b)(a + b). Geometrically it can be deduced as follows. Subtract a square of size b from a square of size a.

The difference is two rectangles. From the diagram we can see that dimensions (a – b) by b and the other (a – b) by a.
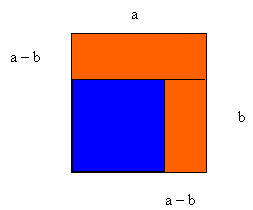
So the total area of the two rectangles is (a – b) x (a + b).
This show that a2 – b2 = (a – b)(a + b).
Now how are we going to use that on the expression for T(n)? Well, first note that the expression comes in pairs of squares one of which is subtracted form the other. For instance, the first pair is n2 – (n – 1)2. Since this is the difference between two squares we can apply a2 – b2 = (a – b)(a + b). In the first pair a = n and b = n – 1. So
n2 – (n – 1)2 = [n – (n – 1)][n + (n – 1)] = n + (n – 1).
Since this is two of the terms to be found as the last number in the sum that makes up T(n) in (1), that’s a good start.
Similarly, using the difference of two squares we can show that (n – 2)2 – (n – 3)2 = 2n – 5 = (n – 2) + (n – 3). And that’s another two terms.
Each difference pair down to 22 – 12 = 2 + 1, contributes a pair of terms in T(n). So it’s looking good for the expression of (4) to be equal to T(n). But just look a bit carefully. If we start from the low end and work up we get
(22 – 12) + (42 - 32) + (62 - 52) + (82 - 72) + …
= (1 + 2) + (3 + 4) + (5 + 6) + (7 + 8) + …
Here is the problem. We always get a pair of numbers from each bracket. So at the end of the day we don’t get
1 + 2 + 3 + 4 + . . . + (n – 3) + (n – 2) + (n – 1) + n
for every n. We only get it for n even. So the expression in (4) is only equal to T(n) if n is even.
- This is not an expression for the nth triangular number so we only have to find one value of n for which it is wrong.
Try n = 1. Then [(n + 1)2 + n2 + (n – 1)2 + ... + 12] – [(n2 + 2) + ((n – 1)2 + 2) +
((n – 2)2 + 2) + … + (12 + 2) + 2], becomes [22 + 12] – [3 + 2] = 0.
- This is an expression for the nth triangular numbers so we have to prove that this is the case. We use an algebraic approach for this one.
Note that this equation is called a recurrence relation or recurrence rule as it says how T(n) can be found recursively, step by step.
To see how this works we see that we are given T(1) = 1. Then we can get T(2) by substituting n = 2 in the first equation. So T(2) = T(1) + 2 = 3. Keep going to check out several more values of T(n).
Now that you are convinced that it works, start from the other end.
T(n) = T(n – 1) + n =[T(n – 2) + (n – 1)] + n = T(n – 2) + (n – 1) + n.
Successively repeating this process leads us finally to the expression for T(n) in (1). You should be able to see that this works for all values of n whether they are odd or even, so we don’t fall into the trap of (4).
This last recurrence rule form of T(n) is best proved by a form of mathematical proof called mathematical induction. This idea is too advanced for most students at this level but you may find an advanced student who can understand it.
Solution to the Extension
There are many other ways to show that these results hold or don’t hold.