The Topsy-Turvy Twins

Problem

Tina and Tom were twins. Tina saves and Tom spends. Tom found a $20 note on Sunday evening and spent $2 a day starting on Monday. Coincidentally, Tina started work that Monday and gets $2.50 a day. How long would it be before Tina has more money than Tom?

Teaching sequence

1. Pose the problem to the class. You may use 2 students to help establish the problem and interest the class in the problem.
2. Brainstorm for ways to solve the problem – list these on the board for the students to refer to as they solve the problem.
3. As the students work on the problem in pairs ask questions that focus on the strategy they have selected.
   What approach are you using? Why did you select that approach? Are you making progress?
4. Encourage the students to record their solutions in ways that clearly describe what they did.
5. Display and share written solutions.

Extension to the problem

Write you own twins problem for others to solve.

Solution

In the graph below, we sketch the situation. Diamonds represent Tom’s finances and squares represent Tina’s situation.

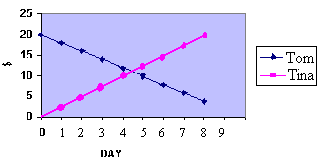
From the graph we can easily see that the small squares go above the crosses on day 5, Friday. So it is five days until Tina has more money than Tom.

Solution to the extension:

To do this algebraically we first have to find out the two rules for the number patterns produced by Tom and Tina’s activity. Now Tom started off with $20 and then spent $2 a day. So each day he had $2 less. His equation is

M = 20 – 2n

On the other hand Tina earns $2.50 each day and so her equation is

M = 2.5n

You should check these equations by putting in actual values for n.
If the two Ms can ever be equal we will have

2.5n = 20 – 2n, which becomes 4.5n = 20, so n is 4 and a bit.

If they are equal after 4 and a bit days, then one of them must have more for the first time on day 5. Since Tina’s money is increasing, she is just ahead on day 5.