In this unit students are asked to investigate mathematical relationships when they select various numbers to be used in a 3 circle configuration and in 6 circle configurations. They will explore both whole number and fractional numbers as they consider how various configurations impact on the relationships between numbers.
- Solve simple number problems.
- Solve simple problems involving fractions and decimals using any of the four arithmetic operations.
- Solve fraction problems using the basic operations where the fractions have a range of denominators.
- Use fractions, decimals, and negative numbers in novel situations.
The contexts of this unit are configurations of three circles but they are used as a basis for the practice of the four basic operations on whole numbers and fractions (or decimals) and for mathematical thinking. The numbers in the problems that you pose them need to be chosen suitably to force fractions or decimals to be required.
The unit is divided into five sessions: Mathematical Play; The Numbers and Sums Link; Numbers From Sums; Extending; and Reflecting. The sections are discussed individually below before the lesson sequence. Note that all of the sessions should include discussions in which the students say what they have discovered and, if possible, justify any claims they make. In the process you can observe which students are having trouble with fractions, decimals or negative numbers and may require more learning support.
Mathematical Play: In this section, which repeats the first session from Three Circles I, Level 3 the students start on the ideas of the problem. These are first putting whole numbers into the circles and considering the sums of the numbers on each side. This leads to looking at: can the side sums be equal; can two be the same; can they all be different; and if they are different what more can be said? They are being used to hone in on what might be interesting mathematical aspects of the problem and what might lead to interesting conjectures and even proofs (justifications).
The Heart of the Problem: There are two aspects of this problem. These are (a) going from numbers in the circles to the sums of the sides and (b) deducing the original numbers from the side sums.
The Numbers and Sums Link: In (a) one thing that is important is that the differences between the original numbers are the same as the differences between the side sums. This is easily shown by using a little algebra but it can be seen and extracted from numerous examples.
Show how to justify this with algebra. Let the circle numbers be a, a + r and a + s, with a < a + r < a + s. Then the side sums are 2a + r, 2a + s and 2a + r + s, with 2a + r < 2a + s < 2a + r + s. Notice that the differences in both the original numbers and the side sums are r, s and s – r but that for the circle entries, the difference between the smallest numbers is r, while for the side sums, the difference of r is between the largest pair.
In this exploration you might want to see what happens if (i) all of the numbers are equal; (ii) only two are equal; or (iii) three numbers are different. In (i) they should discover that if all of the numbers are equal then all the sums are equal. Note though that if only whole numbers are being used only even sums can be found. For (ii), only two of the numbers are equal. If only whole numbers are used, then one of these sums has to be even. In (i) and (ii), where even numbers are forced by whole numbers we can get odd numbers if we use fractions or decimals.
You might also lead the class to consider if, when the circle entries are fractions, can you get only one, precisely two, or all three sums to be fractions. Similarly, if the entries are allowed to include negative numbers, how many entries have to be negative in order to get no, one, two or three negative sums? (In the no case, you can have at most one negative number; for one, you can have one or two; for two you can have one or two; for three, two or three.) The students should be encouraged to look for examples to back up these claims.
Numbers From Sums: For aspect (b), there are at least three ways of finding the circle numbers from the side sums. Guess and check will always work but it is the least efficient. A second way is to use algebra, though this strictly involves solving linear equations in two unknowns which is beyond the algebra of Level 4. But the third way is foolproof and might reasonably be expected to be discovered by a Level 4 student. (There are minor variations of this method that might also be discovered.) The foolproof ‘guess and improve’ method is demonstrated using the example in the diagram below.
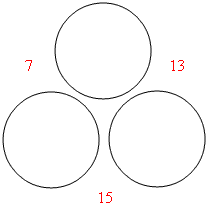
Since the smaller sums are 7 and 13, let’s assume that the original numbers were a = 0, a + r = 7 and a + s = 13. We show this guess in the diagram below.
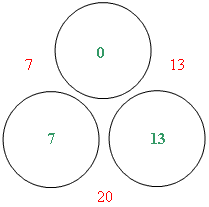
This is fine but it incorrectly has a bottom sum of 20 which is 5 more than we require. But we can fix that if we reduce both the 7 and 13 entries to 7 – 2.5 = 4.5 and 13 – 2.5 = 10.5. So here is where we are now.
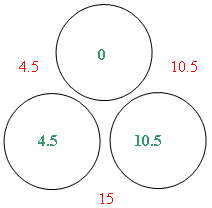
But we’re still not quite there. In the process of taking 2.5 off of each of the 7 and the 13, we have reduced both of the once-correct side sums to 4.5 and 10.5. However, if we add 2.5 to the top circle everything comes out right.
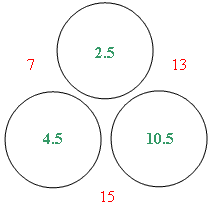
Students should be able to see that this three step method always works. Can they explain how this works?
Note that in this session you can try to show how you might ‘creep up’ on this result. Get some feeling for what happens by trying equal sums first and then just two equal sums, and so on. Can you get three equal sums with (i) whole numbers, (ii) fractions; (ii) decimals; or (iv) negative numbers? Can you get all possible sums that are same, same, different using each of the previous four types of number?
In order to encourage the application of operations on fractions, you might choose side sums that are themselves fractions. If the sum of the smaller two sums is less than the third sum, they will need to use negative numbers too.
An Extension: Recall that an extension is a problem that has features of the original problem. However, solving the extension does not lead to a solution of the original problem. In this way it differs from a generalisation.
The extension that we have suggested for this session is to replace addition by multiplication. We give an example below.
All of the same questions that were asked for the original problem can be asked again here. Once again, perhaps the most interesting question is how can we get the original circle entries given the side products?
This question gives rise to some interesting factorisation practice that might lead to some insight into how to efficiently go back.
A similar foolproof method can be used to go back from given side sums to circle entries when we use products as when we used sums. Instead of starting with 0 though you should to start with 1. The most general of the cases uses square roots though so you might want to avoid this by only giving them special products. In the session outline we provide a few examples of the type that will work without surds (that is, a quantity that cannot be expressed in rational numbers).
Reflecting: In this session students might like to experiment with their own generalisations and extensions. They might work on the Six Circles problem of Three Circles I, Level 3, or four circles arranged in a square, or five circles arranged in a pentagon, or … or addition replaced by subtraction or division. The questions of the earlier part of this unit should be used as a guide to finding interesting questions here.
New problems should be considered too. For example, if four circles are arranged in a square four equal sums that are either even or odd can be produced without the use of fractions. This is not the case if five circles are used. Do even and odd circle configurations work differently somehow?
Getting Started: Mathematical Play
- With the students all together give them the following instructions:
I want you to each take one of the Three Circle sheets (show them one) and put any numbers you like into the circles. For instance, give me three numbers. (Take some numbers from the students, say, 5, 7 and 11.) The numbers can be as big or as small as you like but you can only put one number in each circle.
Then I want you to add up the two numbers on each side of each of the Three Circle figures. (Let them find the side sums from their example. The one above gives 12, 16 and 18.) When you’ve done a whole sheet we’ll come back and discuss what things you have found. You might want to put your experiments, your mathematical play, together in a list. - Give each student a Three Circle sheet and let them work on 8 examples. Encourage them to record their various numbers and consequent side sums. As they are working check to see that everyone understands the task correctly. When the students have each produced 8 examples, bring the class together again. Find out what side sums they managed to get.
- Did anyone get three equal side sums on one of their Three Circles? (Discuss what they found.)
Did anyone get two equal side sums and a third different one on one of their Three Circles? (Discuss what they found.) Are there any other possibilities for the three side sums? They should realise that the three side sums could all be different. Were any of these side sums consecutive like 3, 4, 5? (Discuss what ‘consecutive’ means and what they found.)
In the discussions above, make sure that all the answers they have obtained are correct and list them on the board under each category. If only a few of any one case have been found, then the students will need to go back to work to find some more examples. - Once you have a reasonable number of examples of each type see if the class as a whole can make any conjectures about them. Here are some possibilities. When you get three equal side sums (i) you had to use the same number in each circle; (ii) the side sums had to be even. When you get consecutive side sums you only get one even number as a side sum. Whatever differences there are between circle entries are mirrored in the side sums.
- Write these conjectures on a sheet of paper and put them on the board for the rest of the week. Keep adding to this list. Place a tick against any conjecture that you can justify.
Exploring
In the next three teaching sessions, the students will investigate the links between the circle entries and the side sums. They will then consider an extension of the Three Circles, where products are used instead of sums. Similar questions to the ones we have asked so far can now be considered.
1. The Numbers and Sums Link
In this session take all of the Conjectures that you have made that go from circle entries to side sums and try to justify that they work no matter what the circle entries are. We suggest an approach here.
- Using whole numbers in the circles, what happens if all of the numbers are equal?
Experiment, make a conjecture, and see if you can justify it. - Do you get anything different happening if the numbers you use in the circles are fractions, decimals or negative numbers?
Experiment, make a conjecture, and see if you can justify it. - Repeat 1 and 2 if two of the circle entries are the same.
- Repeat 1 and 2 if the three circle entries are all different.
- Use class discussions to check the various conclusions.
2. Numbers From Sums
In this session work the other way. That is, start from side sums and discover how to go back to circle entries. We suggest that you first get them to see how to work back from equal side sums to the original circle numbers. Then consider what happens if the side sums are consecutive or all differ by some constant. How do you get the circle entries in this case? Finally, experiment with arbitrary side sums.
We give some sums that might initiate discussion. Try to find the circle entries in each case and then try to make general statements about the particular cases.
- What are the circle entries if the sums are: (i) 10, 10, 10; (ii) even, same even, same even again?
- What are the circle entries if the sums are: (i) 11, 11, 11; (ii) odd, same odd, same odd again?
- What are the circle entries if the sums are: (i) 10, 10, 12; (ii) even, same even, different even?
- What are the circle entries if the sums are: (i) 10, 10, 11; (ii) even, same even, odd?
- What are the circle entries if the sums are: (i) 7, 7, 10; (ii) odd, same odd, even?
- What are the circle entries if the sums are: (i) 7, 7, 13; (ii) odd, same odd, different odd?
- What are the circle entries if the sums are: (i) 10, 10, 7; (ii) even, same even, odd?
- What other variations are there on 3., 5. and 6.?
- Can you find a way of finding circle entries that will work for any three given sums?
3. Extending
In this session ask your class what extensions and generalisations are and talk about the extension where addition is replaced by multiplication. Recall all of the questions (and answers) that have been made during the previous sessions and see which of these questions can be used again here. What new questions come up because of the change in operation?
Encourage the class to answer and justify as many of the questions that they pose as possible. Remind them that some of the ideas they had in the earlier work might still work here.
- First explore from circle entries to products.
- To help the students, share this list of products with which they might want to experiment. What circle entries give these products? Can these products be obtained using more than one set of circle entries?
(i) 9, 9, 9; (ii) 6, 14, 21; (iii) 6, 10, 15; (iv) 15, 21, 35; (v) 12, 33, 44. - What about these products? How can you get them?
(i) 6, 8, 12; (ii) 6, 12, 18; (iii) 6, 18, 27; (iv) 42, 72, 84; (v) 132, 198, 216. - Can you find a general method to go from the three products to the three circle entries? Check that it works on all of the examples above.
- Does it work on these products?
(i) 72, 120, 240; (ii) 216, 432, 648; (iii) 25 x 34; 26 x 35; 27 x 35.
Reflecting
Students should be allowed to branch out in whatever direction they find interesting. Again discuss what generalisations and extensions are and then let them discuss what possible generalisations and extensions can be made to the Three Circles problem. Earlier we suggested the Six Circles problem, four circles arranged in a square or five in a pentagon or … or using subtraction or division. Let them follow up one or two of these. Then have a class discussion to see what results they have been able to find.
Dear family and whānau,
This week your child can tell you what we have been doing with numbers in circles. This has been a way of both refreshing number facts around the four operations of addition, subtraction, multiplication and division. It has also been a way of thinking mathematically about the relationships between numbers. Below we have six circles in a triangle.
Ask your child to explain how the side-sums are found and what observations they have made so far. Can they show you how to create configurations that have three side sums that:
- are all the same?
- the sides all equal 9?
- use the numbers 1-6?