The purpose of this unit is to engage students in applying their understanding of geometric thinking to design and describe formations and the translations and/or rotations needed to create those formations. This is explored in the context of choreographing a synchronised swimming routine and related patterns.
- Find the size of angles.
- Describe the features of regular polygons, including the size of their interior angles.
- Apply knowledge of angles, quadrilaterals, and regular polygons to problem solving contexts.
In this unit, students apply their understanding of geometry to design and describe shapes, formations, and the transformations that map one formation onto another.
To ensure engagement and participation in this unit, you should consider your students' prior knowledge of angles, polygons, quadrilaterals and problem solving tasks involving these ideas.
This cross-curricular, context-based unit aims to deliver mathematics learning, whilst encouraging differentiated, student-centred learning.
The learning opportunities in this unit can be further differentiated by providing or removing support to students, and by varying the task requirements. Ways to differentiate include:
- providing materials (e.g. shape tiles, protractors) to support students' thinking
- roaming and supporting students in a variety of groupings to ensure they understand the task at hand, the skills needed to succeed, and can apply these skills in a suitable process
- varying the amount of structured scaffolding and guided teaching you provide to students when investigating new tasks
- providing opportunities for students to create their own problems
- providing extended opportunities for students to revise and apply learning from throughout the unit
- modelling the application of ideas at every stage of the unit
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities (e.g. measuring angles).
With student interest engaged, mathematical challenges often seem more approachable than when presented in isolation. Therefore, you might find it appropriate to adapt the context presented in this unit. For example, problems could be acted out by students on land as dance formations or used to make connections with a wider focus on on swimming and water safety. Students might also be engaged by the task of creating and interrogating formations of people in other sports teams and groups.
Structure
The first session is an introductory activity that is aimed to spark the imagination of students, to introduce the need for a particular idea or technique in mathematics that would enable them to explore deeper into that context. It is expected that rich discussion may be had around the context and around the nature of the mathematics involved.
Following the introductory session, each subsequent session in the unit is composed of four sections: Introducing Ideas, Building Ideas, Reinforcing Ideas, and Extending Ideas.
Introducing Ideas: It is recommended that you allow approximately 10 minutes for students to work on these problems, either as a whole class, in groups, pairs, or as individuals. Following this, gather the students together to review the problem and to discuss ideas, issues and mathematical techniques that they noticed during the process. It may be helpful to summarise key outcomes of the discussion at this point.
Building Ideas, Reinforcing Ideas, and Extending Ideas: Exploration of these stages can be differentiated on the basis of individual learning needs, as demonstrated in the previous stage of each session. Some students may have managed the focus activity easily and be ready to attempt the reinforcing ideas or even the extending ideas activity straight away. These could be attempted individually or in groups or pairs, depending on students’ readiness for the activity concerned. The students remaining with the teacher could begin to work through the building ideas activity together, peeling off to complete this activity and/or to attempt the reinforcing ideas activity when they feel they have ‘got it’.
It is expected that once all the students have peeled off into independent or group work of the appropriate selection of building, reinforcing and extending activities, the teacher is freed up to check back with the ‘early peelers’ and to circulate as needed.
Importantly, students should have multiple opportunities to, throughout and at the conclusion of each session, compare, check, and discuss their ideas with peers and the teacher, and to reflect upon their ideas and developed understandings. These reflections can be demonstrated using a variety of means (e.g. written, digital note, survey, sticky notes, diagrams, marked work, videoed demonstration) and can be used to inform your planning for subsequent sessions.
The relevance of this learning can also be enhanced with the inclusion of key vocabulary from your students' home languages. For example, te reo Māori kupu such as koki (angle), taparau (polygon), koki roto (interior angle), and tapawhā (quadrilateral) might be introduced in this unit and then used throughout other mathematical learning.
- Images of synchronised swimming formations used throughout the unit
Session One
This session introduces the context of synchronised swimming in an angle problem. You could adapt the context of this unit to reflect a different sports or dance team, or other group. It might also be valuable to investigate the given synchronised swimming context, before asking students to create their own problems (perhaps as an extension or paired task) relevant to a different context (e.g. kapahaka formations).
Introduce the following context to students: Five synchronised swimmers spread their arms out straight (at an angle of 180° apart). They join hands making an obtuse angle between each adjacent pair of swimmers arms. There are no gaps in the formation and the swimmers arms have formed a regular polygon.
Support students to find the size of the obtuse angles made by the swimmers joining hands.
As your students work, observe their approach to solving an angle problem. Students may use reasoning, or practical techniques to work towards a solution. Use these observation to locate your students on the geometric thinking learning progression.
Discuss, drawing attention to the following points:
- What is the name of the regular polygon formed by their arms?
- Will the swimmers be able to make this polygon facing inwards or outwards?
- If their arms are not held straight out (i.e., their arms don’t make an angle of 180°), what other regular polygon can these five swimmers make with their arms? What would the size of the interior angles need to be for this to be a regular polygon?
Session Two
Introducing Ideas
- Present students with the following image. Ask them to look at the shape made by the arms of the 8 synchronised swimmers:
Discuss, drawing attention to the following points:
- How many sides does this shape have?
- Name the shape.
- Describe the symmetry of this shape.
- Find the size of the interior angles of this shape.
- Is this shape a regular polygon?
- What approximations did you make to decide on the number of sides and the regularity of this shape?
- What are the physical requirements of the 8 swimmers to be able to form this figure?
Building Ideas
- Present students with the same image of 8 synchronised swimmers. Provide time for students to discuss the following points:
- Name the shape made by the legs of the 8 swimmers.
- Is this a regular polygon?
- Find the lines of symmetry of this polygon.
- What is the rotational symmetry of this polygon?
- What is the order of symmetry of this polygon.
Reinforcing Ideas
- Present students with the same image of 8 synchronised swimmers.
- Explain: The acute interior angles of the shape, made by the legs of the 8 swimmers, are each 45°. What is size of the interior reflex angles?
Extending Ideas
- How would the shape made by the arms vary if there were only 6 swimmers?
- What would the internal angle of the shape made by the arms be with only 6 swimmers?
- Could only six swimmers make a star formation with their legs extended, like that made by the 8 swimmers? Give you answer in terms of angles and lengths of sides.
Session Three
- Present students with the following image. Ask them to look at the shape made by the right legs of the 8 synchronised swimmers:

Discuss, drawing attention to the following points:
- How many sides does this shape have?
- Name the shape.
- Describe the symmetry of this shape.
- Find the size of the interior angles of this shape.
- Is this shape a regular polygon?
- What approximations did you make to decide on the number of sides and the regularity of this shape?
- What are the physical requirements of the 8 swimmers to be able to form this figure?
Building Ideas
- Present students with the same image of 8 synchronised swimmers. Draw attention to the 8 divisions within this formation of the 8 synchronised swimmers. Provide time for students to discuss the following points:
- Name the shape made by the legs of the 8 swimmers.
- Is this a regular polygon?
- Find the lines of symmetry of this polygon.
- What is the rotational symmetry of this polygon?
- What is the order of symmetry of this polygon?
Reinforcing Ideas
- Present students with the same image of 8 synchronised swimmers. The shape is (approximately) an octagon divided into 8 kites. The angle made by the bent knees of the right legs of the 8 swimmers are each 75°.
- Have students consider: What is size of the interior angles of the kite shapes within this formation?
Extending Ideas
- Present students with the same image of 8 synchronised swimmers. Draw attention to the divisions within the (approximation of an) octagon formation made by the right legs of the 8 synchronised swimmers.
- Provide time for students to discuss the following points:
- How would the shape of the formation and the divisions vary if there were only 6 swimmers?
- What could the internal angle of the divisions made by the left legs be with only 6 swimmers? State any assumptions you have made.
- Describe the symmetry of the divisions and the overall shape of the formation that would be made by only 6 swimmers in this position.
Session Four
Introducing Ideas
- Present students with the image of red swimmers. Ask them to look at the flower figure of red swimmers below, made by swimmers holding adjacent swimmers’ feet.

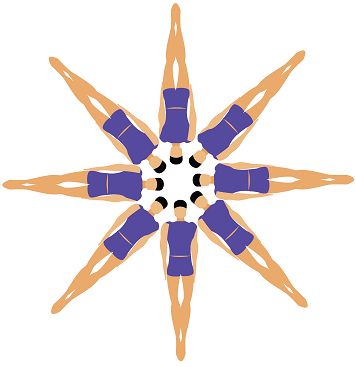
- Present students with the image of purple swimmers. Provide time for students to discuss the following points:
- How many swimmers are needed for this formation?
- How many petals are there in this flower formation?
- What is the angle between each of the petals in this flower? Explain how you found this angle.
- Could a pattern be formed using swimmers in the same position for a 5 or a 7 petal flower? What changes would need to be made?
- How could the rotational symmetry of the formation be used for effect in a synchronised swimming performance?
Building Ideas
Provide time for students to discuss the following points, in relation to the formations of red and purple swimmers:
- Snowflakes have rotational symmetry of order 6. Which figure(s) could be used in a sequence about snowflakes?
- What is the order of rotational symmetry of the other figure?
Reinforcing Ideas
- Provide time for students to discuss the following points, in relation to the formation of purple swimmers:
- What is the order of rotational symmetry of this figure?
- Find the angle between adjacent swimmers.
- How many mirror lines are there in this formation?
- What is the total order of symmetry of this formation?
- Describe the formation that would result if only 6 swimmers were used in the same position and evenly spaced around a focal point. Give angles and a description of the symmetry of this new formation.
Extending Ideas
- Provide time for students to discuss the following points, in relation to the formations of red and purple swimmers:
- How many swimmers are needed for each formation?
- What is the angle between (the central axes of symmetry of) adjacent swimmers in each formation?
- Can you generalise the relationship between the number of swimmers (n) and the angle between the adjacent swimmers (A) when they're evenly spaced in formations?
Session Five
Introducing Ideas
Present students with the following image. Ask them to describe the symmetry of the formation made by the 8 swimmers:

Discuss, drawing attention to the following points:
- What polygons can you see in this formation?
- Could a pattern be formed using an odd number of swimmers in the same position?
- How could the rotational symmetry of the formation be used for effect in a synchronised swimming performance?
Building ideas
- The arms and legs of each swimmer form four sides of a chevron. Provide time for students to do the following:
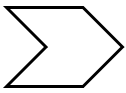
- Locate these chevrons.
- If the angle between the swimmers’ legs are all 60°, find the size of each of the interior angles of each chevron.
Reinforcing ideas
- Provide time for students to do the following:
- Locate these chevrons.
- Use the symmetry of the shape to find possible sizes of the interior angles of the chevrons.
- Explain your working using geometric reasoning.
Extending ideas
- Present students with an image of the initial formation. Provide time for students to complete the following tasks:
- Give instructions (using angles and leg lengths) that would allow these synchronised swimmers to transition from this formation to one that:
- Has all swimmers evenly spaced around a focal point
- Has their arms extended and touching
- Has their legs in the same position (30° apart).
- Describe what would happen if, once in the new formation, the swimmers holding hands pull their arms in by their sides. Include any limiting factors in your description.
Session Six
Introduce the following context to students: Synchronised swimmers spread their arms out straight making an angle of 180°. They join hands making an angle of 144° between each pair of swimmers arms. There are no gaps in the formation and the swimmers arms have formed a regular polygon.
Name that polygon.
Discuss, drawing attention to the following points:
- What do you know about the interior angles of regular polygons that would help you to solve the problem?
- Could you find a practical way of solving this problem?
- How many swimmers are needed for this formation?
Building Ideas
Provide time for students to work through the following tasks:
Design a formation that uses 6 synchronised swimmers and creates a closed regular shape that has rotational symmetry of order 6, has 6 mirror lines, and tessellates.
Find the sizes of the internal angles of the divisions within this formation.
Reinforcing Ideas
Provide time for students to work through the following tasks:
Design a formation that uses 8 synchronised swimmers and creates a closed regular shape that has rotational symmetry of order 4, has 4 mirror lines, and tessellates.
Find the sizes of the internal angles of the divisions within this formation. Give geometric reasons where possible.
Extending Ideas
Provide time for students to work through the following tasks:
Design a formation that uses 6 synchronised swimmers and creates a closed regular shape that has rotational symmetry of order 3, has 3 mirror lines, and tessellates.
Give instructions, using angles and leg lengths, that would allow your 6 synchronised swimmers could transition from this formation to one that has rotational symmetry of order 6, has 6 mirror lines, and tessellates.
Dear parents and whānau,
In class, we have been exploring the features of regular polygons, including the size of their interior angles, in the context of synchronised swimming formations. Ask your child to share their learning with you.
