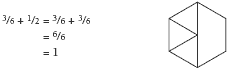This is a level 3 number activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (244 KB)
write a fraction label for a diagram
write a fraction story
For this activity, the students need to be able to read and write fractions and understand that fractions are part of a whole and part of a set.
Before the students begin this activity, they should have had experience with finding fractions of a stack of objects, such as multilink cubes. If they have not, you could introduce fractions to them in the following way.
The students need to understand that a fraction is a part of all the units in the stack. If you take a stack of 6 cubes, made up of 5 red cubes and 1 white cube, 5/6 of the stack is red and 1/6 of the stack is white. You could then change the number of colours but keep 6 cubes in the stack. “If I have 3 blue cubes and they make up 3/6 of the stack, how much of the stack is left?” Now change the number of cubes in the stack so that the students are introduced to the idea that they have to know what the “whole” is before they can work out the proportion of the parts of the whole.
You will need to encourage the students to make connections between the fractions written in words and those written numerically. Often the students can tell you about parts of a whole but cannot match the concept with the written words or numerical symbols.
This activity introduces the students to stacks made up of 3 or more colours, and they have to find what fraction each colour is of the whole. Encourage the students to model the flying discs with stackable cubes before they answer the questions. The example shows a stack of 11 discs made up of 3 colours. It then introduces the addition of the three parts: 5/11 + 4/11 + 2/11 = 11/11 or 1 whole.
The students need to be aware that in a fraction sentence, the numerators (in this case, 5 + 4 + 2) add up to the common denominator (11). This can be easily modelled and provides the basis for a good understanding of what is required in question 2.
In question 1, the students need to realise that each stack is a complete set, and therefore the fractions deal with each stack individually and cannot be directly compared with the fractions for the stack before or after.
Question 2 asks the students to write addition equations for each of the stacks in question 1. Have the students refer back to the fraction stories they wrote in words in question 1c.
Further discussion and investigation
The students may need further practice with this concept of fractions before they fully understand it. Use sets of marbles, counters, or farm animals (from the Beginning School Mathematics materials) and encourage the students to find and write fraction sentences for various sets.
The students could also investigate what fractions of the class are male, have long hair, have fruit in their lunch, and so on to explore this concept.
Use pattern blocks (sets of geometry shapes, including hexagons, triangles, trapezia, and rhombuses) to explore other fraction addition problems. For example, 3 triangles plus 1 trapezium is the same as 1 hexagon.
The students could also revisit Stacking Up and find and write fraction subtraction stories.
Answers to Activity
1. a. i. 3/8. (3 eighths)
ii. 1/3. (1 third)
iii. 5/8. (5 eighths)
iv. 3/5. (3 fifths)
v. 2/7. (2 sevenths)
vi. 1/12. (1 twelfth)
b. i. 1/8. (1 eighth)
ii. 2/3. (2 thirds)
iii. 2/8 (2 eighths) or 1/4 (1 quarter)
iv. 2/5. (2 fifths)
v. 4/7. (4 sevenths)
vi. 8/12 (8 twelfths) or 3/4 (3 quarters)
c. i. Yellow + Blue + Pink + Green
3 eighths + 1 eighth + 3 eighths + 1 eighth = 8 eighths = 1 whole
ii. Yellow + Blue
1 third + 2 thirds = 3 thirds = 1 whole
iii. Yellow + Blue + Green
5 eighths + 2 eighths + 1 eighth = 8 eighths = 1 whole
iv. Yellow + Blue
3 fifths + 2 fifths = 5 fifths = 1 whole
v. Yellow + Blue + Green
2 sevenths + 4 sevenths + 1 seventh = 7 sevenths = 1 whole
vi. Yellow + Blue + Pink + Green
1 twelfth + 8 twelfths + 1 twelfth + 2 twelfths = 12 twelfths = 1 whole
2. i. 3/8 + 1/8 + 3/8 + 1/8 = 8/8 = 1
ii. 1/3 + 2/3 = 3/3 = 1
iii. 5/8 + 2/8 + 1/8 = 8/8 = 1
iv. 3/5 + 2/5 = 5/5 = 1
v. 2/7 + 4/7 + 1/7 = 7/7 = 1
vi. 1/12 + 8/12 + 1/12 + 2/12 = 12/12 = 1