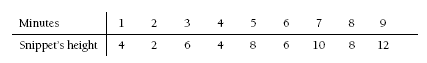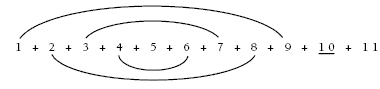Slippery Solutions

Problem One

Making a vertical number line and using a peg to track Snippet the Snake’s position at each minute is a useful model. Organising this data in a table can also be helpful:

So Snippet reaches the top of the pole in 9 minutes. (If the pattern were to continue, he would slip back 2 metres after that ninth minute, unless he hangs on tight!) Some students will give an answer of 12 minutes based on the pattern that on every even number of minutes, Snippet is that number of metres up the pole.
Encourage the students to generalise the process by varying the conditions of the problem. For example:
“What if the pole were 20 metres high?”
“What if Snippet went up 5 metres each time and then slid back 2 metres?”
In general, for any height of pole, Snippet can climb the “up” distance on the last minute. So students need to count 1 minute for this and take the up distance off the height. Since his net gain for every two minutes is the difference between the up distance and the down distance, find out how many times this net gain will go into the remaining height. For example:
“Snippet climbs up 5 metres in the first minute and then slips back 2 metres in the second minute, and so on. The pole is 17 metres high. How long will Snippet take to reach the top?”
17 – 5 = 12 gives the metres to be climbed by net gains.
5 – 2 = 3 gives the net gain.
12 ÷ 3 = 4 gives the number of 2 minutes needed to reach 12 metres.
So Snippet takes 1 + (4 x 2) = 9 minutes to reach the top.

Problem Two

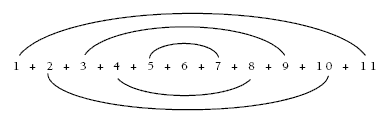
Students will need to find the sum of the first 11 counting numbers, 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11. Encourage them to look for patterns to make the calculation easier. For example:
Look for numbers that add to 10:

… so the answer is (5 x 10) + 5 + 11 = 66
Look for pairs of numbers with the same sum, in this case, 12:

… so the answer is (5 x 12) + 6 = 66
You may want to tell the students the story about a famous mathematician called Gauss, who found the sum of the numbers 1 + 2 + 3 + … + 98 + 99 + 100 with remarkable speed at the age of nine. He used the method above and astounded his teacher.

Problem Three

Students will need to understand the dynamics of balancing scales to solve the problem. If necessary, relate this to a see-saw. A logical line of reasoning would be:
i. Three lots of B have a mass of 24, so one lot of B must have a mass of 8.
ii. Two lots of B have the same mass as A, and because B has a mass of 8, A must have a mass of 2 x 8 = 16.
These types of problems help develop algebraic thinking, particularly the ability to handle unknowns. Try varying the conditions of this problem, for example:
“What if four lots of B had a mass of 24?”
“What if two lots of A and two lots of B had a mass of 24?”

Problem Four

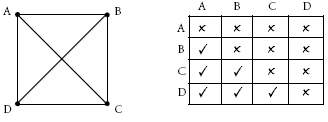
This problem is easily modelled by acting it out with the students.
Alternatively, students can represent the problem using a diagram or table:

Encourage students to generalise their methods by extending the pattern to include five people shaking hands

Answers to Problems

1. 9 minutes
2. 66
3. 16
4. 6