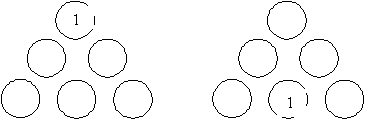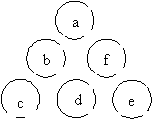This problem solving unit is suitable for Level 5 (or Level 6) students.
In this problem solving unit, we look at numbers that fit into a triangular arrangement of circles. The point of this unit is to give students a chance to
- see how mathematicians operate
- display ingenuity and creativity
- practice arithmetic in context
- learn what generalisations, extensions, conjectures, theorems, and proofs are
- work through a completely novel situation and try to develop a mathematical theory around it
- Solve a mathematical problem.
- See how to generalise and extend a problem.
- Understand why and how mathematical statements may be justified.
- Work with others to solve a problem and generate ideas.
Like all of the Problem Solving units, this one aims to introduce students to the underlying ideas of mathematics through a problem. The problem here requires only a simple knowledge of arithmetic but the process we go through demands a considerable use of ingenuity and creativity. In this unit we see how a mathematical theory might develop through experimentation, conjecturing, proving, generalising and extending. We also see that some proofs are ‘nicer’ than others.
As with all of these units it is difficult to break the development here up into lessons as we can never be quite sure how any particular class will progress. This will depend both on their ability and on your scaffolding. The right question asked at the right time will enable more rapid progress. However, you don’t want to make it too rapid!
Again like many of the units this one can be used at a variety of Levels. We have used it with students from 8 years old upwards. (It also makes a useful workshop for teachers.) Naturally you will expect older students to get further. With younger students it is probably enough to get all four answers and to make conjectures about the sorts of sets that will work and the number of answers that might be possible. But most classes we have worked with can be scaffolded into noticing Method 4 of the proof that there are only four answers for 1, 2, 3, 4, 5, 6. They can also start on the Eighth Circle Problem and the Homelink.
If your class hasn’t attempted the V-sets Problem Solving unit, we suggest you do that before this unit as it will give your students a good lead into some of the ideas that we used here.
As we have listed this unit for Levels 5 and 6, we have included some algebra. This may be omitted if you feel that it is too hard for your class. However, it might be a good extension aspect of the main problem and be valuable for your brighter students.
- Pencils
- Paper
Lesson Sequence
Session 1
Discover all four answers to the Six Circle Problem and be reasonably convinced that there are no others. Attempt to show that this is the case. What can you say abut the answers you have found?
Background
First we start off with the problem on which this whole unit is based.
Basic Problem (The Six Circle Problem): Is it possible to put the numbers 1, 2, 3, 4, 5, 6 in the circles so that the sums of the three numbers on either side of the triangle are the same?
Before you take the problem to the class it’s worth giving it a bit of thought. There are a few things that need to be considered.
- Don’t worry too much about getting students to find a formula or method to do this problem. The important thing for them to do at the start is to use their intuition. What that really means is to encourage them to try anything that comes into their minds. So encourage them to guess, to play around, and don’t worry about what method they use even if it seems totally unmathematical!
- Then, when they start to get answers, you will need to get them to think about which answers differ from each other. The point is that once they get one answer they can get another five simply by using the rotations of the equilateral triangle. Because we can get any one of six from the others here, we might as well say that they are all the same. So we’ll say that the two answers below are the same.
- So what answers exist and how many of them are there? Trial and error will produce four at least. We show them below. But are there any more that we haven’t shown yet?
- It’s important to note the sums of the sides for two reasons. First, we need to check that the sum on all three sides is the same to be sure that we have a proper answer. Second, the sum will prove to be fundamental in what follows.
Now what can we say about the answers? Is there any relation between them? Are there any patterns that we ought to see? Here’s a list of some of the things that your students might find.
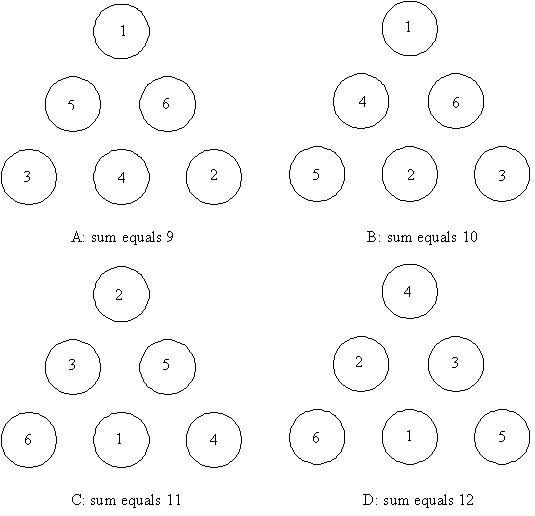
- The corner circles contain 1, 2, 3; 4, 5, 6; 1, 3, 5; and 2, 4, 6. These are the smallest and largest consecutive numbers, the odd numbers and the even numbers.
- If you move the numbers on one answer all round one circle, you get another answer. It doesn’t matter which way you move them: clockwise or anti-clockwise. Using this move, A becomes D becomes A and B becomes C becomes B.
- Changing corner numbers to the middle and vice-versa changes one answer into another. This causes the same switches as the last item on the list.
- The difference between opposite corner and middle numbers is the same. Look at A. 4 is opposite 1 and 4 – 1 = 3. 5 is opposite 2 and 5 – 2 = 3. 6 is opposite 3 and 6 – 3 = 3.
- If you replace every number m by 7 – m, you get another answer. So in B if you replace 1 by 6, 2 by 5, and so on, B turns into C.
We don’t claim that this is an inclusive list. If your students find some other properties of the four answers we’d be glad to hear about them and add them to the list.
Teaching Sequence
- Treat this like any of the Problem lessons that can be found elsewhere on this site. Introduce the problem and discuss it to ensure that all of the students understand what the question is asking and how it might be tackled. Then, in groups of 2 to 4, give students the chance to solve the problem.
- As groups come up with answers, encourage them to find more answers by asking ‘Can you find any more?’. Do this even when they have obtained all four answers. Also encourage them to think about when two answers are the same or different. (‘Is that answer the same as any of the others you’ve found?’ ‘Can you get that answer from that one?’) Give everyone a chance to make some progress on the problem. This may mean that you will need to suggest some corner numbers or if they have some numbers in correct positions, you may need to tell them that those are OK but they might think about moving others somewhere else.
- When they think that they have found all of the possible answers, encourage them to prove that the answers that they have found are the only ones that exist. (‘Why do you think there are no more answers?’) As part of this process get them to think how the answers are related to one another as we have done in the list of five points above. This list will be useful later and is a good mathematical tool – look at what you’ve got to see if there is some way that you can understand it more.
- Have a class discussion on the results of the exploration so far. Get different students to write up one answer on the board until they see when two answers are the same (because of the symmetry of the triangle) and that there seem to be only four answers. Produce a conjecture on the number of answers.
- Finally have a think-tank session to generate ideas for the next lesson. How might we prove/justify that there are just four answers? What are the key ideas? How might we restrict the problem?
Note that you may well think of ideas that we have not covered here. It is important that you follow them through to see where they lead. If you get some nice results please let us know so that we can tell others. We’ll certainly acknowledge anything of yours that we put on the web.
Session 2
Show that there are only four answers to the Six Circle problem.
Background
So how and why are there only 4 answers to the original question? And how can we go about establishing this beyond all reasonable doubt? There are actually several ways to do this. We will list them here for use in the next two sessions. Part of the reason for doing this is to show that there are many ways to prove or justify things. In some way each of them is equally valid. However, there are some proofs that are ‘nicer’ or ‘more efficient’ or ‘more sophisticated’ than others are. We will provide some proofs below and comment on their quality.
- “I have worked at this for 15 minutes now and can’t find any more. So there must be only four.”
This isn’t a proof. We can’t be sure that we couldn’t find another answer given some more time on the problem. Or maybe someone smarter than us could find another answer. Or maybe someone in another country could. There’s too much room for doubt here. This is not the basis for a mathematical proof.
It may, however, be the best that we can do. For instance, at one stage we thought that there were just 7 planets. We had looked at the heavens for thousands of years and had seen only 7. But then along came John Adams and he said that if Newton’s equations of motion were correct, there was something funny going on up there. There was some ‘wobbling’ of the planets that suggested to him that there was another planet out there that we hadn’t come across by 1845. He calculated where the planet should be and then someone went looking and eventually found it in September 1846.
If we haven’t got the tools to settle something we may have to rely on the ‘I can’t find any more’ approach. While this may constitute the best state of our knowledge at some point, in mathematics it is at best a conjecture – a guess at what the answer actually is. Mathematics requires a proof, a justification that cannot be faulted. The problem is that if you work for another 10 minutes you might just find another answer.
- “I have worked out all of the possibilities and there are only four answers.”
This is a good enough proof provided it can be shown that all possible cases have been looked at. What would have to be done here is to list all possible ways of putting the numbers 1 to 6 into the 6 circles and then taking from this list the ones that give equal sums on all three sides.
One way to do this would be to write a computer program. On the face of it there are 6 ways to put in the first number, 5 to put in the next and so on. Hence there are 6 x 5 x 4 x 3 x 2 x 1 = 720 ways of putting in the 6 numbers. This wouldn’t take a computer very long. You could even get the class to do it in a reasonable time by dividing up the cases between them. We give a way of doing this below that means we don’t have to consider all of the 720 possibilities.
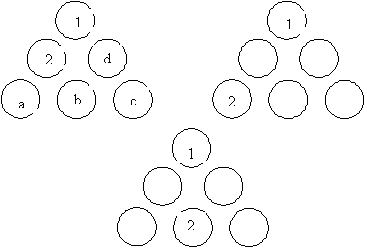
Think about where to put the number 1. Because of the symmetry of the triangular shape, there are only two places to put the 1: in a corner circle or in a circle in middle of a side. We show these two situations below.
At the next stage, we want to put a 2 in all possible places. This can be done in three ways for each of the ways of putting in a 1. Because it is tedious we will only do it for one case. If you want to you could get your class to complete the argument.
Now in the first of these three situations, we can put 3 in four places. The symmetry of the triangle doesn’t help us now at all. If we put 3 in the ‘a’ circle then the side we have produced has a sum of 6. There is no other way to make up 6 so there is no answer possible here.
If we put 3 in the ‘b’ circle, then we get a sum of a + 3 on the left side and a + 3 + c on the bottom side. They can never be equal.
If we put 3 in the ‘c’ circle, then a similar argument shows that the left side has a sum of a + 3 and the bottom has a sum of a + b + 3. These too can never be equal.
If we put a 3 in the ‘d’ circle we have to put 4, 5, 6 along the bottom in some order. This gives a sum that is bigger than can be made on the other two sides.
We leave you and your class to go through all the other cases. You could divide things up so that different groups of students did different cases. This would speed things up. Perhaps the only consolation of doing it this way is that this is a lot easier than doing 720 different cases. But it ain’t pretty. We would hope that there was a better way.
As much as anything, the above is an exercise in being systematic. It’s important do things carefully and in some order so that every possibility is covered.
- Parity – odds and evens. “Where can I put the even numbers and where can I put the odd numbers?”
The argument here is based on the fact that the sum of two even numbers is even; the sum of two odd number is even and the sum of an even and an odd number is odd.
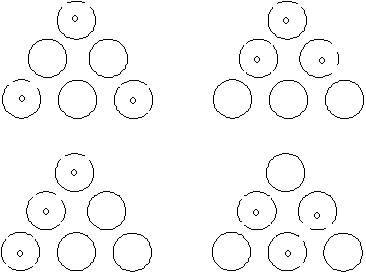
Now there are just three odd numbers and we can either have an odd number of odd numbers on one side of the triangle or we can have an even number. By careful consideration, we see that there are just four possible arrangements for the odds and evens. We show these below. The even numbers are in the blank circles and the odd ones in the circles marked with an ‘o’.
So we now know where the 1, 3, 5 go. Because of the symmetry of the equilateral triangle, there is only one way that the numbers 1, 3, 5 can be put into the first and fourth possibilities above. From there it is reasonably quick to see where the even numbers have to go. There are three possible arrangements of 1, 3, 5 in the other two cases. Working systematically will reveal the arrangements that work and those that don’t. When this has all been done we get the four answers we found earlier.
- Reduce the sums and produce the sums.
In this method of proof we first of all show that the sums that we can get on each side of the triangle in an answer, are fairly restricted. After all, can you have a side sum of 24, 18, 13, 12?
To do this think first about the 1. What is the biggest sum that 1 can be in? The biggest sum will be with 5 and 6 to give a sum of 12. So this is the largest sum we can get. Now turn this around. What is the smallest sum that a 6 can be in? Surely this is with 1 and 2 to give a smallest sum of 9. So the sums can only lie between 9 and 12 inclusive.
OK so how can we get 9? Do this systematically. If we used a 6 we’d have to make up 3 using two numbers. This can only be done with 1 and 2. If we used a 5 we’d have to make up 4 using two numbers. This can only be done with 1 and 3. (2 and 2 isn’t allowed.) If we used a 4 we’d have to make up 5 using two numbers. This can only be done with 2 and 3. (1 and 4 isn’t allowed.) So there are only three possibilities:
6 + 2 + 1; 5 + 3 + 1; 4 + 3 + 2.
There are only three sides to the triangle so we have them now. The only question is, which numbers go in the corners? But that is easy. These are the numbers that occur twice in the three sums. So we quickly get the four answers that we got by trial and error in the first session.
This method of proving that there are precisely four answers may be the nicest one of the lot. It certainly has a nice argument that shows that the sums are restricted to between 9 and 12 inclusive.
- A little bit of algebra.
Here we try to use algebra to see what progress can be made. We start by putting the letters a, b, c, d, e, f into the circles. As shown in the diagram below.
Suppose the sum along each side is s. Then we have the following equation:
3s = (a + b + c) + (c + d + e) + (e + f + a)
= (a + b + c + d + e + f) + (a + c + e)But the sum in the first bracket is 1 + 2 + 3 + 4 + 5 + 6 in some order, so that sum is 21. The sum in the second bracket is just the sum of the three corners. So we now have
3s = 21 + the corners.
But the smallest value of the corners is 1 + 2 + 3 = 6 and the largest value of the corners is 4 + 5 + 6 = 15. So we have
27 = 21 + 6 < 3s < 21 + 15 = 36.
So the sum has to lie between 9 and 12, just as we discovered in Method 4 above. But now we have a bonus, because the equation here tells us what the corners sum to. If s = 9, the corners sum to 6 and so are 1, 2, 3. If s = 10, the corners sum to 9 and so are 1, 2, 6; 1, 3, 5; or 2, 3, 4. If s = 11, the corners sum to 12 and so are 1, 5, 6; 2, 4, 6; 3, 4, 5. If s = 12, the corners sum to 15 and so are 4, 5, 6.
For s = 9 and 12, the answers now just fall out. For s = 10 and 11 there is a bit of work to be done but it is clear that with, for instance, 1, 5 and 6 in the corners, there is no way to get a sum of 11. So the work isn’t too hard and maybe easier than finding all ways to get 10. Whatever, we still end up with the four answers that we keep getting.
So where does this method lie in the ‘niceness’ stakes? It does rely on knowing a bit of algebra but once over that hurdle it gives the corner circle numbers pretty quickly and the rest of the numbers fall into place. The only small hold-up is the fact that we have to consider some corner numbers that don’t work; but maybe that’s a small price to pay. For sure it’s a lot better than Method 1.
Teaching sequence
- Recall the problem and discuss the conjecture that was made in the last lesson. How can we prove this conjecture? Note that it would be good to restrict the possible side sums. ‘How can we do this?’ Through discussion, lead them to some of the ideas that underlie the different proofs.
- In groups of 2 or 4, let them work on the ideas that they have generated. Our experience is that, with minimal scaffolding students can come up with the idea behind Method 4. You may need to help them along by asking ‘What is the biggest sum that 1 can be involved in?’ ‘What is the smallest sum that 6 can be involved in?
Any of the quicker groups should be encouraged to try to find another solution. - When a few groups have come up with a proof (possibly with your help), have a reporting back session. Let one of the students say what their group has come up with. Ask the rest of the class to test out what this student claims. ‘Is there anything that isn’t clear?’ ‘Is there any part that you don’t follow?’ ‘Is there any part that is wrong?’
- Give all of the class the chance to write up the proof in their own words.
- Show the class another way to prove that there are only four answers. ‘Which proof is best?’ ‘Which proof is ‘nicest’?’
- As an introduction for the next lesson, get them to think about how the problem might be generalised or extended. ‘What other problems can we make from this one?’ It’s at this point that experience from the V-sets Problem Solving unit will be valuable.
Session 3
Consider an extension of the Six Circle Problem – the Eight Circle Problem. Find all its answers and show there are no others.
Background
Here we look at a problem that is similar to the Six Circle Problem. Given the experience we’ve had with the Six Circle Problem we should be able to make some progress with this new problem. This problem is an extension of the Six Circle Problem.
The Eight Circle Problem: Is it possible to put the numbers 1, 2, 3, 4, 5, 6, 7, 8 in the circles so that the sums of the three numbers on either side of the square are the same?
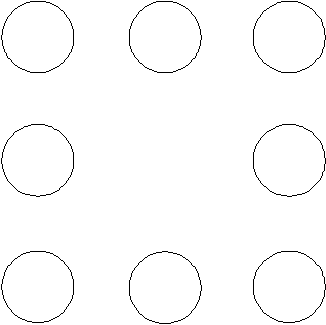
The techniques that we have used with the Six Circle Problem can be used again here. Any of the Methods that we noted in the proof of the four answer conjecture (see Background for Session 2) will work here. Clearly though, some are more efficient. For instance, if your students have a reasonable algebraic ability, we suggest that they try Method 5 to get the side sums. This method cuts down the number of options more effectively than looking at the biggest sum that 1 can be in. So, your class should find that the only possible sums are 12, 13, 14 and 15.
This problem takes a little more work than the Six Circle Problem but at the end, because your students will have approached it systematically, they will know that they have found all possible answers. Because of the extra work we suggest that your class works in groups of at least 4 and splits up the work between them.
In the end they should find a total of six answers. We list them below.
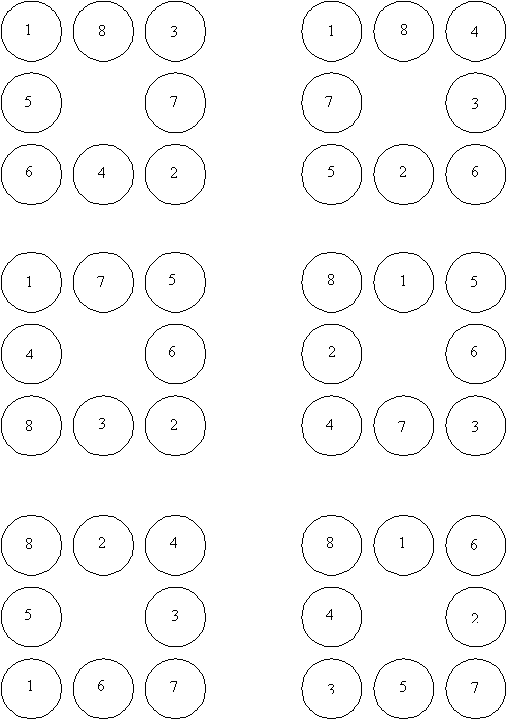
Teaching Sequence
- Get students to think about extensions or generalisations to the Six Circle Problem. Try to get several ideas from the class (some possibilities are to be found in this unit.) Lead them to the Eight Circle Problem.
- Follow the steps of Session 1 in letting them solve the Eight Circle Problem. This is harder than the Six Circle Problem so it may be useful if they divide certain parts of the problem up among themselves. Get them together when they think that they have most of the answers. Discuss how they might get the rest. Discuss how they might prove that there are only six answers.
Session 4
Generalise the Six Circle Problem by finding which sets of six numbers can replace 1, 2, 3, 4, 5, 6 and in balancing the sums on either side of the triangle.
Background
It’s now the time to generalise.
Problem: What other sets of 6 numbers can be put into the six circles below so that the sums of the numbers on each of the sides are the same?
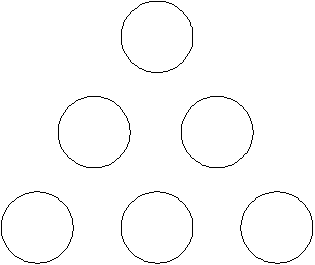
This is a generalisation of the original Six Circle Problem since when we find the answer, it will give us the answer to the original problem too. In this sense the Eight Circle Problem is not a generalisation because when it is solved it doesn’t immediately give us a solution of the Six Circle Problem.
Once again it’s a good thing to experiment. What can you come up with? Probably the fact that any six consecutive numbers will work is not too hard to see. Then maybe any six numbers that are the same distance apart like 5, 8, 11, 14, 17, and 20 will work. These can be thought of as any linear combination of 1, 2, 3, 4, 5, 6. This is because they can be written in the form {m + in: where i = 1, 2, 3, 4, 5, 6 and m and n are any whole numbers}.
But are these the only possibilities? What about {1, 2, 3, 4, 5, 100} or {1, 2, 3, 4, 5, 6, 50} or {1, 2, 3, 4, 5, 7}? Surprisingly the last one of these works to give two answers. So if we had a set like {a, b, c, d, e, f} how would we know that it would give us an answer or not? The trick here is to experiment and see what conjectures you can come up with.
And when you have done that you will start to see how many answers you get for each set. So then you can ask some more questions.
Can you find sets of numbers for which there is precisely one way to have the sums all equal? What can be said about such sets?
Can you find sets of numbers for which there are precisely two ways to have the sums all equal? What can be said about such sets?
Can you find sets of numbers for which there are precisely three ways to have the sums all equal? What can be said about such sets?
Can you find sets of numbers for which there are precisely four ways to have the sums all equal? What can be said about such sets?
But let’s look at the general problem first. We know already for the four answers that we got in Session 1, that
- The difference between opposite corner and middle numbers is the same. Look at A. 4 is opposite 1 and 4 – 1 = 3. 5 is opposite 2 and 5 – 2 = 3. 6 is opposite 3 and 6 – 3 = 3.
You should find that this is true for all possible correct ways to fill the six circles. The difference between opposite corner and middle numbers is the same. So take this and work with it a bit and turn it into a Conjecture.
Conjecture: A set of six numbers will correctly fill the six circles if and only if the set consists of three distinct pairs that have a common difference.
Just to check out what this means, the set of six numbers must be of the form a, a + d; b, b + d; c, c + d.
But how to prove this? Well, if we put a, b and c in the corners and their pairs in the opposite middle circle we get the configuration below.
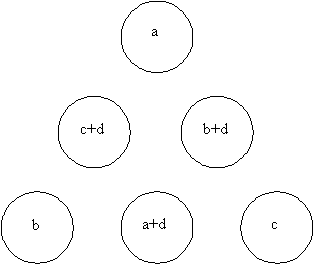
Then the sum of the three numbers on every side is a + b + c + d. So we get a legitimate set.
But what if we have a legitimate set? Can we show that it must be possible to arrange them in three pairs all with a common difference?
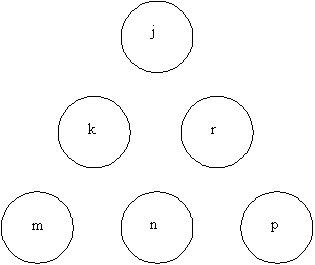
So let’s assume that we have an answer like the one in the diagram above where the six numbers are j, k, m, n, p, r. Because we have three equal sums, then
j + k + m = m + n + p = p + r + j.
Now j + k + m = m + n + p implies that j + k = n + p or that j – n = p – k.
And m + n + p = p + r + j implies that m + n = r + j or that j – n = m – r.
This gives j – n = m – r = p – k. So the set consists of three distinct pairs that have a common difference.
So now whenever we see six numbers we can tell whether or not we’ll be able to put them in the six circles so that the sums on each side of the triangle are the same.
Teaching Sequence
- Having considered an extension of the Six Circle Problem it is time to look at a generalisation. By discussion, lead them to think about what sets of six numbers might work in the six circles.
- Let them go into their groups to find other sets of six numbers that ‘work’. Encourage them to see what these sets have in common.
- You may need to bring the class back together to think about the sets they have found. Have they found any sets other than linear combinations of the original numbers? If not ask them to try {1, 2, 3, 4, 5, 100} or {1, 2, 3, 4, 5, 6, 50} or {1, 2, 3, 4, 5, 7}. ‘Can you come up with anything else?’
- Let them work on this for a while until they come up with a conjecture. Encourage them to prove the conjecture.
- Give them the opportunity to discuss their proofs in front of the whole class. Let them write up a proof.
Session 5
Discover and prove that in the six Circle problem there are only zero, two or four answers for any set of six numbers.
Background
Here we take up the questions of what sets give 1, 2, 3, or 4 answers. Again experimenting should be done to start with but the clue to the problem is to be found in the list of properties of the answers from Session 1. Remember, number 3 on the list says:
Changing corner numbers to the middle and vice-versa changes one answer into another. As the result of that it’s not too hard to see that the answers come in pairs. It’s a bit harder to see what sets give four answers but it turns out that four answers can only be obtained if the set is a linear combination of the numbers 1, 2, 3, 4, 5, 6.
Theorem 1. The answers from a set of six different numbers come in pairs.
Proof. Assume that the six numbers are a, a + d, b, b + d, c c + d and they are placed as we did above with a, b, c in the corners. Then it’s not too hard to see that we can form another answer with a, b, c in the middle circles and a + d, b + d, c + d respectively opposite them in the corners.
Theorem 2. A set of six numbers produces four answers if and only if the set is a linear combination of the numbers 1, 2, 3, 4, 5, 6.
Certainly if we have such a linear combination, we can make four answers by replacing i in the original four answers by m + in. You can check that the side sums are still equal. (Note that we can’t form more than four answers here because otherwise replacing m + in by i would give us more answers to the original problem.)
Suppose that the six numbers are a, a + d, b, b + d, c, c + d and that a < b < c. Then since we have another possible answer (other than the obvious one), a + e, for some possibly new value of e, will have to equal one of the other five numbers. Look at the possible 5 cases.
a + e = c + d: But since a is the smallest number any other number in the set plus e will be bigger than c + d. This is not possible.
a + e = b + d: Clearly d isn’t equal to e or a would equal b. There are now three possibilities: c + d = c + e; c + d = b + e; and c + d = a + d + e. The only one that leads anywhere is c + d = b + e when e = 3d and we get the linear combination a, a + d, a + 2d = b, a + 3d = b + d, a + 4d = c and a + 5d = c + d.
a + e = a + d: Here e = d and so c + d = c + e; c + d = b + e; and c + d = b + d + e. These all lead to contradictions or no progress.
a + e = c: Hence c + d = b + e; c + d = b + d + e; and c + d = a + d + e. These all lead to contradictions.
a + e = b: Hence c + d = c + e; c + d = b + d + e; and c + d = a + d + e. The only one that leads anywhere is c + d = b + d + e which gives d = 3e and the linear progression a, a + e = b, a + 2e = c, a + 3e = a + d, a + 4e = b + d and a + 5e = c + d.
So the only possibility for four answers is when we have a linear progression.
Teaching Sequence
-
First of all it is worth noting that there is a lot of work in this unit and you may want to drop some things out. We suggest that the proof of the four answer case may be one thing that could go as it is conceptually difficult. However, they can get at least as far as the conjecture that there are at most four answers for any set of six numbers.
-
Start the lesson by getting them to think about how many answers any set might produce. This might be done in a whole class setting or in their groups. As usual they should come up with a conjecture first and then try to find a proof of that conjecture.
-
Discuss their conjectures as a whole class and talk about what proof methods might be used.
-
When a proof has been found get a student to present it to the rest of the class. Let them criticise it. If no one is able to find a proof, even with your help, give a proof yourself. Let them criticise that. (It might be useful if you are doing this to out in an odd error to keep them on their toes.) Let them all write up a proof.
-
Review and discuss the results of the unit as a whole. What did they enjoy? What was hard?
Homelinks
(There are many answers to this question. You might want to restrict the different sums to being consecutive.)
We’ve been slaving hard this week on the Six Circles Problem. Your student will tell you what this is. So for a change let’s look at a situation where the sums aren’t equal. Can the numbers 1, 2, 3, 4, 5, 6 be put into the six circles below, so that the sums of the numbers on each side of the triangles are different? If they can, find all solutions.