This is a level 4 geometry strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (387 KB)
explore angle properties of two dimensional shapes
pattern blocks
FIO, Level 4, Geometry, Book One, Shaping Up, page 2
Copymaster of dodecagon
classmate
In these three activities, students explore the areas of pattern blocks relative to each other. They then consider the different ways in which a hexagon and a dodecagon can be made from pattern blocks. By doing this, they explore the behaviour of equivalent fractions.
Activity One
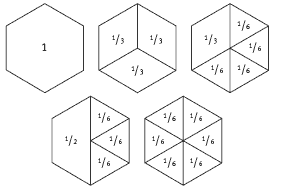
This activity involves regular hexagons. The students will soon discover that there are 7 ways of making a regular hexagon using the triangle, trapezium, and 60/120 pattern blocks (see the Answers), and from these, they should be able to write the various equations.
Activity Two
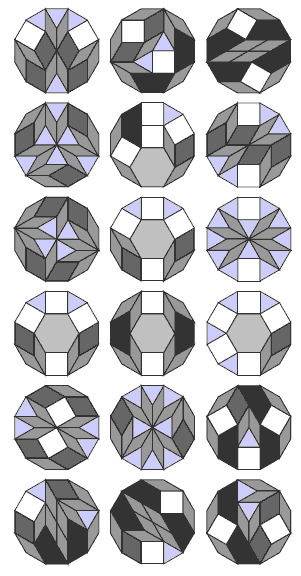
In this activity, the students make regular dodecagons that have sides that match the edge of the square pattern block. They shouldnÕt need any introduction to question 1. They will quickly find that there are many ways of using the various pattern blocks to complete the shape. The challenge for them will be to systematically record their solutions as tidy sketches.
In question 2a, the students write the sum of the area of the dodecagon as the sum of 3 different shapes, but, as they will discover in the following parts of this question, they can express it as the sum of just 2 shapes.
To do this, they must first show (in question 2b) that a square has the same area as 2 30/150 rhombuses. They may find it helpful to cut 2 rhombuses and a square from cardboard using the pattern blocks as templates. They can then overlay the rhombuses on the square. If they cut off the overlapping pieces, they can move these to fill the gaps on the square.
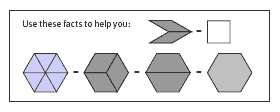
When doing questions 2e-f, the students need to use the equivalences they discovered in Activity One and in question 2b. (These are summarised in a panel in the Answers.) Using these equivalences, they can replace every 2 30/150 rhombuses with 1 square and every 6 triangles (or their equivalent) with 1 hexagon.
For the first dodecagon in question 1, the working could be set out like this:
Area = 4 squares + 4 30/150 rhombuses + 12 triangles
= 4 squares + 2 squares + 12 triangles
= 6 squares + 12 triangles
= 6 squares + 2 hexagons
As they do questions 2e-f, the students should come to see that the area of any of the dodecagons can be expressed as the sum of 6 squares and 2 hexagons. The area of each dodecagon is therefore the same.
Activity Three
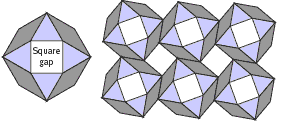
If we are trying to create a solid square (as implied), the answer to question 1 is "no". But it is possible to create a tessellation with square gaps in it. The Answers explain why and how.
When the students investigate question 1b, they will find that it is nonot possible to make either a regular octagon or a regular decagon using the pattern blocks.
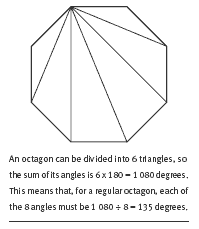
You may want to add to the explanation in the Answers by showing your class how to find the size of the interior angle of a regular polygon. One way is to first divide the polygon into triangles, as in the diagram. Because the 3 angles in a triangle have a sum of 180 degrees, you can multiply the number of triangles by 180 to get the
sum of all the interior angles of the polygon. (This works because all the angles of the triangles together make up the angles of the polygon.) The polygon is regular, so divide this total by the number of angles in the polygon to get the size of each interior angle.
Once again, for question 2, a useful strategy is to trace and cut 6 squares and 2 hexagons from cardboard. The hexagons can then be cut in half to form 4 trapeziums. When the trapeziums are overlaid on the squares, they do not completely cover them. This shows that the area of the squares is greater than the area of the hexagons.
Answers to Activities
1. Other ways are:
2.
1 = 1
1/2 + 1/2 = 1
1/2 + 1/3 + 1/6 = 1
1/2 + 1/6 + 1/6 + 1/6 = 1
1/3 + 1/3 + 1/3 = 1
1/3 + 1/6 + 1/6 + 1/6 + 1/6 = 1
1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1
Activity Two
1. There are many possible ways. Some of them are:
2. a. Area = 4 squares + 12 triangles + 4 30/150 rhombuses
b. Methods may differ. As a possible explanation, you could put 2 rhombuses on top of a square. Then you can see that the "spare" bits could be cut off and used to exactly fill the gaps inside the square. So the area of 2 rhombuses must
be the same as the area of 1 square.
c. Area = 6 squares + 12 triangles
d. Area = 6 squares + 2 hexagons
e.- f. Practical tasks. Use the facts that you have discovered in the earlier parts of this question (summarised in the panel below) to show that the area of every dodecagon can be reduced to 6 squares and 2 hexagons.
3. a. Although it still has 12 sides, the sides are no longer all the same length. It is, in fact, a semiregular dodecagon (semi-regular because there is a pattern to it).
b. Area = 12 squares + 5 hexagons. (The area of the dodecagon was 6 squares and 2 hexagons. To these, you have added 6 more squares and 6 trapeziums [the equivalent of 3 hexagons]).
Activity Three
1. a. No. To make a square shape you need right angles. With the exception of the square block and the 30/150 rhombus, the angles of all the blocks are 60o, or 120o, which by themselves will not form 90o.
You can, however, create a pattern that leaves a gap that is the size and shape of the square block. You can do this by making a semi-regular octagon from 4 triangles and 4 30/150 rhombus blocks. This octagon can be combined with others to form a tessellation featuring square gaps
b. A regular octagon needs interior angles of 135o (not possible) and the decagon 144o (not possible). The angles of all the pattern blocks are multiples of 30o. 135o and 144o are not multiples of 30o .
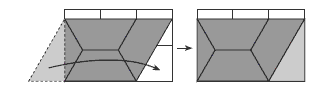
2. 6 squares have a greater area than 2 hexagons.
Here is one way of showing this:
2 hexagons have the same area as 4 trapeziums. Make a parallelogram from the 4 trapeziums and lay it on top of a 3-by-2 grid of squares, like this:
If the overhanging section of the trapezium on the left was cut off, it would exactly fit the gap on the right to make a rectangle. But this rectangle would be smaller than the rectangle formed by the 6 squares. (The difference is the narrow strip along the top.)