This unit of work provides students with the opportunity to discover the effect of a change of length by a given factor on area and volume.
- Use scale factors to investigate areas being enlarged.
- Use scale factors to investigate volumes being enlarged.
- Solve real life context problems involving scale factors.
The relationships between scale factors for length, area, and volume is conceptually difficult to understand. But it is also important and has some interesting practical applications. This unit introduces these ratios from a range of perspectives, and ends up looking at some practical applications. In addition the unit reminds students about the ways that mathematicians tackle and make progress with difficult problems. The emphasis in this unit is on students actively exploring the mathematics of a topic that is sometimes left to rote memorisation.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- modelling the enlargement of objects, in general terms, and in reflection of specific scale factors
- varying the complexity of scale factors you ask students to work with
- varying the complexity of the shapes students are asked to work with in session 3
- grouping students flexibly to encourage peer learning, scaffolding, extension, and the sharing and questioning of ideas
- applying gradual release of responsibility to scaffold students towards working independently
- roaming and providing support in response to students' demonstrated needs
- starting and ending each session with a review of key knowledge
- providing frequent opportunities for students to share their thinking and strategies, ask questions, collaborate, and clarify in a range of whole-class, small-group, peer-peer, and teacher-student settings.
Te reo Māori kupu such as taurahi (scale factor for enlargement), hoahoa āwhata (scale drawing, scale diagram), roa (long, length), and horahanga mata (surface area) could be introduced in this unit and used throughout other mathematical learning.
- Two balls, one with twice the diameter of the other
- Square tiles, cubes
- 8 identical regular tetrahedrons
- Photocopies of a prop (see session 1)
- Paper
Session 1
In this session the students are introduced to three areas of mathematics:
- the notion of scale factors for lengths and areas,
- the relationship between scale factors for length and area, and
- how mathematicians tackle and make progress with difficult problems.
Before class prepare two photocopies or a similar prop (perhaps something related to the culture, learning, or interests of your students). One photocopy is of your hand at its normal size and the second copy is of your hand enlarged by some whole number. For instance, if your hand (on the original copy) is 15cm long then the second image is either 30cm, 45cm, 60cm or 75cm.
- The following problem, which is used to begin the session, is large and wide-ranging:
If you take any 2-dimensional object, and enlarge it by a scale factor of f, by what scale factor is the area enlarged?
- Stated in this way the problem will probably be incomprehensible for most students. Some time will be needed to unpack its meaning. The following example should help make things clearer without unnecessarily spoiling the investigation that will follow.
- Show students the photocopies of your hand (or other prop). Discuss what the scale factor for enlargement is in this case (it is either 2, 3, 4 or 5 depending on the size of the image). Ask the following question (but don’t answer them):
By what factor do you think the area has been enlarged?
That is, if you need exactly one small jar of paint to colour the original hand, how many jars would be needed to colour the enlarged hand? (Adapt this as necessary)
Will it be the same as the scale factor for enlargement?
Important: The purpose of this discussion is to make sense of the original problem. It is not to answer it. We want the students to find the answer for themselves, later.
Emphasise: this is a difficult problem; you are going to show them how a mathematician would approach such a difficult problem; and you are going to show them how to be mathematicians.
- Once you are clear that the students understand the problem, discuss how it might be investigated.
How should a difficult problem such as the original one – an unspecified object is enlarged by an unspecified amount and the impact on the area is required – be approached?
Hopefully at least one person will come up with the idea of solving a simpler problem first. This should lead to a discussion of what might a simpler problem be in this situation, and of situations in which scale enlargements are used. Acknowledge that it is far from obvious which of the many simplifications would be productive in this situation. Mathematicians struggle over these sorts of things, so it is important not to pretend that things are immediately obvious. It is OK to be unsure how to proceed. It is OK to not know exactly which simpler problem is best for making a start. A bit of trial and error with a range of possible simple problems is the usual way to begin.
- Make a list of some possible simpler problems. Discuss what ‘to simplify’ means in this situation.
Which aspects of the problem can be simplified?
Can two aspects be simplified at the same time?
What real-life contexts do you think these aspects (e.g. enlargement) would be used in?
- In the present problem, a useful simplest starting point is to begin with a simple regular shape and investigate what happens to the area when it is enlarged. Students often suggest using a circle as a simple starting shape. Suggest putting case to one side for the moment, as it is harder than it looks.
- Suggest using a square to start with. The simpler problem becomes:
If you take any square, and enlarge it by a scale factor f, by what scale factor is the area enlarged?
An even simpler problem is:
If you take any square, and enlarge it by a scale factor 2, by what scale factor is the area enlarged?
If this is solved the scale factor 3 could be investigated next. Then the scale factors 4, 5, 6, and so on.
- Discuss how the simplest problem might be approached. Guide discussion to read the suggestion of an approach of the sort shown in the diagram below.
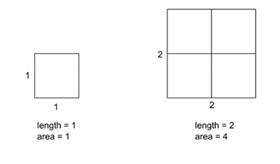
- Once students are clear about this method of approach set them the task of investigating other simple problems using this method, or another of their choice. It might be useful to issue some students with a pile of square tiles. The number of tiles used to make a square can be taken as the measure of the area. The length of the tile can be taken as the equivalent unit of length. Other students can draw squares on paper and achieve the same ends.
- Once the students have worked on this for a while see if they can make a conjecture of the form: ‘If a square is enlarged by a factor of f, then the area will increase by a factor of …’. Discuss whether or not this conjecture can be proved and if so, what would be suitable as a proof.
- Following this, discuss the issue of counter-examples.
What might be counter-examples in this case?
For instance, what happens in the situation where f is not a whole number? What if f is 0.5 or 1.5, for example?
Can the students show using pictures of the sort used in Diagram 1.1, that their conjecture holds in these cases too?
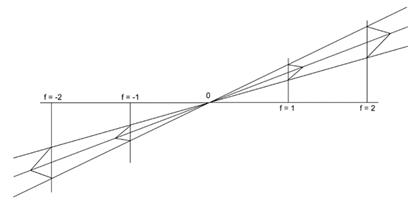
- If the students raise the issue of negative scale factors, this will need to be dealt with. Show them, using a projection diagram of the sort shown in the diagram below, what a negative enlargement is, and then get them to investigate the problem for negative scale factors. With a negative scale factor the image and the figure are on opposite side of the centre of enlargement.
- Ask: What if a different ‘simple shape’ were used?
Another good example is an equilateral triangle. Ask the students to investigate this particular shape for a variety of integer and non-integer scale factors. See for instance the diagram below.
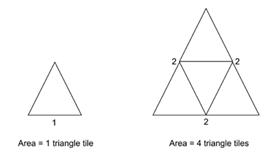
- In this situation a small tile shaped as an equilateral triangle is taken as a unit of area.
What about triangles that are not equilateral?
- Finally, discuss:
- why a circle may not be a good choice as a ‘simplest shape’? [because circles do not tessellate]
- what progress has been made on the initial larger problem?
- which aspects of the initial problem have yet to be addressed (what if the initial shape was an irregular blob, for instance?).
Session 2
In this session the work begun in the previous session is extended and consolidated.
- As a warm-up, get the students to investigate the situation where the simple special case is a rectangle. There is a possible counter-example that the students may not have identified.
What if the initial figure has a hole in it? (as in the diagram below)
What happens then?
Do the results that have been conjectured and/or proved in the previous session hold in this case?
If so, why? If not, what happens in these cases?
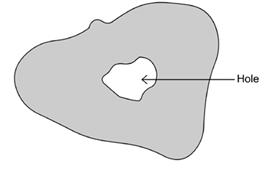
- Set the students the task of investigating this situation in a careful and systematic manner – using simple cases and so on – in the way used in the previous session. Their first task will be to decide what the simplest case is in this situation.
- This will take quite a while. Some students will find that they will need to revisit the ideas they covered in the previous session because they are unable to use them in this new situation.
- Once students have made some useful progress on this, shift the discussion to the case of the circle.
How can this be investigated?
- Open this for discussion. Two ideas are certainly worth fuller discussion and further investigation.
The first is that the area of a circle can be determined by knowing only one fact about the circle concerned: the length of the radius. So if we know what happens to the radius under an enlargement, we can then determine what happens to the area. Set the students the task of carefully investigating this situation. They should fully explain and justify their results.
- The second involves an introduction to a trick that mathematician sometimes use. It does not produce a hard and fast result, but it helps us think about the problem in a new way. Show the students how a circle can be converted to something that is very nearly a rectangle. See the diagram below.
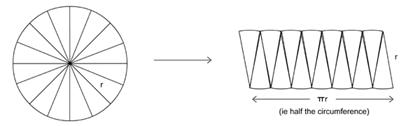
- This is worth taking some time over. It is useful to literally cut a circle into sectors and form a kind of rectangle (or parallelogram). But this is not enough. The students need to be encouraged to imagine what would happen if the same process was undertaken for larger and larger numbers of sectors (100 sectors, 1000 sectors, and so on). Encourage them to engage with the idea that the more sectors that are used the closer the circle comes to a rectangle.
- Ask: What happens when a circle is enlarged?
Imagine the circle is transformed into a ‘near rectangle’ using 1000 segments, and the rectangle is enlarged. We have just seen, at the start of this session, that, in the case of a rectangle, the scale factor for area is squared. Of course this result is only approximate for the circle.
What if 10 000 segments were used?
The same process can be undertaken, and again the result would only be approximate. But it would be a better approximation.
What if 100 000 segments were used?
- Discuss this. The purpose of the discussion is to introduce the idea of getting closer and closer to a limiting case. It is not necessary that students fully understand this situation. But it is useful to get them thinking along these lines in preparation for them encountering these ideas in future years.
Session 3
In this session the work begun in the first session is extended and consolidated, but this time in a different direction: surface area and volume.
- In this case, the starting problem is this:
If you take any 3-dimensional object, and enlarge it by a scale factor f, by what scale factor is the surface area enlarged?
By what scale factor is the volume enlarged?
- As in the first session it is useful to give an example that establishes the meaning of the problem. Bring into the class two balls, one twice the size (diameter) of the other. Discuss what the notion of surface area refers to (it is the amount of material needed to cover the ball).
Will the surface area of the larger ball be twice that of the smaller one?
- Discuss what the notion of volume refers to (if the ball were to be filled with fluid, how much fluid would be needed?)
Will the volume of the larger ball be twice that of the smaller one?
It is also important to establish that the meaning of enlargement is clear in the 3-dimensional situation. Take the case of a cuboid. If this were enlarged by a scale factor of three, ensure the students are clear that this results in a cuboid that is three times the length, the width and the height. Or, take the case of a can of paint. If this were enlarged by a scale factor of two, ensure the students are clear that this results in a can that is both twice as long and with twice the diameter.
There may be students who would prefer to tackle such problems using the formula for the surface area and volume of a sphere or cylinder. This is fine in principle, but explain that the approach used here is different because you are also teaching the students to solve difficult problems by first solving simpler cases.
- The simplest case in this situation is the small unit cube. It is useful to make available a pile of small cubes so that students can build up cubes that are twice and three times the size, and then count the new surface areas and volumes. Set the students the task of investigating the scale factors for surface area and volume when a cube is enlarged. Encourage the students to approach the investigation carefully and to fully explain their results.
- Present the class with 8 identical regular tetrahedrons. These can be made in advance by the students using a cardboard net made up of four equilateral triangles with appropriately placed tabs for gluing purposes. Select a group of 3 students to come in front of the class and try and put them together geometrically to form a regular tetrahedron that is twice the size of each. Give them a set period of time (say 1 minute). If they do not succeed in the set time, select another group to see if they can. Continue this until the problem is either solved or the students become convinced that it is insoluble. Discuss the lessons that can be learned (about solving simpler problems first) from the activity.
- Imagine a tall and athletic adult man. Estimate what his height would be. Estimate his weight. Estimate the cross-sectional area of his main lower leg bone. Fix on specific and realistic values for each of these. Now calculate what the weight and cross-sectional area of the lower leg bone of a man who is an enlargement by a scale factor of two of the original man. Get the students to show why humans cannot grow larger and larger and that at some point the enlarged human bones would no longer be strong enough to carry the weight of the enlarged body.
What are the implications for this finding? [Hint: think about the ration of weight to leg bone cross-sectional area under enlargement.]
Session 4
In previous sections the problems were presented in such a way that the scale factor for enlargement of length was the starting point, and on this basis the scale factors for area and volume were calculated. In this session this situation is reversed. In addition, this session should help students to realise that we can easily be fooled – in advertising, for instance – by two dimensional representations of three dimensional objects.
- Set the students this problem: Draw two different sized squares. The larger is to have double the area of the smaller.
- This is a non-trivial problem. Some students will quickly see how it can be approached. Others will need time to think it through. Typically a great deal of trial and error will be used. A systematic approach might involve the strategy of working backwards.
- Take a square and enlarge it using scale factor s. The scale factor for area is found by squaring the scale factor for length. Thus the scale factor for area is s2. If this is reversed, a method is provided for solving the problem being investigated. The scale factor for area is 2. The scale factor for length is found by taking the square root of 2. Thus the scale factor for length is √2.
- As an informative and related activity, give each student (or group of students) two identical squares of paper. Instruct them to cut each square along a diagonal and calculate the length of the diagonal. Now get them to combine the four triangles to make a single larger square.
What is the area of the larger square?
What is the length of the side of the large square? Why?
How is this connected to the above problem? Is there a way of doing a similar thing by starting with 4 individual squares?
What if you start with 3 individual squares; can these be cut and combined to form a larger square?
- Set the students this problem. Draw a small poster that shows two different sized balls (e.g. soccer balls or netballs, note that this could be adapted to reflect a more relevant context). The larger ball needs to have double the volume of the smaller ball.
- Get them to explain how advertising agents could fool us, using diagrams such as these, into gaining the wrong impression from a picture used in an advertisement. Construct and draw an advertisement for some product or service that illustrates how scale factors can be used to mislead. [For instance, by showing two circles—one with twice the diameter of the other—to represent a doubling (of a financial return, for example). But visually we tend to ‘see’, not the diameters in the ratio 1:2, but the areas; and the areas are in the ratio 1:4. The diagram is thus likely to mislead.]
Session 5
In this session the ideas developed in earlier sessions are brought together to deal in a systematic way with two practical problems in the study of mammals (you could adapt this to look at native species or mammals that are relevant to your learning). The first involves the relative rates of heat loss for two sea mammals of similar shapes but different sizes (a whale and a dolphin, for instance). The second basically asks the question: Can land mammals increase in size without a problem? In other words, is there any reason why elephants, for instance, could not be twice the size they are now?
- Students should be grouped and asked to investigate each of these from scratch using the techniques introduced in earlier sessions.
- In the first problem the rate of heat loss is the ratio of surface area to volume. Students need to investigate simple cases.
What is the ratio for a single cube?
What is the ratio for a cube of size 2, and so on?
Graphing the ratio as it changes would also be useful. It is important that they spend time discussing and identifying the consequences of their findings for the study of sea mammals.
- In the second problem the important issue hinges around the strength of bones such as the leg bone. The strength of the leg bone can be taken as proportional to the cross-sectional area of the leg bone. Thus the crucial ratio is that of volume to cross sectional surface area. Looking at simple cases reveals that, for a cube of volume 1, the cross-sectional area is 1, and the ratio is 1. For a cube of volume 8, the cross sectional area is 4, and the ratio is 2; thus the cube of volume 8 is under twice the stress as in the single cube. Again, graphing the ratio is revealing. And again, students should spend time discussing and identifying the consequences of their findings for the study of large mammals.
Dear families and whānau,
Recently we have been learning about scale factors for the enlargement of area and volume. Ask your child to share their learning with you.