Sandwiches

The Problem

Ngawai and Tom make a peanut butter sandwich. How can they share it fairly?

Can you find three different ways to cut the sandwich?

Lesson Sequence

1. Introduce the problem using a peanut sandwich and two students from the class.
2. Ask the students to all think of one way that they could share the sandwich. Share one idea.
3. Read the problem to the class.
4. Solve the problem in pairs. As the students work, ask questions that focus on the meaning of a ½. Allow the students to describe their ideas. Encourage explanations.
   How do you know the parts are equal?
   Are you happy with your share? Why?
   Can you think of other ways to share it?
   Tell me about your thinking?
   How are you keeping track of the ways that you find?
5. Ask that the students keep a record of the different ways that they find to share the sandwich.
6. Share solutions.

Extension

Imagine a loaf that does not have a square cross-section.
Use 4 students instead of 2.
Share a bag of 8 lollies between Ngawai and Tom.

Other Contexts for the Problem

Giant chocolate chip cookies (circular region)
Working space on a desk

Solution

There are, in fact, an infinite number of solutions. As long as you cut or fold through the centre point of the rectangle the parts will be equal. Some examples of single cuts or folds are:

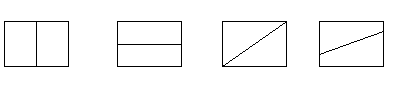
In order to see that all of these cuts do give equal parts, it is enough to put one on top of the other. This may require rotation in some cases. This may provide the opportunity to explore some of the transformation ideas from the Geometry Strand.

If the bread has a cross-section that consists of a rectangle with a semi-circle on top, then there is only one simple solution to the problem by making a vertical cut. There must be another solution by cutting parallel to the base of the rectangle (the side opposite the semi-circle) but it is extremely difficult to find the exact point to make this cut.

Solution to the Extension:

To produce four equal parts is a little more difficult. In the first two drawings above, a second cut perpendicular to the first cut and through the centre will work. As for the other drawings, many solutions exist but in practice they are hard to find.

Lollies are somewhat easier. Four each is the answer here.