In this unit a number of small boxes are produced (by folding), that fit inside one another like Russian dolls. Lengths are measured and areas and volumes are calculated in order to make scale comparisons.
- Find the scale factors for length, area and volume.
- Identify the center point of an enlargement.
- Place similar objects to show a negative enlargement.
Enlargement is a transformation that changes the size of a figure or 3-D shape.
The starting figure is called the object and the enlarged shape the image. The object and the image are the same shape but different sizes and are said to be similar figures.
The scale factor connecting the object with its image is usually denoted by the letter k and calculated by comparing features of the object and image.
k = length of image side
length of object side
If k > 1 then the image is larger than the object
If k = 1 then the image is the same size as the object
If 0 < k < 1 then the image is smaller than the object
Negative scale factors
The image and the figure are on opposite sides of the centre of enlargement.
Properties of enlargement
- The centre is of the enlargement is the only invariant point
- Angle size is invariant
- Length, area and volume are changed
- Enlargement is a direct transformation
Scale factor for area and volume
If k is the scale factor for an enlargement then
k 2 is the scale factor for the area and
k 2 = area of object
area of image
k3 is the scale factor for the volume for this transformation
k3 = volume of object
volume of image
Getting started (Session 1)
- Tell the students they are going to construct four different sized open boxes, using a square of cardboard. The red one uses a 5cm x 5cm square, the green one a 10cm x 10cm square, the pink one 15cm x 15cm and the biggest one, black uses a 20cm x 20cm starting square. This can be completed as a group task with each student making one box or in pairs with each student making 2 boxes as part of the four box set. Copymaster 1 gives a template for the smallest three squares fitting on an A4 page. The 20cm x 20cm will need to be cut from a larger page.
- Get the students to cut out from the templates, or measure, the square pieces of card making one set of four per group. Each student can fold one box
Once you have measured the length of one side how can you fold the card to get another equal side?
Fold the card along both diagonals to identify the middle of the square - Folding instructions to produce an open box:
- Fold each of the four vertices (corners) of the square into the middle point and leave them there.
- Fold the top and bottom edge into the middle then unfold.
- Repeat this, folding the other two edges into the middle then unfold. With the four vertices still folded into middle point you should now have a square made up of 16 smaller creased squares.
- Make a small vertical cut, one square in, on both the right and left of the bottom edge the length of one square. Repeat this on the top edge.
Cut on the top and bottom edge only.
Copymaster 2 shows how the cuts and folds will look on the opened out piece of original cardboard. - Carefully open out and lie flat the pointed flaps that lie between the two cuts you have made on the top and the bottom edge.
- Crease the two squares left on the bottom edge into the middle. Repeat for the two squares left on the top edge.
- Holding the two bottom squares between thumb and forefinger fold then up together to form the sides of the open box.
- Pull the flap up and over the edge formed by the two squares; allowing the point to met in the middle of the base of the box.
- Repeat g) and h) for the top squares and flap.
- The four vertices (corners) of the original square of card should met at the centre point of the base covering the inside base of the open box.
- Encourage the students to make conjectures about the relationship between their box and the original cardboard square as well as between box comparisons.
What is the relationship between the ‘size’ of your box and the size of the square card it was made from?
Estimate how many of the bases of your open box would fit into the original cardboard square?
How does your box compare with the other three boxes made in your group?
- Get the students to carefully measure the height of the box, the length of the base of the box, the diagonal of the base of the box and any other measurements they think may be relevant.
- Bring up calculating the area of the base and the volume of the open box if this is not suggested by the students.
- Record Your Results
Make a heading for this investigation in your class book and copy and complete this table of measurements for your boxes.
Measurements should be as accurate as possible (to the nearest mm) – eg 2.1 cm, 5.6 cm.
|
Box
|
Size of Card
|
Base Diagonal
|
Length of Base
|
Height of Box
|
Area of Base
|
Volume of Box
|
|
Red
|
5 cm x 5 cm
|
|
|
|
|
|
|
Green
|
10 cm x 10 cm
|
|
|
|
|
|
|
Pink
|
15 cm x 15 cm
|
|
|
|
|
|
|
Black
|
20 cm x 20 cm
|
|
|
|
|
|
The Investigation (Session 2)
- Ask students to investigate scale factors by comparing the side length, the base area and the volume of the various sized boxes they have made.
Remind them to record their results carefully as they go. - Firstly, ask the students to consider length. It is useful to remind them to check any assumptions for both side length and diagonal length
Use the Red Box as the original object.
Encourage them to manipulate the boxes to estimate the answers then confirm them using the measurement in their table (session 1). The measurements may not lead to the exact scale factor and a discussion of the inaccuracies involved in measuring is useful.
How big is the length of the base of the green box compared to the red box?
What is the scale factor for enlargement for the red box going to the green box?
What is the scale factor for enlargement for the red box going to the pink box?
Is this the same scale factor for the area of the base, the volume? - Once they have established that there are differences in the scale factors between length, area and volume, and then ask the students to focus specifically on the area.
Compare the area of the base of the Green and Red boxes. What do you notice?
What about the area of the base of the Pink and Red boxes?
What about the area of the base of the Black and Red boxes?
What is the scale factor for the area of each of these boxes compared to the smallest Red box?
Can you find the scale factor for the base area, for the enlargement that takes the Green box to the Black box? the Green box to the Pink box?, the Pink box to the Black box? - Ask students to summarise their results so far. Encourage them to record their results in an organised way identifying key ideas as they carry out the investigation in preparation for their poster presentation.
How does the area factor relate to the original scale factor (length) for the enlargement? - Next ask the students to focus on comparing the volumes of the four boxes.
Estimate how many of the red boxes would fit inside the Green box? Check it out. What do you notice? Look at the results in your measurement table. Do they confirm what you think?
What about the volume of the Pink and Red boxes?
What about the volume of the Black and Red boxes?
What is the scale factor for the volume of each of these boxes compared to the smallest Red box?
Can you find the scale factor for the volume, for the enlargement that takes the Green box to the Black box? the Green box to the Pink box?, the Pink box to the Black box? - Summarise the volume results
How does the volume factor relate to the original scale factor (length) for the enlargement? - Encourage the students to explore any thing else that interests them.
What else can you find out? - You could choose to focus the students on the reverse transformation – the reduction with a scale factor less than one. (This may be used as an extension for the faster finishers)
What about the other way, where an object is reduced by the enlargement?
What is the scale factor that would take the Black box back to the little Red box? the Pink box to the red box?, the Green box to the Red box?
What about in between connections –like the Black box back to the Pink or Green box? etc
What would be the area, volume scale factors here?
Centre of Enlargement and Negative Enlargements (Session 3)
- The students will be using their group’s four boxes to explore the affect of using different centers of enlargement as well as negative enlargements. They will be placing the boxes in various positions to represent enlargements with different centers and scales.
Remind them you are talking about the scale factor for enlargement (length) and focusing here on the correct placement of the boxes relative to the various centres. Avoid confusion with the previous session about scale factors for area and volume. (You can still reinforce the area and length scale factor work with reminder questions about comparisons between the box base areas and volumes.) - Ask the students to place their boxes one inside another, like the Russian Dolls, and identify where the centre of enlargement would be by placing a coloured pin at the appropriate place. Tell them to sketch a 2-D diagram of their placement of the boxes showing the base positions and the centre pin.
Can you do this in two different ways? - Get the students to model various enlargements using the different combinations of boxes with the coloured pin as the centre of the enlargement.
Place the Red box on some blank A4 paper and place the coloured pin somewhere outside of the box. Use this as the centre of enlargement. Decide on the appropriate distance and the appropriate coloured box to use to accurately show an enlargement of scale factor 2,3,4 - Tell the students to place the pin in a different position outside of the Red box.
How does the position of the pin affect the final diagram? - Then get them to explore a range of starting boxes with different positions for the centre of enlargement.
Starting with the Green box as the object and any centre position where would you place the Pink or Black box to be consistent with the appropriate scale factor? - Challenge the students to present you with an interesting example using a non whole number scale factor.
Remind them to record in diagrammatic form a number of their explorations.
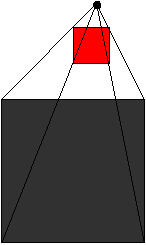
- Negative scale factors may have emerged out of the exploration above. If not ask the students to consider the case where the image is on the opposite side of the centre of enlargement. Model this with two of the boxes eg. Red box and Green box showing a placement of the Green box given a centre of enlargement and the position of the Red box (the object). This represents an enlargement with a scale factor of negative 2.
Label each of the vertices of the boxes to ensure the students appreciate that the boxes are also doing a half turn.
How would different centers of enlargement effect the position of the Green box?
Can someone model an enlargement using a negative 3 scale factor? - Ask the students to draw a simple picture inside the box them ask them what will happen to the picture on the base of the box after the negative enlargement.
- Get the students to model at least two other cases using a negative scale factor and different centres.
Review (Session 4)
- Discuss the boxes, highlighting key results.
- Students could summarize their findings in poster form. This may be done as a group or pair task depending on you class arrangement. The poster should show their understanding of:
- Scale factor for enlargement
- Area scale factor
- Volume scale factor
- Negative enlargement
- The effect of different centers of enlargement
- Any other important results you have discovered.
- Reinforcement problems involving enlargement and scalefactor, such as those found in textbooks and/or worksheets could be assigned or written on the board.
Calculate the scale factor that is used to calculate the sizes of the planets based on your choice of model size for the sun.
Consider the mass (volume) of Mercury, how much larger is the mass(volume) of the Earth? Do not calculate the volume of Mercury but use your knowledge of scale factors to find how much bigger the Earth is.
Explore the diameter and volumes need for other scale models of the solar system
Fold the measured side to the other side over the diagonal and cut along the other two sides.
Useful estimates could relate to side length of the boxes compared to original length of the cardboard or base area compared to original area of the cardboard. Allow the students to discuss what they mean by “size”. Hopefully length, area and volume will all come up.
|
Box
|
Size of Card
|
Base Diagonal
cm
|
Length of Base
cm
|
Height of Box
cm
|
Area of Base
cm2
|
Volume of Box
cm3
|
|
Red
|
5 cm x 5 cm
|
2.5
|
1.7
|
0.9
|
2.9
|
2.6
|
|
Green
|
10 cm x 10 cm
|
5.0
|
3.5
|
1.8
|
12.3
|
22.1
|
|
Pink
|
15 cm x 15 cm
|
7.5
|
5.3
|
2.7
|
28.1
|
75.8
|
|
Black
|
20 cm x 20 cm
|
10.1
|
7.0
|
3.6
|
49.0
|
176.4
|
Length scale factors
| Length Scale Factor IMAGE BOX | |||||
|
OBJECT
BOX
|
Red | Green | Pink | Black | |
| Red | 1 | 2 | 3 | 4 | |
| Green | ½ | 1 | 3/2 | 2 | |
| Pink | 1/3 | 2/3 | 1 | 4/3 | |
| Black | 1/4 | 1/2 | 3/4 | 1 | |
The base area of the green box is four times the base area of the red box.
| Base Area Scale Factor IMAGE BOX | |||||
|
OBJECT
BOX
|
Red | Green | Pink | Black | |
| Red | 1 | 4 | 9 | 16 | |
| Green | 1/4 | 1 | 9/4=2.25 | 4 | |
| Pink | 1/9 | 4/9 | 1 | 16/9=1.78 | |
| Black | 1/16 | 1/4 | 9/16 | 1 | |
The area scale factor is the length scale factor squared
k 2 is the scale factor for the area and
area of image
Green box area 3.5 x 3.5 = 12.25 cm2
and 2.89/12.25 = 4.24 or to 1dp 12.3/2.9 = 4.2
so 4.2 approx area scale factor, but 4 exactly by considering the physical model and the fold lines.
| Volume Scale Factor IMAGE BOX | |||||
|
OBJECT
BOX
|
Red | Green | Pink | Black | |
| Red | 1 | 8 | 27 | 64 | |
| Green | 1/8 | 1 | 27/8 | 8 | |
| Pink | 1/27 | 8/27 | 1 | 64/27 | |
| Black | 1/64 | 1/8 | 27/64 | 1 | |
If k is the scale factor for an enlargement then
k3 is the scale factor for the volume for this transformation
volume of image
Red to black volume scale factor – 176.4/2.6 = 67.8 = 68 (nearest whole number: nwn) which confirms the 64 times established by the physical model.
Red to pink – 75.8/2.6 = 29.2 = 29(nwn), which confirms the 27 times established by the models.
The reduction scale factors – see the table above
They may consider what the negative enlargement would look like.
See the reductions in the three tables above.
The length, area volume scale factors are just inverted for the reductions.
Consider the center pin either at one corner of the box or in the middle.
They may consider an infinite number of alternative positions for the pin inside the starting object square
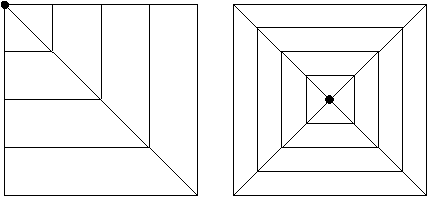
Center at one corner Center in the middle
Scale factor 2, center outside the red box - red with green box
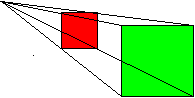
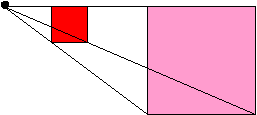
Green to pink box SF = 3/2
The distance between the centre of the enlargement and each of the vertices on the pink box is 1 ½ times the distance between the centre of the enlargement and each of the vertices on the green box.
The distance between the centre of the enlargement and each of the vertices on the black box is twice the distance between the centre of the enlargement and each of the vertices on the green box.
The distance between the centre of the enlargement and each of the vertices on the black box is 1 1/3 the distance between the centre of the enlargement and each of the vertices on the pink box.
Different centers means the length between the centre and the object is different hence the length to the image is increased when this different amount is multiplied by the relevant scale factor. The negative scale factor still meant the image box is on the opposite side of the centre of enlargement.
When observing the students performing the negative enlargements check for the inverted pictures in the image boxes.
Any other combinations can be considered. Look for careful measurements of the distance between the centre of enlargement and the vertices of the base of the object box and the use of the appropriate scale factor to calculate the new distance between the centre of the enlargement and the corresponding image vertices.