This problem solving activity has a geometry focus.
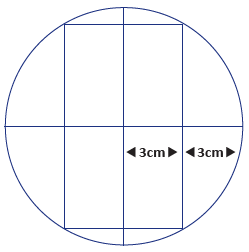
The High Peak Jewellery Company wants a new logo. Martin has come up with one based on a ring and a diamond. It is constructed by inscribing a rectangle in a circle as shown below.
The diamond is then drawn inside the rectangle.
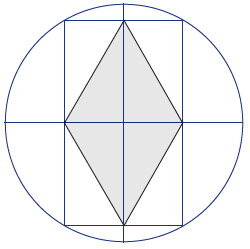
Can Martin construct the shape using only ruler and compasses? What is the area of the diamond shape?
- Use Pythagoras’ theorem to find the area of a rhombus.
- Use rulers and compasses to make a construction requiring perpendicular bisectors.
- Devise and use problem solving strategies to explore situations mathematically (be systematic, draw diagram).
This geometrical problem involves the application of standard constructions. This should support students to see how to solve the area aspect of the problem. At first it appears that there is insufficient information for a solution to be found, however, in such cases a diagram can be a useful tool to enable students to proceed.
Note: A number of problems appear to have insufficient information, including the Level 6 Number and Algebra (Equations and Expressions) problem Pigs, Goats and Sheep. In this case, the fact that whole numbers were involved meant that extra necessary information could be derived.
The Problem
The High Peak Jewellery Company wants a new logo. Martin has come up with one based on a ring and a diamond. It is constructed by inscribing a rectangle in a circle as shown below.
The diamond is then drawn inside the rectangle.
Can Martin construct the shape using only ruler and compasses?
What is the area of the diamond shape?
Teaching Sequence
- Show the students the logo and ask them to describe it. Encourage them to use geometric terms (bisect, rhombus).
What would you need to construct this?
Where would you start? What next? - Pose the problem for the students to work on.
- Questions that can help the students get started include:
What information do you know?
What mathematical knowledge could you apply to this problem?
What can you tell me about the radius of the circle? - As the students work on the problem ask questions that focus on their construction skills and their application of Pythagoras.
What do you need to know to work out the area of the rhombus?
What can you tell me about the side length of the rhombus? - Ask the students to list the steps they took in solving the problem that they believe are important steps that need to be followed.
- Share lists of steps taken. Discuss the similarities and differences in approaches taken.
Extensions
A circle is inscribed in the rhombus. What is its area?
Invent your own logo for The High Peak Jewellery Company.
Solution
To construct the logo Martin has first to draw in the circle. That is straightforward. Now draw in any diameter through the centre of the circle. To get the point which is 3 cm from the centre and the circumference use the normal method of producing the perpendicular bisecting a line segment. Then extend the perpendicular bisector if necessary to cut the circle at two points. Repeat the process on the other side of the centre. Now join the four points on the circle to make the rectangle. Finally join up the points to make the rhombus.
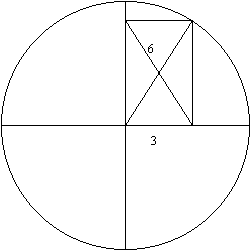
The key to finding the area is to see that the side of the rhombus equals the radius of the circle, since the diagonals of a rectangle are equal. Thus, using Pythagoras’ Theorem, the other side of the triangle is
62 = a2 + 32
27 = a2
√27 = a
3√3 = 27
Hence the area is half the base times the height = 0.5 x 3 x 3√3. This is approximately 7.79 cm2.
Solution to the Extension
To find the radius of the circle inscribed in the rhombus, note that the radius of this circle is perpendicular to the side of the rhombus.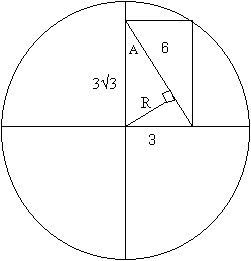
Now Sin A = 3/6 using the larger triangle and Sin A = R / (3√3).
Therefore R / (3√3) = 3/6
Giving R = (9√3)/ 6 or 2.6.