Pythagoras' Theorem

Session 1

In this session we look at the history of Pythagoras, introduce the theory, and look at the 3,4,5 triangle using cuisenaire rods.

1. Introduce the subject of Pythagoras, ask if anyone knows anything about him; when he lived or what he might have done.Give a brief explanation (below).

Pythagoras of Samos lived from about 569 BC to about 475 BC, he was a Greek philosopher who made important developments in mathematics, astronomy, and the theory of music. He spent most of his life in the Greek colonies in Sicily and southern Italy. He never married, but he had a group of followers who followed him around and taught other people what he had taught them. The Pythagoreans were known for their pure lives (they didn't eat beans, for example, because they thought beans were not pure enough). They wore their hair long, and wore only simple clothing, and went barefoot.

Pythagoreans were interested in philosophy, but especially in music and mathematics, two ways of making order out of chaos. Music is noise that makes sense, and mathematics is the whole world reduced to rules.

Pythagoras himself is best known for proving that the Pythagorean Theorem was true. The Sumerians, two thousand years earlier, already knew that it was generally true, and they used it in their measurements, but Pythagoras proved that it would always be true.

2. Write up Pythagoras’ Theorem on the board and ask the class to try to explain it.
    

This may require some revision of knowledge of geometry.  What is a right-angled triangle?  (A triangle with 90⁰ as one of its interior angles)  What does hypotenuse mean?  (The longest side of a right-angled triangle, which is always the one opposite the right angle)  Also ensure that the class understands what the square of a number is (The result of multiplying the number by itself, eg. the square of 4 = 4x4 = 4² =16), and what the sum of two numbers means (Add them together).  Explain that the theorem is often stated as a²+b²=c², where a and b are the short sides and c is the hypotenuse. 

3. Get the class to help rewrite Pythagoras’ Theorem so it makes sense to them, eg.  If you take the length of the longest side of a right-angled triangle and square it, you will always get the same amount as you get if you square the lengths of the other sides and then add them together.

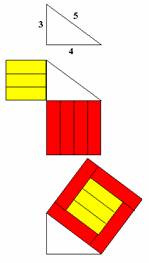
4. Demonstration of Pythagoras’ theory for 3, 4, 5 triangle.

1. Get each student to draw a triangle with sides 3cm, 4cm, and 5cm.

2. Give each student three 3cm cuisenaire rods and four 4cm cuisenaire rods.  Get them to lay out the rods so that they make a square on each of the two shorter sides.

3. Now move the rods to make a square on the hypotenuse.  This square uses the same rods to make it as the two smaller squares so it must have the same area.

4. Check by using algebra 3²+4²=9+16
                                              =25
                                              =5²

5. Discuss whether this proves that the theorem is true (No).  Why or why not? (It only provides an example, we now know it is true for a triangle with sides of 3cm, 4cm, and 5cm).  Can we use this method to prove the theorem is true? (No).  Why or why not? (It will only work effectively with natural numbers, and Pythagoras’ Theorem is true for all right-angled triangles).

6. Discuss Pythagorean triples.  Challenge students to find another triple where a, b and c are less than 100.

Session 2

In this session we explore of proofs of Pythagoras’ Theorem.  Depending on your class you might want to use all, some, one or none of these proofs.  They could be used in a workstation approach, as a series of teacher directed explorations, or as a demonstration to the class.

1. There have been many proofs of Pythagoras’ Theorem (there are 38 at http://www.cut-the-knot.org/pythagoras/) but one of the clearest and easiest to understand is the one used by Pythagoras himself.  The proof can be presented as purely diagrammatic, or the algebra can be included.

1. Draw the diagram, label all the sides of triangles and squares as a, b, or c, and colour as shown (or use Copymaster 1). 

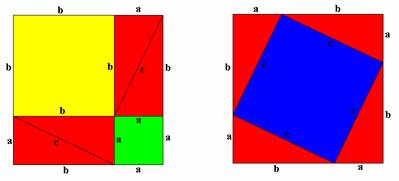
2. Ask students to see if they can explain how the diagram proves Pythagoras’ Theorem.  Discuss suggestions.
3. Ask students what the area of the two big squares is (the ones made up of triangles and squares). (They are both the same size, (a+b) x (a+b) ).  Does this help prove the theorem?
4. If we removed the four red triangles from each diagram, what would be the area of what is left of each big square?  (For the first square (bxb)+(axa), or a²+b², and for the second square cxc, or c²).  Since the two squares started out the same size and had the same amount taken off them a²+b² must equal c².
5. For the full algebraic proof, start with the area of each large square, and break it down into the individual shapes.

1. The first square: (a+b)² = a²+b²+4(½ ab) This is worked out by adding the green square, plus the yellow square, plus four red triangles each with area of half base times height (½ ab).
2. The second square: (a+b)² = c²+4(½ ab)  This is worked out by adding the blue square, plus four red triangles each with area of half base times height (½ ab).
3. Since (a+b)² = (a+b)² , we can state a²+b²+4(½ ab) = c²+4(½ ab).
4. By subtracting 4(½ ab) from each side we are left with a²+b² = c²

    

2. For a cut and paste proof, use Copymaster 2.  

1. Colour the three squares so that the pieces can be identified.
2. Cut out along all the lines and rearrange as shown below.

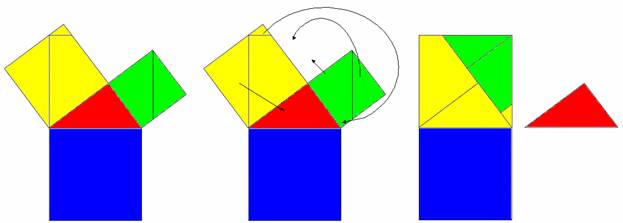
3. Clearly the size of the top (green and yellow) square is the same as that of the bottom (blue) square, and since the top square represents the sum of the squares of the two smaller sides and the bottom square represents the square of the hypotenuse the theory is proven.

3. Another diagrammatic proof  (Copymaster 3)

1. Start with the right-angled triangle, and a square drawn on each side. 
2. Colour the two smaller squares one colour and the larger square a different colour.  Pythagoras’ theorem states that these two areas are the same.
3. Now colour three triangles the same size as the original one each of the two colours (as illustrated).
4. This makes two irregular, but identical, pentagons that clearly have the same area.
5. If the two pentagons have the same area, then the two smaller squares must have the same area as the larger one.

    

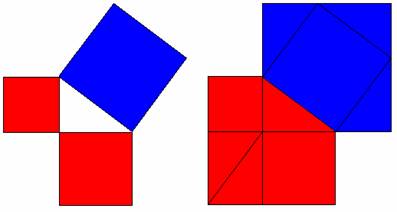
4. An interesting class discussion could be based around the question “Which of these proofs is the best?”  (There is no right answer, they all have strengths and weaknesses).

Session 3

Using Pythagoras’ Theorem to find the hypotenuse of right-angled triangles.

1. Ask the class Now that we know Pythagoras’ Theorem is true, how can we use it?
2. Draw a right-angled triangle on the board and label the two shorter sides with the numbers 5 and 8.
3. Ask the class for suggestions how they could work out the length of the side that is not labelled.
4. Work through the example with the class (working for this example is show at the top of Copyamster 4)
5. Give out a copy of Copymaster 4 to each student.  Those that are confident can work independently, those that are unsure could be guided through another example.
6. Early finishers could be challenged to set each other further problems.

Session 4

Using Pythagoras’ Theorem to find side lengths other than the hypotenuse.

1. Ask the class How can we use Pythagoras’ Theorem to work out a side length other than the hypotenuse?
2. Draw a right-angled triangle on the board and label one of the shorter sides 6 and the hypotenuse 9.
3. Ask the class for suggestions how they could work out the length of the side that is not labelled.
4. Work through the example with the class (working for this example is show at the top of Copymaster 5)
5. Give out a copy of Copymaster 5 to each student.  Those that are confident can work independently, those that are unsure could be guided through another example.
6. Early finishers could be challenged to set each other further problems.

Session 5

In this concluding session we work on applications of Pythagoras’ Theorem.

1. Review with the class Pythagoras’ Theorem. Ask for volunteers to explain their understanding of the Theorem.
2. Ask if anyone can suggest a real life example where it might be useful.
3. Work through one or two examples on the board with the class. Ensure that you emphasise the importance of drawing and labelling a diagram, to ensure that you know where the right angle is and which side is the hypotenuse.
4. Give out a copy of Copymaster 6 to each student: Those that are confident can work independently, those that are unsure could either be guided through another example or work in pairs.
5. Early finishers could be challenged to set each other further problems.
6. Leave time at the end of the class to share solutions to the problems.