This unit explores situations that involve multiplication and division using equal sets and rates. Students learn to apply the properties of whole numbers under multiplication, to derive new answers for basic multiplication and division facts.
- Derive from basic multiplication facts to solve multiplication problems with equal sets and rates.
- Identify the factors and products in equations and explain the meaning of x and =.
- Apply multiplication to find the answers to division problems.
- Learn the basic multiplication facts.
The simplest form of multiplication problem involves finding the total of a given number of equal sets. Consider this problem:
There are eight cartons of eggs. Each carton contains four eggs.
How many eggs are there altogether?
The problem can be represented mathematically as 8 x 4 = □. Eight represents the number of sets (the multiplier). Four is the number in each set (multiplicand) and represents the unit rate of “four eggs per carton.” The x symbol represents “of” in the sense of connecting eight sets of four. The empty box is the product or total and the equals sign represents sameness of quantity or balance.
Division with equal sets takes two forms depending on which factor is unknown. Sharing division comes for equally distributing a total number of objects, the dividend, into a given number shares (the divisor), which results in an amount per share (the quotient). For example:
There are 32 eggs and eight cartons of the same size.
How many eggs go into each container?
Note that 32 ÷ 8 = 4 represents the sharing of 32 (the dividend) into 8 equal sets (the divisor) which results in a quotient of “4 eggs per carton.” Division also applies to measurement contexts such as:
There are 32 eggs. Four eggs go into each carton.
How many cartons are needed?
Note that the rate is known, “4 eggs per carton”, and that becomes the unit of measure. “How many fours are in 32?” answers the problem. That can be written as 32 ÷ 4 = 8.
Both equal sharing and measuring problems are common in the real world. Developmentally, students tend to build up solutions to these problems using addition at first, progressing to multiplication. With appropriate opportunities to learn, students later come to treat division as a separate but related operation to multiplication.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- providing physical materials so that students can anticipate actions and justify their solutions. Use materials like cubes and counters, and suitable collection vessels, such as clear plastic glasses, to model situations and connect strategies used by the students to the quantities that are represented
- connecting symbols and mathematical vocabulary, especially the symbols for multiplication and division (x, ÷) and for equality (=). Explicitly model the correct use of equations and algorithms and discuss the meaning of the symbols in context
- altering the complexity of the numbers that are used. Multiplication with factors such as two, four, five, ten, and division with the same divisors, tend to be easier than factors such as three, six, seven, eight and nine
- varying the size and place value structure of the multiplicands to make problems more accessible, e.g. 4 x 15 is easier than 4 x 14 or 4 x 17. A similar classification is true for the choice of dividends, e.g. 63 ÷ 3 is easier that 57 ÷ 3
- encouraging students to collaborate in small groups and to share, and justify, their ideas
- using technology, especially calculators, in predictive, pattern-based ways to estimate products and quotients, e.g. Is the answer to 57 ÷ 3 closer to ten, twenty or thirty? How do you know? Allow use of calculators where you want students to focus more on the process of getting a reasonable answer than on practising calculation skills.
The context used for this unit include sports, packaging food, playing games and gardening to provide everyday situations that students are likely to be interested in. You may wish to change the contexts to situations more relevant to your students’ everyday lives, interests, or cultural identities. For example, cookies in cartons might become kumara or corn in bins at a hāngi, sports might become kapa haka events, and gardening might be related to the local community garden. Encourage students to be creative by accepting a variety of strategies from others and asking students to create their own problems for others to solve, in contexts that are meaningful.
Te reo Māori vocabulary terms such as whakarea (multiply), tauwehe (factor), otinga (product), and whakawehe (divide, division) could be introduced in this unit and used throughout other mathematical learning.
- Slavonic Abacus or virtual version
- Calculators
- Linking cubes, counters, or other discrete objects
- Containers (Transparent plastic cups, ice-cream containers, small cardboard boxes)
- Copymaster 1
- PowerPoint 1
Session One
Begin each session in this unit with an exercise about in deriving from basic facts. Use a Slavonic Abacus to show how many different facts can be found from a given basic fact. Preferably use a physical abacus though virtual forms of the abacus are available online.
- Model the multiples of five, or another basic fact that is appropriate to the knowledge of your students. Choose one set of multiplication basic facts to focus on throughout the session. The abacus below shows 6 x 5 = 30.
- Begin with the first factor being even and relate the answers to multiples of ten.
For example:
Why are the answers to 6 x 5 and 3 x 10 the same?
Students might notice that two fives make one ten, which explains the doubling and halving effect. Otherwise, draw attention to the halving of 6, and the doubling of 5. Using proportional adjustments, such as doubling and halving or thirding and trebling, can make it easier to solve multiplication problems. - Make a sequential list of the even multiples of five (or of the other basic facts family you have chosen):
2 x 5 = 10
4 x 5 = 20
6 x 5 = 30, etc.
What does 0 x 5 equal? What does 10 x 5 equal? 12 x 5 equals? - Invite students to give facts that lie “between” the listed facts, e.g. 3 x 5 = 15 and lies between 2 x 5 and 4 x 5.
You might encourage your students to remember the products if they do not already know them. Recite the facts in order, 1 x 5 =5, 2 x 5 = 10, 3 x 5 = 15, …etc. Erase two facts randomly each time and see if your students can recall the facts. Move to calling out particular facts for them to provide the product, e.g. “Seven multiplied by five.”
Students could also be provided with whiteboards and asked to write down the facts individually or with a partner. - Start with a given fact, e.g. 6 x 5 = 30.
If we know six multiplied by five equals 30, what other facts could we work out?
Some examples might be:
5 x 5 = 25 7 x 5 = 35 6 x 4 = 24
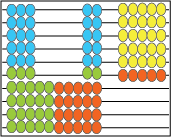

6 x 6 = 36 6 x 7 = 42 12 x 5 = 60
For each derived fact, show clearly how 6 x 5 is altered by moving beads on the abacus (as shown above).
- Give students another known fact, e.g. 8 x 5 = 40.
Tell them to create a spider’s web of facts that can be found using 8 x 5. Ask them to make as many connections as they can.
For example: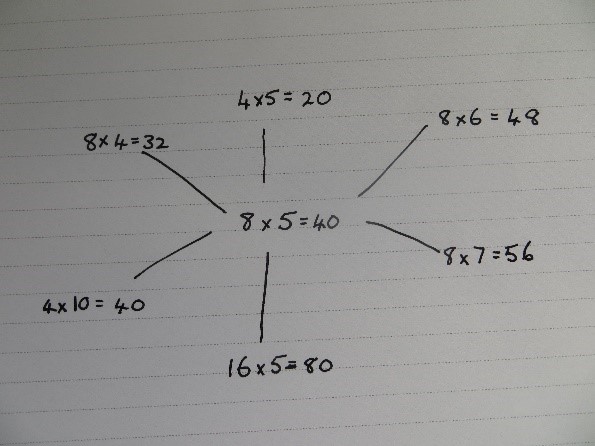
Share the students’ ideas and create a large whole class spider’s web of connections. - Move to the main investigation of the lesson (PowerPoint 1, Slide One)
Mere has 60 kumara seedlings.
She wants to space the plants out in straight rows.
How many rows can she make?
How many seedlings will go in each row? - Let your students investigate the problem in pairs. Allow access to calculators for students who need extra support. Encourage recording of their solutions.
How many different answers can you find? - Roam as your students work. Look for them to identify the problem as finding factors that multiply to a product of 60.
Can you find all the possible answers? - Gather the class after an appropriate time. Aim to create a systematic list of possible ways Mere might plant her kumaras. There is no stipulation in the problem that the same number of seedlings are in each row.
Solutions like 12 + 8 + 12 + 8 + 12 + 8 and 7 + 5 + 6 + 6 + 8 + 4 + 9 + 3 + 10 + 2 are acceptable (the addends are the number of seedlings in each row). These strategies usually have a system involved. For example, the last set of addends seems to be based on 12 (7 + 5, 6 + 6, etc.). Concentrate on solutions in which the numbers of plants in a row are equal. As students offer solutions organise your recording like this: - Ask: Are there answers ‘in between’ the solutions we have?
Students might try out three rows, four rows, seven rows etc. to see if that number of rows will work. A calculator might prove useful to find missing solutions. You could discuss simple divisibility rules, e.g. the digits of numbers divisible by three always add to a multiple of three, 54 ÷ 3 = 18 (divisible) and 5 + 4 = 9 (a multiple of three). - What operation will you key in?
Division is efficient while multiplication requires a bit of trial and error, e.g. 60 ÷ 8 = 7.5 which is preferable to 8 x 6 = 48, 8 x 7 = 56, 8 x 8 = 64,… Aim to get a full set of factors for 60. Note that each pair of factors, such as 5 x 12, gives two solutions to Mere’s problem, e.g. 5 rows of 12 plants or 12 rows of 5 plants. - Slide Two of PowerPoint 1 extends the problem:
After Mere has planted her 60 seedlings Uncle Rewa gives her 12 more.
“That works out okay,” she says, “I’ll just put more plants in each row.”
Which of the previous solutions will still work if 12 plants are added? - Let students work on the amended problem.
Do they recognise for a solution to be built on, at least one existing factor must be a factor of 12?
For example, 2 rows of 30 plants cannot be changed to “3 rows of …” but it can be changed to 2 rows of 36 plants. 5 rows of 12 plants can be changed to 6 rows of 12 plants.
Come up with a list of solutions; 1 row of 72, 2 rows of 36, …, 6 rows of 12.
Are there any ways to plant 72 kumara seedlings in equal rows that are not on our list?
Students might identify 8 rows of 9 and 9 rows of 8 but these options cannot be created from the solutions for 60 plants without transplanting. - Ask students to reflect on important words they have encountered, particularly "factor", and "product". They could write a definition for each word in their book, or you could add the class-created definition to the PowerPoint. Also ask them to take a specific equation, such as 4 x 15 = 60 and explain the meaning of the symbols x and = with a partner. Pair up students with different levels of mathematical knowledge to encourage tuakana-teina.
Session Two
- In the introduction of the lesson use the Slavonic Abacus to connect the “ _ multiplied by ten” facts to the “_ multiplied by nine” facts. For example:


6 x 10 = 60 so 6 x 9 = 54 (Six less)
- Develop a set of “nine times” facts, e.g. four times nine equals 36 (4 x 9 = 36). Look for patterns in the list of facts.
Can you find patterns in the set of nine times facts?
1 x 9 = 9
2 x 9 = 18
3 x 9 = 29
…
9 x 9 = 81
10 x 9 = 90
Students might notice these patterns:
In the products the tens digits go up by one while the ones digits go down by one.
The multiplier is always one less than the tens digit in the product, e.g. In 8 x 9 = 72, 7 is one less than 8.
The digits in the product always add to nine, e.g. 4 x 9 = 36, 3 + 6 = 9. - Encourage students to think about why the patterns happen.
- Work towards memorising the times nine facts by reciting them, creating flash cards and practising. There are many sites on the internet for practising basic facts and you can use the basic facts tool on e-ako maths as well.
- Move on to the main problem of the lesson (Slide Three of PowerPoint 1). Is worthwhile to act out the problem with the students first. Use counters, cubes, or other objects to be cookies, with different colours used for each flavour.
- Ask the students to solve the problem in small groups of two or three. It is important that they record their mathematical thinking, both to support their work and as an artefact that can be shared with other students. As you roam look for your students to:
- Recognise and honour all the conditions of the problem, e.g. all plates the same, all cookies exhausted.
- Use multiplication facts to support them trial possible compositions for the plates. Note that access to a multiplication facts chart, or calculator might be needed to give access for some students.
- Realise that common factors of 24, 36 and 48 are important to the problem.
- Work beyond a single solution to consider all the possible solutions. Note that students should decide which of possible plate compositions will be the most useful for selling at a fundraising event.
- After a suitable time, gather the class to share ideas. Discuss useful strategies and connect those strategies to important vocabulary such as factor, and multiple. Relate the action of sharing equally to division. For example:
Will eight plates work? Why? Why not?
24 ÷ 8 = 3, 36 ÷ 8 = 4 r4 or 4 ½, 48 ÷ 8 = 6. Therefore, eight plates will only work if some cookies are not used or are cut into halves. One strategy breaks a condition and the other will ruin the presentation of each plate. - Discuss: How can we find the number of plates that might work?
Two plates will work because 24, 36 and 48 divide equally by two. Each plate might be too big to sell.
Three plates will work because 24, 36 and 48 divide equally by three. Each plate might be too big to sell. Discuss:What is a good strategy to see if a certain number of plates will work?
Will five plates work?Why? Why not?
Five plates will not work as 24, 36, and 48 are not divisible by five (not in the five times table).
Will six plates work? What about seven plates? Etc.
Some students might list all the factors of 24, 36, and 48 to see what numbers of plates might work. You might give the students the start of the table and ask them to complete it.Number of Plates 1 2 3 4 5 6 7 8 9 10 11 12 24 raisin ● ● ● ● ● ● ● 48 oatmeal ● ● ● ● ● ● ● 36 chocolate ● ● ● ● ● ● ● - Discuss: Should we stop at 12 plates? Are there other numbers of plates that might work?
If we use six plates, how many of each cookie is on each plate?
If we use twelve plates, how many of each cookie is on each plate?
Can we work this out from the six plate answer? How? - Make a collective decision about the best answer, given the context.
Six plates with 4 raisin, 8 oatmeal, and 6 chocolate cookies is probably the most practical. - You might vary the cookie problem by changing the numbers. For example, 25 raisin cookies, 35 oatmeal cookies, and 45 chocolate cookies.
- Introduce the hiking and cycling problem on Slide Four of PowerPoint 1. Act out what is meant by rates of 3 kilometres per hour and 7 kilometres per hour. Students will be familiar with cars travelling at 100 or 50 kilometres per hour. Use car travel as a helpful context.
- Let students attempt the problem individually or in small groups. Roam the room and look for:
- Do they use the rate as the unit of measurement? For example, the walking time can be calculated by 25 ÷ 3 = 8 r1 or 8 1/3 hours.
- Do they see similarities between the cookie problem and the walking/hiking problem?
- Gather the class and discuss solution strategies. You might use a double number line to organise the information in the problem.
A double number line of Nico’s hike looks like this:
- Build up the first few time and distance pairs, (1,3), (2,6), (3,9),...
Is there an easier way to predict the amount of time Nico will take?
Students might see that multiplying the time, in hours, by three gives the distance that Nico hikes, in kilometres. 8 x 3 =24 so it takes Nico over eight hours. Some students might be able to get more precise.
If Nico hikes 3 kilometres each hour,how long will it take him to hike 1 kilometre? (1/3 of an hour or 20 minutes) - A double number line for Kat’s cycle looks like this:

Build up the time and distance pairs in a similar way, (1,7), (2,14), (3,21),... Can students see that multiplying the time, in hours, by seven gives the distance, in kilometres?
Can they be more precise than saying that “Kat takes over 8 hours to cycle 48 kilometres”? (two kilometres takes her 2/7 of an hour. That’s less than one third and equals about 17 minutes.) - You might change the conditions of the Nico and Kat problem to make it easier or harder, and to see if students have generalised how to solve simple rate problems. For example:
Niko is hiking a 30 kilometre track.
He can walk at about 4 kilometres per hour, including rest stops.
Kat is cycling a 45 kilometre trail .
She rides at about 6 kilometres per hour, including rest stops.
Session Three
- The introduction of this lesson involves repeated doubling to connect multiplying by two, four and eight. Start simply with 2 x 3 then 4 x 3 then 8 x 3.


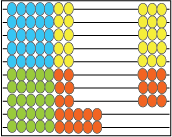
2 x 3 = 6 4 x 3 = 12 8 x 3 = 24
What patterns can you see?
Students should notice that the product doubles as the multiplier doubles.
What multiplication fact would come next?
(16 x 3 = 48. You might need two abacuses to show that)
- Introduce another example such as 2 x 6 (six multiplied by two) then 4 x 6 then 8 x 6. Ask students to find the total number of beads each time:



2 x 6 =12 4 x 6 = 24 8 x 6 = 48
What patterns can you see?
- Give students some examples to solve without the abacus model. For example:
2 x 4 = 8, so 4 x 4 = ____, so 8 x 4 = ____, so 16 x 4 = ____
2 x 8 = ____, so 4 x 8 = ____, so 8 x 8 = ____, so 16 x 8 =
7 x 2 = ____, so 7 x 4 = ____, so 7 x 8 = ____, so 7 x 16 =
2 x 11 = ____, so 4 x 11 = ____, so 8 x 11 = ____, so 16 x 11 = - Introduce the game Dicey Times to your students using slides 5 and 6 for PowerPoint 1. The aim of the game is to place the dice numbers in the circles to maximise the score. The points for each circle come from how many of the numbers in a row, diagonal or column are multiples of the dice number.
- Copymaster 1 provides the grid shown in PowerPoint 1 and another simpler set on the first page. The second page provides blank grids for you to enter new numbers or for the students to create their own grid.
Note that a simplified form of the game is available using this Figure It Out task: Dicey Dabble. - As students play the game a few times look to see that they:
- Recognise that strategic choice about where to locate the dice number improves their chance of winning.
- Scanning each row, column and diagonal for common multiples helps locate the best spot for a given dice number.
- Notice that a dice number of 1 gives 4 points whichever row, column or diagonal it is located on.
- Some numbers, like 17 and 23, are multiples of only one. They are prime numbers. Locating a dice number of 1 is the only way to get points from these numbers in the grid.
- Gather the class and use slide seven of PowerPoint 1 to play a virtual game together. Discuss the best circle to locate each dice numbers and why that circle is best. Try to bring out the teaching points above.
Session Four
- Begin the session with deriving the “multiplied by six” and “multiplied by seven” facts from the “multiplied by five” facts. The pattern involves the distributive property of whole numbers under multiplication.
Use this example first: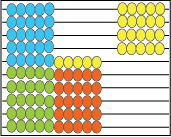

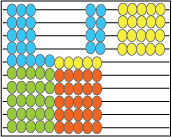
4 x 5 = 20 4 x 6 = 4 x 7 =
- Use 8 x 5 next:
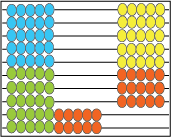
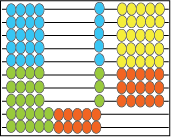

8 x 5 = 40 8 x 6 = 8 x 7 =
- Provide students with three different “multiplied by five” facts and ask them to draw a spider web of related facts. For example, the web for 6 x 5 = 30 might have arms of 6 x 6 = 36, 6 x 7 = 42, 6 x 4 = 24, 3 x 10 = 30, 6 x 50 = 300, 6 x 8 = 48, 5 x 6 = 30, etc.
- After students create their webs, pair them with another student to compare their facts.
Can you make your spider web even larger? - Use Slide 7 of PowerPoint 1 to discuss four different sports. You may need to hunt for short clips online if students are not familiar with how the games are played.
Suppose we decide to run a sports day.
Each sport is on at a particular time of the day.
No other sport is played at that time. It is too hard to organise.
We want as few players as possible that are reserves at any time. Everyone must be in a team.
What is the ideal number of entries (people) for the sports day?
Explain your answer. - Let your students work in small teams to solve the problem. Encourage them to record their thinking so they can explain their solution to the whole class.
- Roam the room as teams work looking for the following:
- Use of multiples to find the best numbers of players for each sport.
- Scanning for common multiples to find a number of players that works well for many sports.
- Recognition that multiples of 4 are in multiples of 8, and multiples of 5 are in multiples of 10.
- The last point simplifies the problem a lot as students need to find a number of players that is a multiple of 8 and 10. The smallest number that fits is 40 players though students may suggest numbers like 80 that also work. In fact, any multiple of 40 will work.
- Gather the class to discuss students’ strategies, highlighting the points above. Introduce Slide 8 to add more complexity. All the sports on Slide Seven are still being played but introduce Petanque (3 players per team), Volleyball (6 players per team), and Softball (9 players per team).
How many players will we need at the Sports Day if we include these sports as well?
This task is very challenging but students will have some idea of how to approach it from the earlier problem. Make calculators available as the focus is on thinking with multiples, not on calculation. - Let students work in small teams again. Roam to room and look for students to:
- Recognise the need for common multiples.
- Recognise that the number of players must be a multiple of 40 (from the previous sports).
- Realise that numbers of players for softball (multiples of 9) will also work for Petanque (multiples of 3). Even multiples of 9 also are multiples of 6.
The easiest solution is to multiply 40 by nine. 360 is divisible by 8, 10 and 9, which is required for there to be no reserves at any time.
Session Five
- Use the final session as an opportunity for students to demonstrate their growing multiplicative thinking. Ask them to choose from the following tasks from the Figure It Out series.
- The Hundreds Board Hunt from Multiplicative Thinking, Level 3.
- Multiples and Factors, from Multiplicative Thinking, Level 3.
- Fun Rides, from Number, Level 3.
- Busking Blues, from Number, Level 3
- , Book Two.
- That Old?, from Number, Level 3, B
- , Book Three. Easy Nines, from Number, Level 3, Book Three.
- Movie Maths, from Number, Level 3ook Two.
- Use the opportunity to roam the room and assess students’ achievement of the learning outcomes.
Dear parents and whānau,
In mathematics this week, our focus has been on multiplication and division. We learned to work out new multiplication facts from facts we already know. To show how that works, ask your student which facts could be worked out from 8 x 5 = 40.
He or she might say that 8 x 5 and 4 x 10 have the same answer. They might say that 8 x 7 must be 16 more than 40 and explain why. There are lots of other connected facts.
Now is a good time for your student to practice their basic multiplication facts at home and school. You might like to find out what facts they know and help them to learn the facts they do not.