In this unit we use rectangular models or arrays to explore numbers from one to fifty. We systematically identify all the factors of numbers, and are introduced to prime numbers.
- Model the numbers from 1 to 100 as rectangular arrays.
- Connect the possible arrays for a given number to the factors of that number.
- Identify the factors of the numbers 1 to 100 using divisibility.
- Identify whether natural numbers from 1 to 100 are prime, composite, or a special case (i.e. 1).
- Calculate square roots using calculators and array models.
This unit looks at the number concepts of factors, multiples, and prime numbers. These fundamental ideas have a surprisingly wide range of applications. Searching for certain types of prime number has become a test for the speed of new computers and methods of protection of computers for unwanted access. Prime numbers are an integral part of modern coding theory. This allows the easy encryption of words and numbers but means that decoding is quite difficult. Codes are based around the fact that the prime factors of large numbers are hard to find. Such codes are used by banks and the military because they are very difficult to break, even in the age of computers.
Finding factors of a given number can always be done by a systematic search. A search for prime numbers firstly assumes that we are looking only at natural numbers {1, 2, 3, 4, 5, …} That means zero cannot be prime. Starting at 1, each consecutive number is tested to see if it is a factor of the number in question. The search for factors from above and below continues until they converge on the square root of the number. For example, to find the factors of 18, first check 1, then 2, then 3, then 4, and so on until 5, since five is just greater than the square root of 18 (√18 = 4.24, 2dp.). That way all the factors of 18, or any other number for that matter can be found. Systematic searches are important throughout mathematics, especially to verify that all possible answers have been found.
The convergence of factors from above and below to the square root works in this way. We need not test any numbers above 4.24. This is because any number above 4 will be paired with a factor less than 4 and all the smaller potential factors were tested. For 18 this means that we get 1 and 18 by testing for 1; 2 and 9 by testing for 2; 3 and 6 by testing for 3. Four is not a factor of 18 so the job is done.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- altering the degree of abstraction from working with cubes, to making diagrams of arrays, to working with only numbers.
- altering the size of the numbers that students find factors for. Generally, larger natural numbers are more difficult to work with.
- organising pairs and small groups of students to be comprised of students with mixed levels of mathematical knowledge and confidence to encourage tuakana-teina (peer learning)
- providing opportunities for students to explain and justify their thinking with the use of materials and diagrams
- providing calculators so students can test for divisibility if their basic facts knowledge and multiplicative thinking is not strong.
The context for this unit is about using cubes to create arrays. The context can be connected to everyday life through situations where arrays are useful. For example:
- Creating an array of kumara pits.
- Looking at arrays on gameboards, like Chess and Twister.
- Designing parking lots for cars.
- Setting out a group formation in dance, kapa haka or waka.
Te reo Māori kupu such as tūtohi tukutuku (array), tau toitū (prime number), tauwehe (factor), whakarea (multiply, multiplication), and whakawehe (divide, division) could be introduced in this unit and used throughout other mathematical learning
- Cubes
- Calculators
- A3 sheets of paper
- Hundreds boards (Material Master 4-4)
Getting Started
In this session students investigate the possible rectangular arrays for given whole numbers. They record the appropriate factors for each array.
- Give each student 12 cubes and ask them to form a rectangle using all 12 cubes.
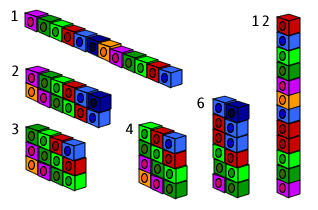
What size is the rectangle you have made? (Discuss the description of rectangles using rows and columns.)
Have we found all the rectangles? How do you know? (Expect the students to check each of the numbers to 12 although some may realise that you only need to check until the factors start repeating, e.g. 3 x 4 and 4 x 3. Highlight that the factor pairs repeat after 3 (Square root of 12 = 3.46). - As a class record each of the rectangles using squared paper.
- Attach these rectangles to an A3 page headed with a 12. Record the expression with each rectangle. Organise the rectangles from 1x12 to 12x1. (This will allow for more systematic comparison with the factors of other numbers.)
Are each of the rectangles unique? (‘Unique’ means unlike any others such as one array cannot be rotated or reflected to make another)
If we remove any rectangles that are copies, how many unique rectangles are there? (1 x 12, 2 x 6, 3 x 4).
What name do we give to numbers that multiply like 3 and 4, to give a number, like 12? (Factors of 12)
You might record the findings using formal notation:
Factors of 12 = {1, 2, 3, 4, 6, 12}
It is also interesting to consider why whole number are not factors of 12. For example, 5 is not a factor because all factors of 5 end in either 0 or 5 (in the ones place). - Give each pair of students a number in the range 10 to 24) and ask them to form as many unique rectangles as they can using that number of cubes. As they form the rectangles, first with cubes and then on squared paper, ask questions to draw their attention to the factors of the number in a systematic way, such as arranging the first factor from lowest to highest.
How many rectangles have you found for your number?
How do you know you have found them all?
Why do some numbers have more rectangles than others?
Are there any numbers that form only one rectangle?
Is it possible to predict these ‘one rectangle’ numbers? - Ask each pair of students to glue their paper rectangles to the ‘page’ for their number. Alongside each rectangle, a corresponding multiplication should be written.
For example, 4 x 3 or 3 x 4 for this array:
- Share the number pages as a class.
Which number has the most rectangles? (24) Why? Students may think that 24 has the most factors because it is the largest number. You might investigate 25 that has only 3 factors.
Which numbers have only one rectangle (two factors)? (The primes 11, 13, 17, 19, 23)
Which numbers have only 2 rectangles (four factors)? (4, 6, 8, 9, 10, 14)
Can a number have 3 rectangles (six factors)? (Yes, 12 does)
Can a number have 4 rectangles (eight factors)? (Yes, 24 does)
Note that students may not recognise squares as a special class of rectangles. For example, they may not include 4 x 4 in their search for arrays with 16 cubes. It is important to discuss this point as it has implications for geometry as well. - Formally list sets of factors, e.g. Factors of 10 = {1, 2, 5, 10} and Factors of 11 = {1,11}.
What happens when one of the rectangles is a square?
These numbers are known as square numbers and they have an odd number of factors, e.g. Factors of 9 = {1, 3, 9}.
Numbers that have more than two factors are called composite numbers. What numbers in the range 10-24 are composite? (10, 12, 14, 15, 16, 18, 20, 21, 22, 24)
Numbers that have only two factors are called prime numbers. What numbers in the range 10-24 are prime? (11, 13, 17, 19, 23)
Can a number be neither (not) composite or prime? (Usually this is an ‘either or’ choice except for the special case of one)
How many rectangles can be made with one square? (only a 1 x 1 rectangle is possible, so 1 is a special case, neither composite or prime but it is a square number.) - Add these key points to a class chart, or ask your student pairs to create a one-page display that demonstrates and explains what factors are, giving examples of one square number, one composite number, one prime number, and one number that is not a composite or prime (1). They should use cube drawings and written equations to explain these key points. Roam and support students to understand each of these key concepts as necessary.
Sessions Two, Three and Four
Over the next 2-3 days ask your students to create rectangle charts for each of the numbers from 1 to 100. Use the charts to develop their understanding of factors, multiples, and primes.
- Look at the charts from the previous day.
I could say that the factors of 12 are 1, 2, 3, 4, 6 and 12. What does the word factor mean?
You might look up the internet to create a formal definition of the word “factor.”
I could say that 12 is a multiple of 1, 2, 3, 4, 6, and 12. What does the word multiple mean? Create a formal definition of the word “multiple.” - Choose other numbers in the range 10-24 and invite your students to make statements that use the words factor/s and multiple/s. The characteristics of multiples of a given number are used to test for divisibility by that number. For example, multiples of 2 are {2, 4, 6, 8, 10, 12,…} so to test to see if a number has 2 as a factor we only need to check that it is even, so has 0, 2, 4, 6 or 8 in the ones place. The divisibility rule for 5 is also easy but for other factors like 3, 6, and 9 the rules involve digital sums.
- Put the numbers from 24 to 100 in a hat or special container. One student in the pair picks a number from the hat and then the two students work together to construct all rectangular arrays for the number. They should record the rectangles on squared paper and then attach these rectangles to an A3 piece of paper. As the students work ask questions that focus on their identification of the factors of a number.
How many rectangles have you found for your number?
How do you know you have found them all?
What are the factors of your number?
Is your number prime or composite? How do you know?
Is your number a square number? - An interesting investigation is the relationship between square numbers and the square root function. For example, 64 is a square number since 8 x 8 is one possible array. The factors of 64 are {1, 2, 4, 8, 16, 32, 64}. An odd number of factors is one property of natural numbers that are squares. Show students that a calculator can be used to find that the square root of 64 is 8.
What does 8 as a factor have to do with an array of 64 cubes? (8 is the side length of a square with an area of 64 square units.)
Using this knowledge, students could add the square root of their number (if it is a square number) to their chart. Ensure they use the correct notation and can explain the connection between the square root and their display of squares. - When the students have completed a number, they select another from the hat.
- Roam ans support students to create their charts as needed. At the end of each session look at the developing display of rectangle charts. Invite pairs of students to share their findings with the class.
- You might use a hundred chart to colour code the composite and prime numbers. Provide students with their own chart and show a virtual hundreds board on a large screen. This may lead to a discussion about which kind of number is most common. Students may notice that primes become less frequent as the range is extended.
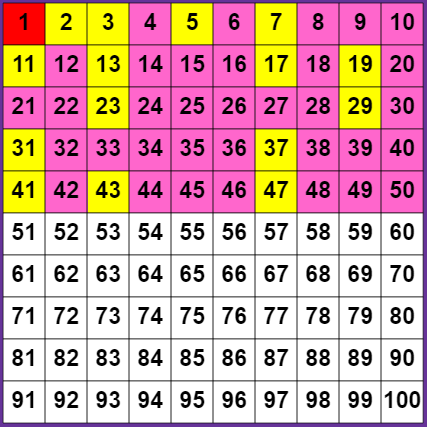
- Note that primes tend to be located next to multiples of six. For example, both 5 and 7 are primes. However, being one more or less than a multiple of six does not guarantee that a number is prime. For example, 48 is a multiple of six. 47 is prime but 49 is a square composite.
Session Five
Today we look at our completed display of rectangle charts and create a newsletter for our families telling them about our findings.
- Display the factor charts, in order, for the class to examine.
- Encourage the students to look at the charts and write statements (in pairs) about their observations. The following questions may be used as prompts for the students.
Which number has the most factors?
How many prime numbers are there less than 100?
Is there a way to predict if a number, like 51 or 57, is prime?
What number do you think is the most interesting? Why?
Which decade has the most prime numbers? Why do you think it is the tens decade? - Share statements.
- Investigate the method used by a mathematician from ancient Greece. His name was Eratosthenes, and he is most famous for estimating the circumference of the Earth. That was quite a feat for a person who lived from 276 - 194BC. Eratosthenes used a sieve method to leave behind only the primes. You can find videos online explaining the method. Your students might be interested.
- Use students’ statements to form the basis for the newsletter home.
- In addition to the class statements you may like to include the following challenging brainteaser.
Challenge: The Census Problem
A census taker approaches a house and asks the person who answers the door.
"How many children do you have, and what are their ages?"
Person: I have three children. The product of their ages is 36, the sum of their ages is equal to the address of the house next door."
The census taker walks next door, comes back and says to the woman.
"I need more information."
Person: "I have to go. My oldest child is sleeping upstairs."
Census taker: "Thank you, I have everything I need."
Question: What are the ages of each of the three children?
This is a very famous problem and the first reaction of people is often that insufficient information is given. However, it can be solved.
First make a systematic is of the sets of three factors that have a product of 36, since the ages of the three children have a product of 36. Begin with one as a factor and increase the size of factors from there:
1 x 1 x 36 (unlikely a child is 36 years old)
1 x 2 x 18, 1 x 3 x 12, 1 x 4 x 9, 1 x 6 x 6
2 x 2 x 9, 2 x 3 x 6,
3 x 3 x 4
Since the only combination possible with four is covered that is the end of the list. Next find the sums by adding the factors.
1 + 1 + 36 = 38,
1 + 2 + 18 = 21, 1 + 3 + 12 = 16, 1 + 4 + 9 = 14, 1 + 6 + 6 = 13,
2 + 2 + 9 = 13, 2 + 3 + 6 = 11,
3 + 3 + 4 = 10.
The only way the census worker needs more information is the possibility that two or more sets of factors might have the same sum. In this case 1, 6, and 6 have the same sum and 2, 2, and 9.
Knowing that there is an oldest child means that 2, 2, and 9 are the ages of the children.
Dear family and whānau
This week at school we have been investigating prime numbers, factors, composite numbers, and square roots. Ask your child to tell you what they have found out.
We are also working on a brainteaser. See if your family can work it out together: if you need, the answer is given below the problem.
Census Problem
A census taker approaches a house and asks the woman who answers the door.
"How many children do you have, and what are their ages?"
Woman: I have three children. The product of their ages is 36, the sum of their ages is equal to the address of the house next door."
The census taker walks next door, comes back and says to the woman.
"I need more information."
Woman: "I have to go. My oldest child is sleeping upstairs."
Census taker: "Thank you, I have everything I need."
Question: What are the ages of the each of the three children?
Solution to brainteaser
For a start we have to find all of the sets of three numbers whose product is 36. These can be found systematically. We do this below but we also find the sum of the factors as this is part of the problem.
| Three factors | Sum of factors |
| 1 x 1 x 36 | 38 |
| 1 x 2 x 18 | 21 |
| 1 x 3 x 12 | 16 |
| 1 x 4 x 9 | 14 |
| 1 x 6 x 6 | 13 |
| 2 x 2 x 9 | 13 |
| 2 x 3 x 6 | 11 |
| 3 x 3 x 4 | 10 |
From the table the census taker would have known the ages of the children if the number of next door was anything but 13. But they still needed some more information so the number had to be 13.
When the woman said that she had an eldest child then the ages had to be 2, 2 and 9 (rather than 1, 6 and 6). So that’s how the census taker worked out the ages of the children.