This problem solving activity has a geometry focus.
Poppy is trying to find a method that might enable her to find the position of her helicopter inside a rectangular region.
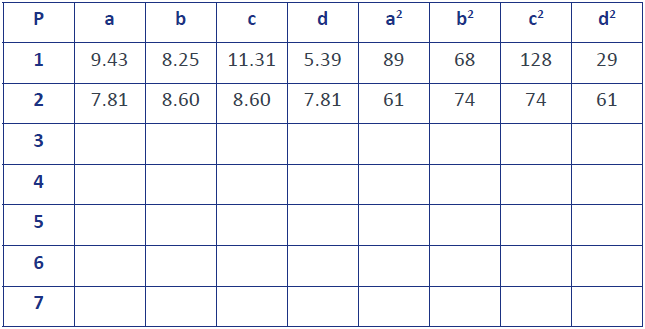
She first experimented by drawing a 10cm by 13cm rectangle and measured a, b, c and d for various points P inside the rectangle.
She started the table below.
Complete the table and try to find a relationship between a, b, c and d.
Can you justify this relationship?
- Find connections between numbers in a table.
- Use Pythagoras’ theorem in a general algebraic form.
- Measure accurately from a scale drawing.
- devise and use problem solving strategies to explore situations mathematically (be systematic, draw a diagram).
This problem has at least three aspects that are worth thinking about. First it gives the students a chance to construct and measure certain geometrical objects. Second it enables them to find a pattern in a geometrical situation. Third it gives them practice in constructing proofs using a well known result. The extension to this problem also provides the opportunity to look for a generalisation of the problem.
Looking for patterns is a key part of mathematics and mathematicians look for them in all possible situations. Knowing that this is important and practising this skill will provide a good basis for all future mathematics.
Note: The software programmes Geometer's Sketchpad or Cabri Geometry, will enable students to generate a lot of examples quickly. This will be less tedious (and more accurate) than choosing the point P and measuring a, b, c and d.
If you don't have access to either of these, the generation of the table can be accomplished more efficiently by sharing group measurements.
- Copymaster of the problem (Māori)
- Copymaster of the problem (English)
- String and measuring tools (to physically act out the problem)
- An appropriate software programme, e.g. Geometer's Sketchpad or Cabri Geometry (optional)
The Problem
Poppy is trying to find a method that might enable her to find the position of her helicopter inside a rectangular region.
She first experimented by drawing a 10cm by 13 cm rectangle and measured a, b, c and d for various points P inside the rectangle. She started the table below.
Complete the table and try to find a relationship between a, b, c and d.
Can you justify this relationship?
Teaching Sequence
- This problem could be introduced by physically acting it out with string. Four students form the corners of the region and another is the helicopter. As the helicopter person moves to various positions the students are asked to comment on the changing connections they notice between a, b, c, and d. Measurements of the string could also be taken.
- Discuss the geometric information that could be used to allow Poppy to easily find her position inside the region.
What shapes are we making here?
As d increases what happens to a? b? c? always?
Why have the squares have been included in the table? - Let the students complete the table using the class measurements and measurements made from their scale drawing.
- Encourage the students to investigate the connection between the numbers.
- Once the relationship a2 + b2 = c2 + d 2 has been found ask the students to prove this. Focus questions for those students who need extra assistance with this include:
What do we know that uses squares?
What does this relate to?
Where are the right-angled triangles in this problem?
How can we set this up? - Share student solutions.
- Student solutions will probably provide a good starting point for you to share with students a more formal proof of Pythagoras than they have seen before.
Extension
What if Poppy’s helicopter is outside of the rectangular boundary? Does the relationship above still hold?
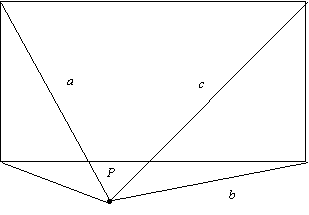
Solution
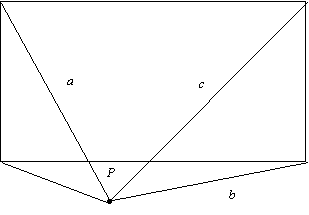
The relationship can be established by using Pythagoras’ Theorem. From the diagram above
a2 = u2 + v2 c2 = u2 + w2
b2 = x2 + w2 d2 = v2 + x2
So, a2 + b2 = (u2 + v2) + (x2 + w2)
= u2 + x2 + v2 + w2
= c2 + d2.
Solution to the Extension
Surprisingly, the same relations holds.
Again, by Pythagoras,
a2 = (x + z)2 + v2, b2 = w2 + z2
c2 = w2 + (x + z)2 and d2 = y2 + z2
a2 + b2 = (x + z)2 + y2 + w2 + z2
= w2 + (x + z)2 + y2 + z2
= c2 + d2.