Polygonal Strings
This is a problem from the number and algebra strand.
Determine the maximum area of a regular polygon with a given perimeter
Appreciate the concept of limit as it applies to the area of regular n-gons and circle that both have the same perimeter
To be able to do this problem students need to be able to calculate areas of triangles using the formula: area = ½ base length x height. They should probably have tried Peter’s Third String, Level 6 and seen how to use algebraic equations to solve problems.
Apparently in some areas of New Guinea they measure the area of land by its perimeter. When you think about it this isn’t such a good idea. A piece of land can have a relatively large perimeter and only a small area. This sequence of problems is built up from this simple bad idea.
Seven problems have been spawned by the perimeter-area tangle. These come in two waves. First there is the string of Peter’s String problems. These are Peters’ String Measurement, Level 4, Peters’ Second String, Measurement, Level 5, Peters’ Third String, Algebra, Level 6, and The Old Chicken Run Problem Algebra, Level 6 and the Polygonal String Problem, Algebra, Level 6. These follow through on the non-link between rectangles’ areas and perimeters, going as far as showing that among all quadrilaterals with a fixed perimeter, the square has the largest area. In the second last of these five problems we are able to use an idea that has been developed to look at the old problem of maximising the area of a chicken run. This is often given as an early application of calculus but doesn’t need more than an elementary knowledge of parabolas. The final problem looks at the areas of regular polygons with a fixed perimeter. We show that they are ‘bounded above’ by the circle with the same perimeter.
The second string of lessons looks at the problem from the other side: does area have anything to say about perimeter? This leads to questions about the maximum and minimum perimeters for a given area. The lessons here are Karen’s Tiles, Measurement, Level 5 and Karen’s Second Tiles, Algebra, Level 6.
Mathematics is more than doing calculations or following routine instructions. Thinking and creating are at the heart of the subject. Though there are some problems that have a set procedure or a formula that can be used to solve them, most worthwhile problems require the use of known mathematics (but not necessarily formulae) in a novel way.
Throughout this web site we are hoping to motivate students to think about what they are doing and see connections between various aspects of what they are doing. The mathematical question asked here is what can we say about the areas of various figures all of which have the same fixed perimeter? This question is typical of a lot of mathematical ones that attempt to maximise quantities with given restrictions. There are obvious benefits for this type of maximising activity.
The Extension Problem here introduces the idea of limit and so is useful as background to, or as an introduction to, the gradient of a curve. The idea of gradient and its many applications, occupies a prominent place in calculus at Levels 7 and 8.
The ideas in this sequence of problems further help to develop the student’s concept of mathematics, the thought structure underlying the subject, and the way the subject develops. We start off with a piece of string and use this to realise that there is no direct relation between the perimeter of a rectangle and its area. This leads us to thinking about what areas are possible. A natural consequence of this is to try to find the largest and smallest areas that a given perimeter can encompass. We end up solving both these problems. The largest area comes from a square and the smallest area is as small as we like to make it.
Some of the techniques we have used to produce the largest area are then applied in a completely different situation – the chicken run. This positive offshoot of what is really a very pure piece of mathematics initially is the kind of thing that frequently happens in maths. Somehow, sanitised bits of mathematics, produced in a pure mathematician’s head, can often be applied to real situations.
The next direction that the problem takes is to turn the original question around. Don’t ask given perimeter what do we know about area; ask given area what do we know about perimeter. Again there seems to be no direct link.
But having spent time with rectangles, the obvious thing to do is to look at other shapes. We actually look at polygons and their relation with circles but there is no reason why you shouldn’t look at triangles or hexagons. Here you might ask whether you can find two triangles with the same area and perimeter or what is the triangle with given area that has maximum perimeter. We have actually avoided these last two questions because of the difficulty of the maths that would be required to solve them. However, we may have got it wrong. There may be some nice answers that are relatively easy to find. If so, please let us know.
The Problem
Peter had kept a piece of string that had been on a parcel that had come for his birthday. It was 30 cm long. He played with it and made different shapes out of it all with the same perimeter of 30 cm. Then he got stuck on polygons. He wondered which of the following polygons had the biggest area: equilateral triangle, square or regular hexagon.
His sister Veronica said that she thought he could get more area inside a circle with that perimeter but she didn’t have a good reason for saying that.
Which of these figures has the biggest area?
Teaching sequence
- Introduce the problem to the class. Get them to consider how they would approach the problem.
- Let them investigate the problem in any way that they want. However, the students will probably need to draw diagrams to help them to visualise what is happening. At some stage though they will probably have to write down equations. They may need some help at this point.
- Move round the groups as they work to check on progress. Encourage them to draw large diagrams to show clearly what is going on. Help them with the idea of breaking polygons down into triangles
- If a lot of the pairs are having problems, then you may want a class brainstorming session to help them along.
- The Extension problem has an important idea about limits that should be shared with all of the class, as it will help prepare an important idea for the calculus at Levels 7 and 8.
- Share the students’ answers. Get them to write up their work in their books. Make sure that they have carefully explained their arguments.
Extension to the problem
If Peter made any regular polygon shape with his string, what would be the maximum area he could make? Is there any hope that he could get an area that was bigger than the area of the circle with perimeter 30 cm?
Solution
We need to work out the areas of an equilateral triangle, a square, a regular hexagon and a circle, all of which have a perimeter of 30 cm.
Equilateral triangle: As the perimeter of the equilateral triangle is 30 cm, one of its sides is 10 cm.
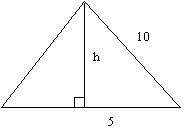
If we draw the perpendicular of the triangle, we see that, by Pythagoras’ Theorem, 102 = 52 + h2. So, h2 = 102 – 52 = 100 – 25 = 75. So h = √75. The area of the equilateral triangle is, therefore, AT = ½ x 10 x √75. This is approximately 43.30 cm2.
Square: Since the square has four sides and perimeter 30 cm, one of its sides has length 7.5 cm. So its area is AS = 7.5 x 7.5 = 56.25.
Regular hexagon: The regular hexagon has six equal sides, so each side is of length 5 cm.
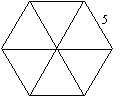
It is probably easiest to divide the hexagon into six equilateral triangles, each one of which has sidelength 5 cm. Using ideas from above, we see that the area of each of these triangles is ½ x 5 x √(52 - 2.5 2). This is approximately 10.83 cm2. So the area of the regular hexagon AH = 6 x 10.83 = 64.95.
Circle: If the perimeter of the circle is 30 cm, then we can find the radius using 30 = 2πr. So r = 30/2π = 15/2π. We’ll leave this in this form for the moment. Now the area of the circle is then AC = πr2 = π(15/π)2 = 152/π = 225/π = 71.62.
It is clear that the circle has the biggest area. It’s interesting that the areas of the regular polygons seem to increase as the number of sides increases.
Solution to the extension
Suppose that we look at a regular n-gon. In other words a regular polygon with n sides. As its perimeter is 30 cm, then one of its sides must have length 30/n and half of one of its sides must be 15/n cm long.
The diagram below shows one of the n isosceles triangles that make up the regular n-gon. Since n triangles together make up 2π at A, the angle (in degrees) in each triangle is 2π/n. So the angle BAC = 2π/n and the angle BAD is π/n.
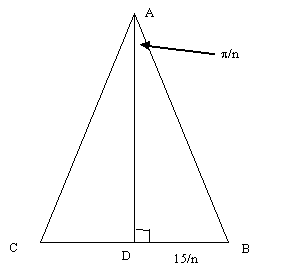
In the right angled triangle ABD, BD/AD = tan (π/n). So AD = BD/tan (π/n). And so the area of triangle ABC is BD. AD = BD2/tan (π/n) = [15/n]2/tan (π/n).
But we want the area of the regular n-gon which is formed from n triangles congruent to triangle ABC. This area is therefore AN = n{(15/n)2/tan (π/n)} = 225/[n tan(π/n)].
Let’s check to see that we haven’t made any errors here by using n = 3, 4 and 6. In these cases we should get the same values that we got for the equilateral triangle, the square and the regular hexagon.
n = 3: AN = 225/[3 tan(π/3)] = 225/3√3 = 25√3 = 43.30.
n = 4: AN = 225/[4 tan(π/4)] = 225/4 = 56.25.
n = 6: AN = 225/[6 tan(π/6)] = 225√3/6 = 75√3/2 = 64.95.
Since we do, then there is a very good chance that we have made no mistakes so far!
So AN = 225/[n tan(π/n)]. Is it obvious what value of n gives us a maximum value? You might like to program a computer to run off values for n up to say 100. It may be possible to do this if you have some calculus under your belt but that is not likely at Level 6. So you may have to rely on a table showing you that the values of AN actually keep increasing as n increases. In that case there is no biggest polygon.
Having said that though, we can show that AN is never bigger than a certain value. The thing that you need to know is that for q small, tan q is very close to being equal to q. Let’s use that approximation to see what happens.
AN = 225/[n tan(π/n)] » 225/n(π/n) since for n large, π/n is very small and so tan (p/n) is approximately equal to π/n.
Then AN » 225/n(π/n) = 225/π. Now the surprising thing is that this is the area of the circle with perimeter 30 cm!
One final thing, it runs out that tan(p/n) is always bigger than π/n. So AN is always slightly less than 225/π. We can make a regular polygon with perimeter 30 cm that is as close as we like to the area of the circle with the same perimeter but it will never quite be as big.
It at least makes sense that the area of a polygon with a large number of sides can approximate the area of a circle. After all if you draw a polygon with 100 sides, say, then it is getting to look very much like a circle. In fact it would be hard to see the difference. And that’s the point. There is very little difference between the area of a regular polygon with n sides and perimeter 30 cm, where n is large, and the area of a circle with perimeter 30 cm.
| Attachment | Size |
|---|---|
| PolygonalStrings.pdf | 39.96 KB |
| PolygonalStringsMaori.pdf | 42.33 KB |
Similar Resources
Peter's Third String
Determine the maximum area of a rectangle with a given perimeter
Consider how the area of a quadrilateral changes as its shape changes
Interpret a relationship from a graph
The Old Chicken Run Problem
use algebraic equations to determine the maximum area of a rectangle with a given partial perimeter.
From a Square to a Rectangle
Solve problems involving percentage increases and decreases
Apply the area formulas for squares and rectangles
Devise and use problem solving strategies to explore situations mathematically (be systematic, use a diagram).
Peter's Second String
determine the maximum area of a rectangle with a given perimeter
determine the range of areas of a rectangle with a given perimeter
pose questions for mathematical exploration
prove or refute mathematical conjectures
Peter's String
Determine the area of a rectangle with a given perimeter;
Pose questions for mathematical exploration
Make conjectures in a mathematical context
Prove or refute mathematical conjectures
