Polygonal strings
This problem solving activity has a number and algebra (equations and expressions) focus.

It is 30 cm long.
He plays with it and makes different shapes all with the same perimeter of 30 cm.
Then he wonders about polygons.
Which has the biggest area: an equilateral triangle, a square or a regular hexagon?
His sister Kiri says that she thinks he can get more area inside a circle with that perimeter.
Which of these figures has the biggest area?
- Determine the maximum area of a regular polygon with a given perimeter.
- Appreciate the concept of limit as it applies to the area of regular n-gons and circle that both have the same perimeter.
This problem explores the areas of regular polygons with a fixed perimeter, and shows that they are ‘bounded above’ by the circle with the same perimeter. To solve the problem students must be able to calculate areas of triangles using the formula: area = ½ base length x height, and the area of a circle from a given circumference, using the formula AC = πr2.
It would be an advantage if students have experienced using algebraic equations to solve problems such as Peter’s Third String, Level 6.
The extension problem introduces the idea of limit and so is useful as background or introduction to the gradient of a curve. The idea of gradient and its many applications, occupies a prominent place in calculus at Levels 7 and 8.
Mathematics is more than doing calculations or following routine instructions. Thinking and creating are at the heart of the subject. Though some problems have a set procedure or a formula that can be used to solve them, the most worthwhile problems require the use of known mathematics in a novel way.
There are seven problems related to perimeter and area.
The first set includes: Peters’ String, Measurement, Level 4; Peters’ Second String, Measurement, Level 5; The Old Chicken Run Problem, Number and Algebra (Equations and Expressions), Level 6; and Peters’ Third String, Number and Algebra (Equations and Expressions), Level 6. These show the non-link between rectangles’ areas and perimeters, including showing that among all quadrilaterals with a fixed perimeter, the square has the largest area.
The second set includes: Karen’s Tiles, Measurement, Level 5 and Karen’s Second Tiles, Number and Algebra (Equations and Expressions), Level 6. These problems explore maximum and minimum perimeters for a given area.
The Problem
Peter keeps a piece of string from a parcel that came for his birthday. It is 30 cm long. He plays with it and makes different shapes all with the same perimeter of 30 cm. Then he wonders about polygons. Which has the biggest area: an equilateral triangle, a square or a regular hexagon?
His sister Kiri says that she thinks he can get more area inside a circle with that perimeter.
Which of these figures has the biggest area?
Teaching Sequence
- Introduce the problem to the class. Have them consider how they might approach the problem.
- Let the class investigate the problem in any way that they want. Give help, as appropriate, as they begin to record their diagrams and equations.
- Check on groups' progress as they work. Encourage them to draw large diagrams to show clearly what is going on and to keep a record of their work. Help them with the idea of breaking polygons down into triangles
- If a number of students are struggling, a brainstorming session may help.
- The extension problem covers an important idea about limits that should be shared with all of the class.
- Share and discuss the students’ answers. Have them to write up their work, making sure that they have carefully explained their arguments.
Extension
If Peter makes any regular polygon shape with his string, what is the maximum area he can make?
Can he get an area that is bigger than the area of the circle with perimeter 30 cm?
Solution
Work out the areas of an equilateral triangle, a square, a regular hexagon and a circle, all of which have a perimeter of 30 cm.
Equilateral triangle:
As the perimeter of the equilateral triangle below is 30 cm, one of its sides must be 10 cm.
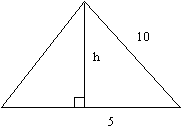
If we draw the perpendicular of the triangle, we see that, by Pythagoras’ Theorem, 102 = 52 + h2. So, h2 = 102 – 52 = 100 – 25 = 75. So h = √75. The area of the equilateral triangle is, therefore, AT = ½ x 10 x √75. This is approximately 43.30 cm2.
Square:
If a square has four sides and perimeter of 30 cm, one of its sides has length 7.5 cm. So its area is AS = 7.5 x 7.5 = 56.25.
Regular hexagon:
The regular hexagon below has a perimeter of 30 cm, and six equal sides, so each side must be 5 cm in length.
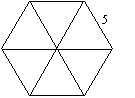
It is probably easiest to divide the hexagon into six equilateral triangles, each one of which has side length of 5 cm. Using ideas from above, we see that the area of each of these triangles is ½ x 5 x √(52 - 2.5 2). This is approximately 10.83 cm2. So the area of the regular hexagon AH = 6 x 10.83 = 64.95.
Circle:
If the perimeter of a circle is 30 cm, then we can find the radius using 30 = 2πr. So r = 30/2π = 15/2π. Leave this in this form for the moment. The area of the circle is then AC = πr2 = π(15/π)2 = 152/π = 225/π = 71.62.
It is clear that the circle has the biggest area. It’s interesting that the areas of the regular polygons seem to increase as the number of sides increases.
Solution to the Extension
Suppose that we look at a regular n-gon. In other words a regular polygon with n sides. As its perimeter is 30 cm, then one of its sides must have length 30/n and half of one of its sides must be 15/n cm long.
The diagram below shows one of the n isosceles triangles that make up the regular n-gon. Since n triangles together make up 2π at A, the angle (in degrees) in each triangle is 2π/n. So the angle BAC = 2π/n and the angle BAD is π/n.
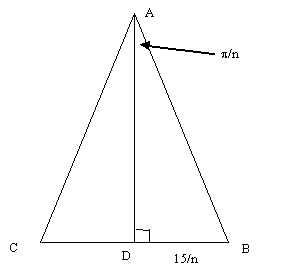
In the right angled triangle ABD, BD/AD = tan (π/n). So AD = BD/tan (π/n). And so the area of triangle ABC is BD. AD = BD2/tan (π/n) = [15/n]2/tan (π/n).
But we want the area of the regular n-gon which is formed from n triangles congruent to triangle ABC. This area is therefore AN = n{(15/n)2/tan (π/n)} = 225/[n tan(π/n)].
Let’s check to see that we haven’t made any errors here by using n = 3, 4 and 6. In these cases we should get the same values that we got for the equilateral triangle, the square and the regular hexagon.
n = 3: AN = 225/[3 tan(π/3)] = 225/3√3 = 25√3 = 43.30.
n = 4: AN = 225/[4 tan(π/4)] = 225/4 = 56.25.
n = 6: AN = 225/[6 tan(π/6)] = 225√3/6 = 75√3/2 = 64.95.
Since we do, then there is a very good chance that we have made no mistakes so far!
So AN = 225/[n tan(π/n)]. Is it obvious what value of n gives us a maximum value? You might like to program a computer to run off values for n up to say 100. It may be possible to do this if you have some calculus under your belt but that is not likely at Level 6. So you may have to rely on a table showing you that the values of AN actually keep increasing as n increases. In that case there is no biggest polygon.
Having said that though, we can show that AN is never bigger than a certain value. The thing that you need to know is that for q small, tan q is very close to being equal to q. Let’s use that approximation to see what happens.
AN = 225/[n tan(π/n)] » 225/n(π/n) since for n large, π/n is very small and so tan (p/n) is approximately equal to π/n.
Then AN » 225/n(π/n) = 225/π. Now the surprising thing is that this is the area of the circle with perimeter 30 cm!
One final thing, it runs out that tan(p/n) is always bigger than π/n. So AN is always slightly less than 225/π. We can make a regular polygon with perimeter 30 cm that is as close as we like to the area of the circle with the same perimeter but it will never quite be as big.
It at least makes sense that the area of a polygon with a large number of sides can approximate the area of a circle. After all if you draw a polygon with 100 sides, say, then it is getting to look very much like a circle. In fact it would be hard to see the difference. And that’s the point. There is very little difference between the area of a regular polygon with n sides and perimeter 30 cm, where n is large, and the area of a circle with perimeter 30 cm.