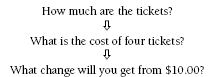Playing with Numbers

Problem One

Most students are likely to use trial and improvement strategies to solve this problem. Some thinking about the operations and the size of the numbers involved would be very productive.
Much of the equation for the answer 12 is likely to be made up by the product of  x . Looking for two numbers with a product close to 12 will limit the possibilities, for example, 7 x 2.
Students may like to investigate what other answers are possible by putting the digits in different positions.

Problem Two

In this problem, students must pay attention to the important information. Drawing a flow chart of the decision-making process might help:

Try changing conditions in the problem to check on the students’ understanding of the process, for example,
“Kim buys seven tickets and hands over a $20 note. How much change will he get?”

Problem Three

This problem could be modelled with counters so that students understand that the return journey from each flag must be included in the total distance. Encourage them to write their methods mathematically, for example, 12 + 24 + 36 + 48 = .
To check if they have generalised the process, ask: “How far would you run in total if there were two more flags to run to?” 12 + 24 + 36 + 48 + 60 + 72 = 
Encourage students to look for patterns. For example, some may express the solution using multiplication by six:
(2 x 6) + (4 x 6) + (6 x 6) + (8 x 6) + (10 x 6) + (12 x 6)
= 42 x 6
= 252

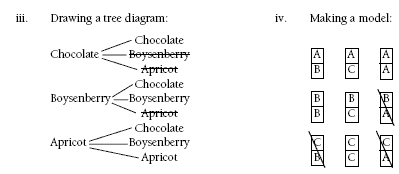
Problem Four

Making a physical model of the problem with counters or similar apparatus may help students find all the possibilities. Some discussion may focus on whether chocolate and boysenberry is a different ice cream to boysenberry and chocolate. In the explanation below, the two ice creams are considered to be the same, and duplicates are eliminated.
Students could use various strategies:

All these strategies are valuable. Encourage the students to generalise their approach  by asking, “How many different ice creams would be possible if banana ice cream were available as well?”

Answers to Problems

1. 7 x 2 + 3 – 5 or 2 x 7 + 3 – 5
2. $4
3. 120 metres
4. chocolate and boysenberry
chocolate and apricot
chocolate and chocolate
boysenberry and boysenberry
boysenberry and apricot
apricot and apricot