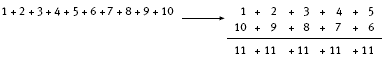This is a level 4 algebra strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (389 KB)
use a rule to describe a pattern
use a rule to make a prediction or continue a pattern
FIO, Level 4, Algebra, Book Two, Pegged Out, page 13
In this activity, students add consecutive numbers that represent distances of pegs from a starting position.
In question 1, the students must first understand the nature of the relay competition. This means that they ust see that for a race with 15 pegs spaced 1 metre apart, each competitor must carry pegs a total distance f 120 metres, which is found from 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15.
In question 2, they are likely to use a trial-and-improvement problem-solving strategy to work out that if each competitor were to run 210 metres carrying pegs, there must be 20 pegs involved. In question 3, however, they follow the beginnings of Trudie’s short cut to work out how far each competitor must run carrying pegs when there are just 7 pegs. Trudie’s short cut is reasonably sophisticated and may require some discussion to help the students understand how it works. In question 3b, they see if they can extend Trudie’s reasoning to a race with 19 pegs.
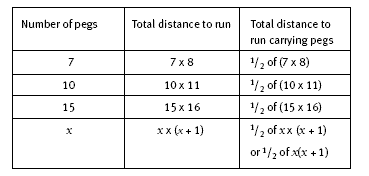
The patterns in the table below show how the rule given in the Answers can be extended to a race with x pegs.
When a race has 50 pegs, the distance each competitor must run carrying pegs is 1/2 x 50 x 51, which is 1/2 x 2 550, or 1 275 metres.
Some students may be interested in exploring ways to add consecutive numbers. At the age of 7, in his first year at primary school, Carl Friedrich Gauss (1777–1855), who later became one of the world’s greatest mathematicians, suggested to his teachers a way to add the numbers from 1 to 100. For numbers from 1 to 10 rather than 1 to 100, his short cut is:
The sum is then 5 x 11 = 55. For the numbers from 1 to 100, it is 50 x 101 = 5 050
Answers to Activity
1. 120 m. (1 + 2 + 3 + 4 … + 14 + 15 = 120 m. They run 240 m but only carry a peg for half that distance.)
2. 20
3. a. The calculation 7 x 8 = 56 is the total distance in metres run with and without pegs. So 28 m, which is 1/2 of 56 m, is the distance run with (or without) pegs.
b. 190 m. (1/2 of 19 x 20)
4. a. A possible rule is: add 1 to the distance to the last peg, multiply this by the number of pegs, and then halve the result. (Note that the distance to the last peg is the same as the number of pegs. This could be the basis for another rule.)
b. 1 275 m. (51 x 50 ÷ 2)