This unit is about generating number patterns for certain creatures from the mythical planet of Elsinore. Each ‘Pede’ is made up of square parts and has a number of feet. The patterns range from counting by 2s and 3s, to being the number of feet plus three.
- Continue a simple pattern
- Generalise the pattern.
Patterns are the basis of much mathematics. There is always a need to find a link between this variable and that variable. This unit provides an introduction to pattern in the context of mythical creatures. Ākonga are given practice in finding the next creature in a sequence. This leads to the main aim, which is for the ākonga to begin to see the link between the number of feet that certain creatures have and the number of squares that make them up.
One of the things that is deliberately attempted here is for ākonga to see the link above in both directions. Not only do ākonga get practice in linking squares to the number of feet, but they also are asked to try to find the number of feet that a creature with a certain number of squares has.
This unit provides an opportunity to develop number knowledge in the area of Number Sequence and Order, in particular development of knowledge of the forward number word sequence and skip counting patterns.
This unit can be differentiated by varying the scaffolding provided or altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
- providing ākonga with additional time to explore the patterns and/or by making, drawing and counting pede, before expecting them to continue the patterns using only numbers
- encouraging ākonga to design their own mythical creatures and explain their number patterns to others
- having ākonga work with pede that involve simple number patterns. Other simple alternatives include:

The context of this unit can be adapted to address diversity, and to appeal further to the interests and background experiences of ākonga. For example, ākonga may like to colour their pede with their favourite colours or decorate them with culturally significant patterns that you have learnt about. Picture books such as Taniwha by Robyn Kahukiwa could be used to introduce the idea of a mythical creature, and could lead to further learning about myths and legends from cultures relevant to your ākonga. If the context of mythical creatures is inappropriate for your āklonga, then the context of native animals could be used instead.
Te reo Māori vocabulary terms such as tauira (pattern) and tau (number) could be introduced in this unit and used throughout other mathematical learning.
- Tiles
- Squares of coloured paper
As each pede is developed, help ākonga focus on the number patterns involved by creating tables as below. Similar tables can be drawn for each type of pede.
Humped Back Pede | |
Number of Feet | Number of squares |
1 | 2 |
2 | 4 |
3 | 6 |
4 | 8 |
5 | 10 |
Use of a hundreds board may help ākonga visualise the number patterns more easily and help them to predict which numbers will be part of the patterns.
The conclusion of each session is an ideal time to focus on the number patterns involved. Questions to develop number knowledge include:
Which number comes next in the number pattern for this pede? How do you know?
Which number will be before 20 in this pattern? (or another number as appropriate)
How do you know?
What is the largest number you can think of in this pattern? How do you know?
Could a pede with 20 squares be a Spotted Pede? Why / Why not?
Could a pede with 32 squares be a 2-pede? Why / Why not?
Are there any numbers that could be Spotted Pedes and Humped Back Pedes? What are they? How did you work that out?
Session 1
Here we explore number patterns related to the mythical creatures that live on the planet Elsinore. The patterns involve skip counting by 2s.
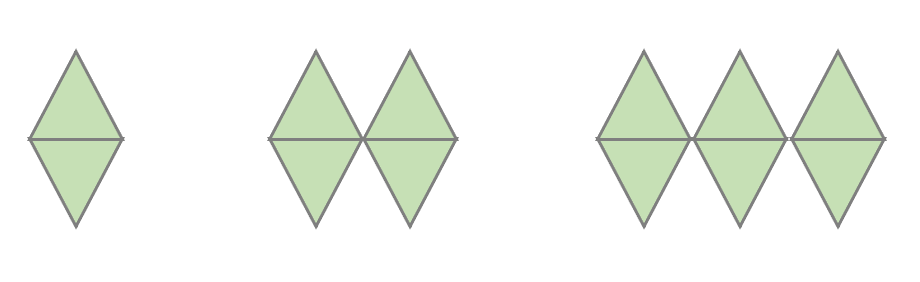
Introduce the idea of a mythical creature with a picture book like Taniwha by Robyn Kahukiwa, or Zog by Julia Donaldson. Consider whether a local iwi member could come to talk to your class about the history of taniwha in your local area. On planet Elsinore there lives a strange collection of creatures. There is the Humped-Back Pede. The Humped Back 1-pede looks like this. Can you see their eye? And the Humped Back 2-pede looks like this. They have an eye too. (Show your ākonga the pictures below.) Ask ākonga to work individually or in pairs (tuakana/teina model) to make a Humped Back 3-pede with the green tiles, or draw a picture.
Can you work out how many squares a Humped Back 4-pede has?

Gather ākonga together to talk about the creatures that they drew. Explore the number pattern of counting in 2s that comes from the Humped-Back Pedes. Also ask questions like:
Can you tell me how many green squares a Humped Back 5-pede will have?
Can you tell me how many green squares a Humped Back 7-pede will have?
Can you tell me how many green squares a Humped Back 10-pede will have?
How many feet has a Humped-Back Pede with 12 squares?
How many feet has a Humped-Back Pede with 18 squares?
How many feet has a Humped-Back Pede with 20 squares?
Can you tell me how to get the number of squares that a Humped-Back Pede with a particular number of feet has?
Can you tell me how to get the number of feet that a Humped-Back Pede with a particular number of squares has?
Session 2
Here we investigate some more mythical creatures that live on planet Elsinore. The patterns here involve skip counting by 3s.
- There are other creatures on the planet Elsinore. They look as if they have been made up from squares. The ones with one foot are called 1-pedes. The ones with two feet are called 2-pedes and the ones with 3 feet are called 3-pedes. (Show ākonga the picture below.)

- Did you know that ‘pede’ means ‘foot’?
How many feet would a 4-pede have? What about a 5-pede?
Can you tell me how many squares a 1-pede has?
How many squares does a 2-pede have?
What about a 3-pede?
(Put the numbers of squares beside the creatures as ākonga answer the questions, or create a table) - Can someone tell me what a 4-pede looks like?
How many feet will it have?
How many squares will it have?
Can someone make one for me with these square tiles?
Does everyone agree with that?
(Write 11 under the 4-pede.) - Let’s have a look at the number of squares that these Pedes have. Count them out. 2, 5, 8, 11.
I wonder what sort of Pede comes next? (5-pede.)
How many squares does a 5-pede have? (14)
I wonder what sort of Pede comes next? (6-pede.)
How many squares does a 6-pede have? (17)
Is there any pattern in the number of squares that Pedes have? (Add on 3 for each extra foot. Talk about skip counting by 3s.)
Session 3
Here we explore patterns further. Where we are particularly interested in linking the number of squares on a creature and the number of feet it has.
- Here we are going to explore the Spotted Pedes. This is what they look like. Talk about the number of squares they have, and the number of blue and red squares. Record these beside each of the Spotted Pedes.

- Ask ākonga to draw or make the Spotted 4-pedes? As they work ask them the following questions:
How many red squares does a Spotted 4-pede have?
How many blue squares does a Spotted 4-pede have?
How many squares are all together? How did you work that out?
Why are there more blue squares than red squares? How many more? - Repeat with Spotted 5-pedes and Spotted 6-pedes.
How many red squares does a Spotted 5-pede have?
Can you tell me how many blue squares a Spotted 5-pede has? Draw it.
How many red squares does a Spotted 6-pede have?
How many more blue squares does a Spotted 6-pede have? Draw it. - For those ākonga who need challenging, ask them about the Spotted 10-pede?
These ākonga could also be encouraged to make a table of there mathematical thinking.
How many red squares does a Spotted 10-pede have?
How many blue squares does a Spotted 10-pede have? - At the end of the session spend time sharing findings as a class (mahi tahi). Ask ākonga:
What did you find out about the Spotted Pedes?
What patterns did you find?
(Try to get them to see that they have as many red squares as they have feet. This means that it is very easy to find out how many red squares they have.)
Session 4
- We are going to find out about the Big-Headed Pedes. This is what they look like.
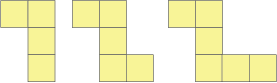
- Ask ākonga to work with a partner (tuakana/teina model could work well here) to draw the next three Big-Headed Pedes (4, 5, 6). As they work, ask ākonga the following questions:
How many yellow squares does a Big-Headed Pede 4-pede have?
How many yellow squares does a Big-Headed Pede 5-pede have?
How many yellow squares does a Big-Headed Pede 6-pede have?
Do you need to draw the creatures to work out how many squares they have? Why or why not?
Could you work out how many yellow squares a Big-Headed Pede 10-pede would have? - At the end of the session spend time sharing findings as a class (mahi tahi). Ask them:
What did you find out about the Big-Headed Pedes?
What patterns did you find?
(Try to get them to see that they have three more yellow squares than they have feet. This means that it is very easy to find out how many yellow squares they have.)
I saw a Big-Headed Pede with 16 yellow squares. How many feet did she have?
Session 5
- Can you tell me what kinds of Pedes we have been talking about this week?
Discuss the Pedes, the Humped-Back Pedes, the Spotted Pedes and the Big-Headed Pedes. - Ask ākonga to work with their partners (tuakana/teina model) to invent a Pede of their own. Ask ākonga to record the first three pedes on one piece of paper and the other three on a second sheet. Ask them to also invent a name for their creature.
- Pairs could then swap the first three Pedes to see if they can work out the next three Pedes for each other’s creature. They can then check with each other to see if they arrived at the same Pedes for the 4, 5 and 6 creatures.
- As time allows, ākonga could swap pedes with other pairs.
- As the pairs work, ask them to discuss the various patterns that they have produced. Ask them questions such as:
How many squares does one of your 5-pedes have?
Can you tell me the number of squares an X Pede with 10 feet (or some other relatively large number) has?
If I had 15 squares, what is the Pede with the largest number of feet that I could draw? - Collate the classes Pedes into a book of Pede problems that can be worked on by ākonga during any choosing time.
Dear parents and whānau,
In maths this week we have been working on patterns. We have looked at some mythical creatures from the planet Elsinore. We have seen the patterns that their numbers of squares have. Here is a creature from Elsinore. Together you could explore the links between its number of legs and the number of squares that make up its body.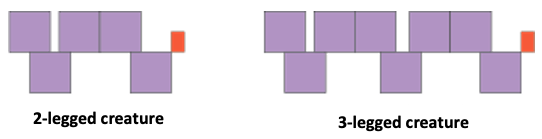
Discuss with your child how many squares does a 2-legged creature have?
How many squares does a 3-legged creature have?
How many squares does a 4-legged creature have?
How many legs does a creature with 20 squares have? Talk together about how you know? What do you have to do to work this out?
We would also like you to help us come up with a name for our creature. Write your ideas here.
We hope that you enjoyed working together on this algebra patterning task.