The purpose of this activity is for students to fit rectangles of a specified shape into a defined space according to identified criteria.
This activity assumes the students have experience in the following areas:
- Measuring lengths with metric units.
- Defining the properties of two-dimensional shapes.
- Creating three-dimensional models to scale.
- Form tessellations of two-dimensional shapes and explain why they work.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
.jpg)
A small business wants to build a customer carpark on the land in front of their shop.
The land is a 15 m by 12 m rectangle with road access on the short side. Each car park space needs to be 3 m by 5 m and cars need at least 4 m of clear space between rows to get in and out without incident.
Can you arrange a layout for the carpark that will allow for at least 8 cars to be parked on the space?
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- Do I understand the situation and the words? (Students may need to call on personal experience of carparks to make sense of the requirements, particularly why a clear space is needed and why each park needs to measure 3 m x 5 m.)
- Do I have all the information I need? Is anything missing?
- Do I have a sense of how big an area of 15 m by 12 m is? Do I need to measure this area out on the court? Do I have a sense of how big each car space is?
- What are the requirements for a solution? (There must be a carpark layout that parks at least 8 cars and allows room for access. The layout needs to be presented clearly to a reader.)
- Does this look/sound like a problem I have worked on before?
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- What strategies could I use? Do I need to build the carpark to actual size?
- Would making a model or drawing a diagram be useful strategies?
- What would need to be true about how my model or diagram is made? (Scale is important.)
- Could I use digital graphics as a useful tool?
- Does my model or diagram allow me to try different layouts?
- Can I share my ideas with others? How will that help me find the best solution?
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Have I recorded my ideas in a way that helps me to experiment with different layouts?
- What am I leaning about things that work and don’t work as I experiment?
- Am I considering the conditions properly each time, particularly to spaces for cars to get in and out?
- Have I assumed things about the car layout that aren’t necessarily true?
- How do my results look different to others? Why could this be?
- Does my solution make sense? Are there other possibilities?
- Is there another possible way to solve it that is more efficient?
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- What is my solution? Does it meet the requirements?
- Is it the best solution? Why?
- How would I convince someone else that I have the best layout?
- Could I have solved the problem in a more efficient way?
- Which ideas or tools worked well in my investigation?
- What could I try differently next time?
- What could I find out next? Is there some maths I need to learn?
Examples of work
Work sample 1
The student creates a scale model of the parking space using grid paper. They cut out rectangles to represent the parking space of one car and physically position the ‘parks’ on a 15 x 12 grid. The student creates several viable layouts.
Click on the image to enlarge it. Click again to close.
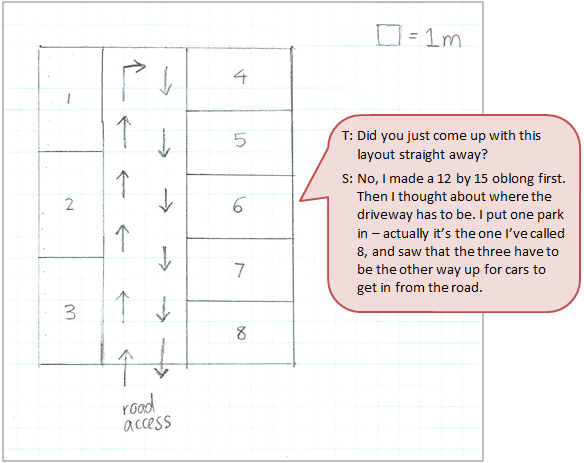
Work sample 2
The student creates a scale model of the parking space using measurements of 1 centimetre to represent 1 metre. They draw a diagram of a viable solution allowing for the practical consideration of car access from the road.