Copycats
Tessellate using squares and triangles
Describe the properties of tessellating shapes
Devise and use problem solving strategies to explore situations mathematically (guess and check, make a drawing, use equipment)
This is a simple example that investigates an idea to do with shapes that the students might not have normally met. It should help them explore basic shapes in a creative environment.
The first extension is a novel way to link their knowledge of geometry with patterns. The second extension is also useful in developing students’s thinking skills. For example, in the extension, they have a free rein to create any shapes they like that are copycats.
Problem
Simon has just discovered copycats. A square is a copycat because you can put four of them together to make another square.
Simon wondered if triangles and circles were copycats. What do you think?
Teaching sequence
- Ask: What is a copycat?
- Discuss the definition of copycat as it applies to this problem.
- Give the students (in pairs) an equilateral triangle and ask them to find out whether it is a copycat. Discuss the properties of an equilateral triangle (3 equal sides, 3 equal angles )
How do you know that they are equal? (fold and check) - Share findings.
- Pose the problem: Are all triangles copycats?
The students need to make their own triangle and see if it is a copycat. As they work ask:
What type of triangle are you using? (right triangle, scalene, isoceles, equilateral)
Describe the triangle that you are using?
Are circles copycats? Why do you think that? - Share findings.
Extension to the problem
- Simon talked to Ben about his copycats. Ben noticed that you needed four squares to make a bigger square and four triangles to make a bigger triangle. Could you make a square with any other number of squares? How many squares can you put together to make a square? Is there a pattern here?
- What other shapes are copycats?
Solution
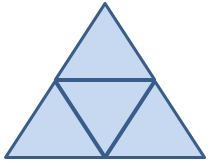
All triangles are copycats. This can be shown using four triangles as in the picture.
On the other hand, circles aren’t copycats. Having said that we have to prove it. The problem with circles is that when you put two of them together, they don’t fit. Clearly two circles don’t make a circle. So we need three at least. But three circles put together have lots of gaps. So there is no way that three or more circles can be put together to fill up all the space of another circle.
Extension 1:
It turns out that 4, 9, 16, 25, and, in fact, any square number of squares can be used. Why can’t a non-square number be used? Is this the same for triangles too or do you have to use triangle numbers there?
Extension 2:
The L-shape in the drawing below is a copycat. To check this out, put one L-shape around each of the top-left, bottom-left and bottom-right corners.
| Attachment | Size |
|---|---|
| CopyCats.pdf | 38.33 KB |
| CopyCatsMaori.pdf | 51.11 KB |
Similar Resources
Sol's Serviettes
Use the areas of triangles and squares to find unknown lengths
Devise and use problem solving strategies to explore situations mathematically (be systematic, draw a diagram).
Flip's Flag
apply the angle properties of squares, rectangles and triangles
use fractions to express the relationships between the areas of rectangles, squares and triangles
devise and use problem solving strategies to explore situations mathematically (be systematic).
The Five Number Game
Explain what it means to square number.
Explain what it means to cube a number.
Define prime numbers using their own language.
Devise and use problem solving strategies (use equipment).
Polygonal Strings
This is a problem from the number and algebra strand.
Square Milk Bottle Crates
Find a rule for a quadratic pattern
Justify or explain the rule for a quadratic pattern
Devise and use problem solving strategies to explore situations mathematically (be systematic, draw a diagram, use a table, use algebra).
