Outlining Area
This unit of work begins with an exploration of shapes that can be made with centimetre cubes. We draw around classroom objects then use centimetre squared paper to work out the area of their outlines.
recognise the need for a standard unit of area
measure surfaces using square centimetres
estimate the measure of surfaces using square centimetres
When students can measure areas effectively using non-standard units, they are ready to move to the use of standard units. The motivation for moving to this stage, often follows from experiences where the students have used different non-standard units for the same area and have realised that consistency in the units used would allow for the easier and more accurate communication of area measures.
Students’ measurement experiences must enable them to:
- develop an understanding of the size of a square metre and a square centimetre;
- estimate and measure using square metres and square centimetres.
The usual sequence used in primary school is to introduce the square centimetre and then the square metre.
The square centimetre is introduced first, because it is small enough to measure common objects. The size of the square centimetre can be established by constructing it, for example by cutting 1-centimetre pieces of paper. Most primary classrooms also have a supply of 1-cm cubes that can be used to measure the area of objects. An appreciation of the size of the unit can be built up through lots of experience in measuring everyday objects. The students should be encouraged to develop their own reference for a centimetre, for example, a fingernail or a small button.
As the students become familiar with the size of the square centimetre they should be given many opportunities to estimate before using precise measurement. They can also be given the task of using centimetre-squared paper to create different shapes of the same area.
Getting Started
We introduce this unit with a guessing game.
- Show the students the outline of an object, for example; a small book, a pebbles packet or a calculator.
What do you think that this could be the outline of?
How many cubes do you think I would need to cover this shape? - Give each student a cube and ask them to write their guess on a piece of paper.
Show the class a shape made with 5 cm cubes.I think the area of the object is ......cubes
James T
Ask the students to record the shape on cm squared paper.
What is the area of this shape? - If the students say 5 squares tell them that the unit square is called a square centimetre.
Why do you think it is called a square centimetre? - Ask a volunteer to make a different shape with the 5 cubes. Tell them that the shape must be flat and the whole sides of the squares must touch.
What is the area of this shape? ( 5 square centimetres or 5 square cm ) - Give each student 5 cm cubes and challenge them to find other shapes that can be made with the cubes. Ask them to record the shapes on the cm grid paper.
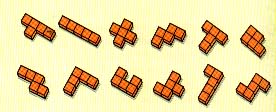
(These shapes are called pentominoes and there are 12 distinct shapes that can be made)
- Share shapes. Check again that the students understand that each has an area of 5 square cm.
Exploring
Over the next 3 days we figure out the area, in square centimetres, of the outlines of a variety of classroom objects
- Look again at the mystery shape from yesterday.
How can we work out who had the closest guess? - Give each pair of students a copy of the shape and ask them to work out its areas in square centimetres. Have available cm cubes and squared paper but let the students make decisions about how they will measure the area. Share areas and approaches used.
- Talk about how they are to handle part squares.
- Tell the students to write the area and their guess about the object on the shape. Display the shapes and measurements on a Mystery Object chart.
- With the class brainstorm objects that they think would have an area about the same as the mystery object. Write these on strips of paper. Put the strips of paper into a "hat". Working with a partner the students take a strip, make an outline of the selected object and calculate its area. Ask them to write the object name and measurement with the outline. At the end of each session order the objects measured from smallest to largest area.
- Add strips of paper to the "hat" which have different area measurements written. If the students select one of these they have to draw or find five shapes with that area.
Reflecting
Today we find out who has the largest foot.
- How could we find out?
About how many square cm do you think it would be? Why do you think that? - Ask small groups of students to think about a way of measuring feet to find out whose is the largest.
- When the outline is made the students need to work out the area of their foot.
- Share outlines and measurements. Display from smallest to largest.
Family and Whanau,
This week at school we have been measuring the area of objects using square centimetres.
At home this week your child is asked to figure out the area of largest and smallest footprints in your family using the attached square centimetre paper. They can draw and outline and then figure out the area. We will use these to make a classroom display of big and little feet and find the title holders of Big Foot and Little Foot.
| Attachment | Size |
|---|---|
| cmSquares.pdf | 29.15 KB |
Similar Resources
Making Benchmarks - Volume
In this unit we will explore the idea of having Benchmarks of 1 litre and ½ litre or 500 millilitres, to aid in estimating the volume of given objects.
How Can You Measure This?
In this unit students, working in groups of 2 to 4, carry out and report on a series of investigations involving decisions about how to measure something. The four investigations suggested are:
What’s In a Newspaper?
Students calculate what fraction of a newspaper is devoted to news, sport, advertisements and other categories of information.
Are You a Square?
Students determine whether their height is equal to, greater or less than, the distance from end to end of their outstretched arms.
How Far Do You Walk?
Students work out approximately how far they walk in one year.
How Thick Is It?
Students decide how to measure a length that cannot be measured directly – for example the thickness of a wall of their classroom.
In each investigation the students follow the same sequence:
- Make sure they understand the problem
- Discuss and decide on three different strategies for tackling the problem
- Complete a table to assess the merits of each strategy
- Use the best strategy for conducting the investigation
- Record their methods and results
Make a Measurement Maths Trail
In this unit students first go round a maths trail devised by the teacher. They then work in groups to devise and complete a maths trail of their own. They then go round this new maths trail or, if another class can work in parallel, each class goes round the other’s trail.
Great Grams
This unit comprises 5 stations which develop our concept of the "feel" of a gram. The stations may be taken as whole class activities or they may be set up as activities that groups of students use throughout the week.
Weighing Stations
In this unit students work at a variety of stations involving practical measuring tasks. Estimation skills and the ability to measure accurately using kilograms and grams are developed.
