These are level 3 statistics, geometry, algebra, and number problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (447 KB)
find outcomes using a tree diagram (Problem 1)
find rhombuses and trapezia in shapes (Problem 2)
continue a sequential pattern (Problem 3)
explore right angles on a clock face (Problem 4)
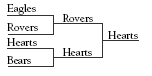
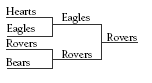
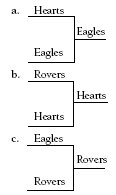
Problem One
a. Based on the information given, the Hearts must have beaten the Rovers in this tournament and the Eagles won the other preliminary game (because the Bears lost all their games). The Eagles did not lose to the Hearts, so they had to win the final.
b. The first game in the top half of the draw could go either way. There is no information about how the Eagles and the Rovers fare when they play each other. So either outcome is possible.
The second game is a definite win for the Hearts against the Bears, who lost all of their games. If you assume that the Eagles beat the Rovers, they would have played the Hearts in the final. This would make the Eagles the winners because they always beat the Hearts. However, the Eagles won the first tournament, so they cannot have won the second one (a different team won each tournament). So the only possibility, based on the information given, is that the Rovers won their first game and had to play the Hearts (for the reason above). In the final, the Hearts won, based on the information given (the Rovers lost to the Hearts).
.gif)
c. In the last tournament, the Rovers beat the Bears and the Eagles beat the Hearts (based on the information given). The final is the Eagles versus the Rovers. The Eagles have already won a tournament (see a), so the Rovers must have won this final.
Problem Two
The students need to first identify the rhombuses and trapezia in the shape. There is only one type of each: the rhombuses have side lengths of one stick and the trapezia are half the hexagon and comprise three triangles. The students can work systematically to count the rhombuses and trapezia. Drawing a diagram and marking the shapes may help to avoid counting any shape twice.
Problem Three
This question can be done (the long way) by writing out the alphabet backwards up to N and then assigning odd numbers from 1 up, starting at Z:
You’ll probably find that it’s slightly quicker to write the alphabet out starting at N and ending at Z. Then write down the odd numbers in order going backwards from 1 at Z.
Another way is to calculate how many letters there are from N to Z, inclusive. There are 13. The 13th odd number is 25.
Problem Four
Students who have trouble with this problem could first try Problem Three, page 9, in Problem Solving, Figure It Out, Level 3.
At any “o’clock”, the hour hand is always on the 12. The only way that the minute hand can make an angle of 90o with the hour hand is if it is on the 3 or the 9. So the only other right-angled o’clock is 3 o’clock. Some students may have suggested other times where the hour and the minute hands are 15 minutes away from each other, for example, 5 past 4 or quarter to 6. You may need to remind them that they have to find “o’clock” times, that is, where the hour hand is on 12. Also, at times such as 5 past 4 or quarter to 6, the hands don’t make a true right angle because the hour hand is not exactly on the hour number; it will be before or after that number.
Extension
“You could explore right-angled time. Can you have the two hands at right angles at some time other than 3 o’clock and 9 o’clock? Can you have a right-angled half hour?”
Hints for Students
1. Use each clue step by step. Be systematic.
2. Identify the rhombuses and trapezia in the hexagon. Now find a systematic way to count them.
3. How many of each letter are there? Can you see a pattern?
4. Can you see a right angle? For part b, make sure you have a perfect right angle each time. You could experiment with equipment or a diagram.
Answers to Problems
1.
2. a. 6
b. 6
3. 25
4. a. The angle between the hour and minute hands is 90o or a right angle.
b. The only other right-angled o’clock time is 3 o’clock.