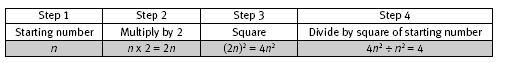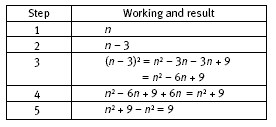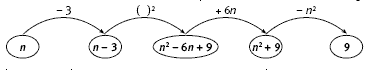Number Juggling

In this activity, students follow sets of instructions to verify two mathematical claims. In Challenge One, it is claimed that the answer is always 4, no matter what starting number is used, and in Challenge Two, it is claimed that the answer is always 9. (If the students try this with 1 or 2 as the starting number, they will find that this is also true when negative numbers are involved.)
The challenges presented here rely on generating an answer that does not depend on the starting number chosen. In each case, the process will first disguise the chosen number and then “strip away” this initial number to leave the final answer.
For example, a simple challenge would be:
Step 1: think of a number
Step 2: multiply by 6
Step 3: divide your result by twice the number you first thought of.
Your answer must be 3.
If the number chosen is 4, then we have:
Step 1: 4
Step 2: 4 x 6 = 24
Step 3: 24 ÷ (2 x 4) = 3
In this case, the original number is disguised in some way (it is multiplied by 6 in step 2) and then the original number is removed from the result (by division in step 3).
Algebraically, if n is our chosen number, we have 6n at the end of step 2 and 6n ÷ 2n = 3 at the end of step 3.
The example shown above is simpler than those in challenges One and Two, but the principle is the same.
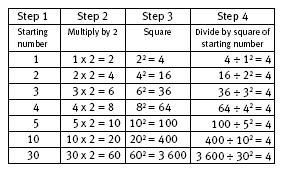
In Challenge One, students might set out a table as shown in the Answers to check the results for several different starting numbers. A further row, which shows the general rule, is:

The advantage of considering the situation algebraically is that it allows us to see clearly how the process used in the challenge works.
For example, both steps 2 and 3 disguise the initial number (first by multiplying by 2 and then by squaring the result) so that by the end of step 3, we have a number equal to 4n². In order to remove the initial number from the result, we divide by n². to give an answer of 4.
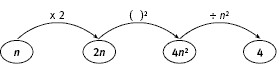
Another useful tool to show how the challenge works is a flow chart. The flow chart below shows how the sequence of instructions in Challenge One works.

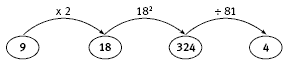
The students might follow the flow chart steps, choosing any value for the starting number, n. The next flow chart shows the steps when the starting number is 9:

After they have completed a few flow charts with particular values for n, the students could again consider the first flow chart with the aim of reinforcing their understanding of why the challenge works. They will see that an expression involving n occurs in each of the first three steps: in step one, n is chosen, in steps two and three, n is somehow disguised. In step four, n is removed from the expression (the expression 4n² is divided by n². to give 4) to give the final result.
The table in the Answers helps to show how Challenge Two works. Notice that the smallest starting number is 3. If it were less than 3, step two would lead to a negative value. This would increase the level of difficulty, but it would not alter the mathematics involved.
The results in the table given in the Answers confirm that, for a range of starting numbers, the result is always 9. Although the algebraic “proof” for this result is likely to be beyond most students at this stage, it is nevertheless shown below:

The flow chart below shows how the sequence of instructions in Challenge Two works:

This next flow chart shows the steps when the starting number is 9.

In the Investigation that follows the challenges, the students try to make up number challenges of their own. Flow charts can help the students see the effect of each operation clearly.

Answers to Activity

Challenge One
Each starting number produces the answer 4 (in step 4). The starting number is disguised by two multiplication steps and removed by division to give the answer of 4.

Challenge Two
Each starting number produces the answer 9 (step 5). The starting number is disguised by a mixture of subtraction, multiplication, and addition and then
removed by multiplication and subtraction to give the answer of 9.

Investigation
Challenges will vary. In all cases, the original number will be disguised in some way (for example, by multiplication) and then removed in the course of the final step or steps (for example, by division).