This problem solving activity has a logic and reasoning focus.
She plays this game with Tane.
First she puts a carton in, and then he does.
They keep alternating in this way.
However, the rule is that no three cartons can be in a line.
The winner is the one who puts the last carton in the crate.
If Hannah always goes first, who should always win, Hannah or Tane?
- Analyse a game.
For students to play this game successfully requires them to make a systematic analysis of all the possible arrangements of items within a 3 x 3 grid, given certain contingencies.
It may be useful for students to complete another problem in the series if they have not already done so, as this problem builds on earlier experiences. Students may also benefit from exploring Take Two, Algebra, Level 3, as this problem develops students' understanding of game playing strategies.
This problem is the final in this series of Logic and Reasoning problems: Strawberry Milk, and Chocolate Milk, Level 1; Three-In-A-Line, Level 2; No Three-In-A-Line, Level 3; More No-Three-In-A-Line, Level 4 and No-Three-In-A-Line Again, Level 5 and No-More-In-A-Line, Level 6.
- Coloured pens and paper
- Bottles tops
- Copymaster of the problem (Māori)
- Copymaster of the problem (English)
- Copymaster of 3 by 3 crates
- Copymaster of 4 by 4 crates
The Problem
Hannah has a square crate that can hold 9 cartons of milk.
She plays this game with Tane. First she puts a carton in, and then he does. They keep alternating in this way.
However, the rule is that no three cartons can be in a line.
The winner is the one who puts the last carton in the crate.
If Hannah always goes first, who should always win, Hannah or Tane?
.gif)
Teaching Sequence
- Pose the problem and discuss the symmetry of the crates.
Ask if they have played similar games, and strategies they may have used previously for other no-three-in-line problems. - Have students play a series of games to see if they can find a pattern. Is there a winning strategy for either player?
- Discuss as a class the strategies they have come up with.
- Try to get them to see the systematic approach shown in the Solution.
- Encourage students to attempt the extension problem.
- Have some groups report back to the class by illustrating their strategies for the game.
- Allow the students time to write up their solutions to the problem.
Solution
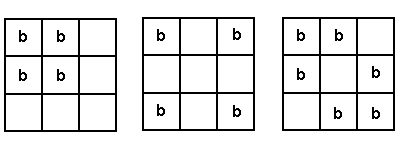
Tane knows that the only way that he can win is if he forces the game to stop after 2, 4, or 6 cartons have been added to the crate. But from No-Three-In-A-Line Again, he knows that it has to be 4 or 6. So he is going to try to force the cartons (b) into one of the positions below, or a position that is symmetrical with one of these positions.
On the other hand, Hannah will win if she can get the game to go to an odd number – 3 or 5. But she knows that 3 isn’t possible. So she has to look for one of the 5 carton positions below.
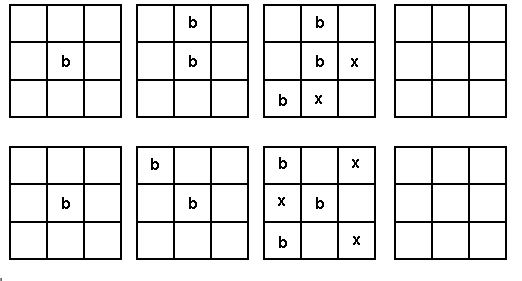
This game can now be analysed using the fact that a 3 by 3 crate essentially has only three different kinds of squares: (i) a corner square; (ii) a middle square on a side; and (iii) the centre square. This means that Hannah only has three starting moves. But the centre square move is powerful. Although they both only have one winning end-game with a carton (b) in the centre square, Hannah is able to force the game to go her way. Watch.
Hannah plays the centre square. Now, by symmetry, Tane has only two moves that he can make. In Game 1 above he plays in the middle square on an edge. In Game 2 he plays in the corner square.
To win, Hannah only has to put in a carton so that Tane’s winning position can’t be achieved. In both cases she plays in the corner as shown. Crosses show where Tane can’t play. Now wherever Tane plays, Hannah can finish the game by completing the crate as above. Hence Hannah can always win.