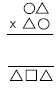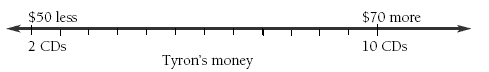Mystery Amounts

Problem One

The students will probably find the answer to this problem by experimenting, but they can use logic and reasoning to narrow down the scope of their experiments. The method outlined below shows what the answer is and also shows that there is only one possible answer. The students might want to follow it through to the end, but it is probably quickest to use the first step to eliminate some options and then experiment to find the correct answer.
Problem Two, page 16, in Problem Solving, Figure It Out, Level 3, could be a useful warm-up for this problem.
are “mirror numbers” because the digits are reversed. Mirror numbers are number pairs such as 23 and 32, 45 and 54, 19 and 91, and so on.
In this problem, you are looking for a mirror number where the product of the two reflections is less than 999. Writing out the calculation as long multiplication helps to visualise the problem:

There is no point in looking at numbers less than 10. Using numbers less than 10 (for example, 09 x 90 = 810) will always result in a 0 as the last digit of the answer and a non-zero number as the first digit. This does not fit in the pattern you are looking for, where the product is .
Other trials:
• 10 x 01 = 10: no good.
• 11 can’t be used because the digits in x must be different.
• 12 x 21 = 252: this is it. It fits the pattern.
 

But is this the only solution? Look at how the numbers work in 12 x 21 = 252.

The units digit of 252 is made up from the multiplication of the units digits of each number in the mirrored pair (2 x 1). The hundreds digit is made up by the tens digits of the reflections (1 x 2). This only works for a mirror number where one of the digits is a 1. So this limits you to the range 13 to 19 and then 31, 41, and so on.
Now you need to look at the middle digit of the product. It is formed using the digits of just one of the reflections. For example, for 12, square the units digit and add it to the square of the tens digit: 1 x 1 + 2 x 2 = 1 + 4 = 5. (Look back at your long multiplication model if you are unsure how this works.) This means that you cannot have a number where the sum of these two squares is greater than 9, otherwise there will be a carry over (for example, for 13, 1 x 1 + 3 x 3 = 1 + 9 = 10),
and the pattern is spoiled. This eliminates all the possibilities except 12 and 21, so the solution 12 x 21 = 252 is unique.

Problem Two

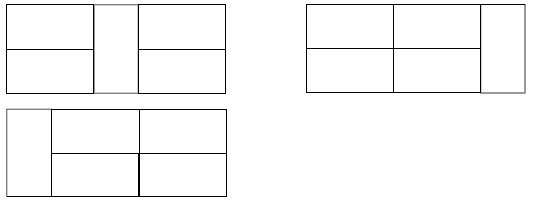
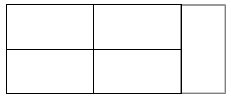
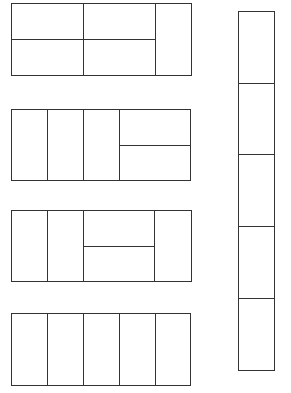
The mats are twice as long as they are wide. Each mat can be arranged horizontally or vertically. The students should work systematically to find the different possible arrangements of mats. If all of the mats are horizontal, you can only make one rectangular arrangement out of them:

If one of the mats is vertical and the rest are horizontal, there are three possible rectangles:

But note that the first rectangle is the same as the one shown in the problem, and the third one is a rotation of the second one, so there is only one new arrangement of the mats:

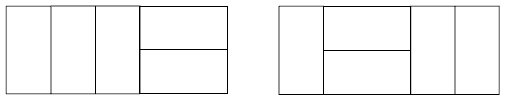
If two of the mats are vertical and three are horizontal, there will be one horizontal mat sticking out, so it’s impossible to make a rectangle. The same is the case with four vertical mats and one horizontal mat:

If three mats are vertical and two horizontal, there are two new mat arrangements:

If all five mats are vertical, this gives one more new arrangement:

So there are five ways of arranging the mats in addition to the arrangement in the students’ book.

Problem Three

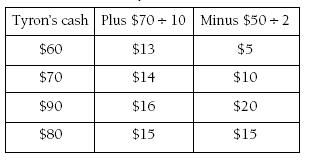
Tyron must have had more than $50, because the second clue says that if he had $50 less, he could still buy two CDs. Recording their trials on a table will help the students to find the correct answer quickly.
In the first column, put the trial amount for Tyron’s cash. In the next column, add $70 to the trial cash amount and divide the total by 10. That will give the cost of one CD. In the third column, subtract $50 from the trial cash amount and divide the total by 2. This will also give the amount of one CD. When the cost of one CD is the same in the last two columns, the students have found out how much cash Tyron had and the cost of one CD.

A CD costs $15, and Tyron had $80.
Another way of solving this is as follows:
Regardless of how much cash Tyron had to begin with, the difference between having $70 more and having $50 less is $120. The students could check this by plotting it on a number line.

The number line shows there is a difference of eight CDs being bought, so eight CDs cost $120.
One CD costs $120 ÷ 8 = $15.
If Tyron had $50 less, he could buy 2 CDs, which cost 2 x $15 = $30.
So he had $30 + $50 = $80 to begin with.

Problem Four

Most students will need to use trial and improvement. However, if you add 90 and 76 and 82, you’ll get 248, which is the combined total when each person is weighed twice, as in the illustration. Half of this is 124 kilograms, the combined mass of the three friends.
John and Trish weigh 90 kilograms. 124 – 90 = 34. So Zoe weighs 34 kilograms.
John and Zoe weigh 76. 124 – 76 = 48. So Trish weighs 48 kilograms.
Zoe and Trish weigh 82. 124 – 82 = 42. So John weighs 42 kilograms.

Hints for Students

1. You could use trial and improvement. Think about what happens when you multiply two two-digit numbers. Does this help you find the answer?
2. Use equipment or draw diagrams to experiment with different arrangements.
Work systematically. Two arrangements are considered the same if they are rotated or can be reflected onto each other.
3. Use a number line to model what is happening in this problem.
Think about how many CDs Tyron can buy when he has the smallest amount of money and how many he can buy when he has the largest amount of money.
4. You can use trial and improvement. Another strategy is to add all the weights
together. This will give the total of each person weighed twice. Can you use this to find each person’s weight?

Answers to Problems

1. The equation is 12 x 21 = 252.
2. There are five other different arrangements apart from the one on the page:

3. a. $15
b. $80
4. Trish: 48 kg
John: 42 kg
Zoe: 34 kg