In this unit students explore the commonly held belief that if anything bad can possibly happen, it will, and at the most inopportune time. They are encouraged to look at events involving chance and predict the likelihood of certain outcomes by both trialling the event and analysing it theoretically.
- Use simulations to investigate probability in common situations.
- Predict the likelihood of outcomes on the basis of an experiment.
- Determine the theoretical probability of an event.
This unit takes an interesting approach to probability by investigating some commonly held myths that can be thought of as going under the name of Murphy’s Law. It is likely that some of your students will have heard about Murphy’s Law and some of them will even have seen posters about it. The basic tenet presented is that what can go wrong will go wrong.
A series of practical situations are explored experimentally to test examples of Murphy’s Law. The students are encouraged to work out these situations theoretically too. Hence students get a chance to test and explore widely held views under experimental conditions.
Research indicates that people develop subjective feelings about situations based on their experiences. In the case of Murphy’s Law people are more likely to remember adverse outcomes than favourable ones. In this unit students are encouraged to contrast their beliefs with the outcomes of experiments.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- beginning with simple situations and moving to more complex situations
- acting out the situations
- modelling ways to record the events, such as using tally charts
- using spreadsheets to collate large numbers of trials and display the results in proportional displays pie charts and strip graphs help students recognise the part-whole fractions involved
- explicitly teaching students about ways to model all the possible outcomes, such as with the use of tree diagrams and tables
- providing opportunities for small group and individualised support and direct teaching of new and complex concepts
- asking students to conduct the experiments and discussions in collaborative groups
- providing calculators to ease the cognitive load associated with calculation
This unit is focussed on situations in which unwanted events occur. The unwanted nature of the events is known to have a subjective effect on students’ beliefs about likelihood. That provides an ideal opportunity to contrast those beliefs with actual outcomes. Students will relate to other situations that have adverse outcomes or, conversely, be interested in positive events that are likely to produce an opposite effect on beliefs. Situations like winning a game (rather than losing it), sunshine on a school trip (rather than rain), or landing a goal or seeing a favourite commercial (rather than missing it) may be more motivating for some students. You may wish to explore real world applications of Murphy’s Law in the teaching sessions following the unit. For example, through situations which relate to your students’ current interests, current events, or current learning from other curriculum areas.
Te reo Māori kupu such as tūponotanga whakamātau (experimental probability), tūponotanga tātai (theoretical probability), putanga (outcome), and whakamātau (experiment, test, trial) could be introduced in this unit and used throughout other mathematical learning
- Dice
- Red, green and orange counters
- Box
- Car keys
- Ice-cream containers
- Blank cubes
- Blank cards
- Copymaster One
- A pre-prepared spreadsheet
Getting Started
- Ask the students if they have heard of Murphy’s Law. Some of them may have heard their parents or other people refer to Murphy’s Law when something annoying has happened to them at a moment of great inconvenience. You might find an engaging video or text to introduce this concept to the class. Discuss the following events as examples of what we call Murphy’s Law:
- Being unable to find the car keys when you are in a hurry.
- Getting a flat tyre on your bicycle when you are many kilometres from home.
- Heavy rain in the afternoon when you did not take your coat to school (it was sunny when you left home in the morning).
- Missing the bus, train, or tram because it is early for a change.
- The first lesson will investigate the example of Murphy’s Law relating to keys. It goes like this (act it out as you are saying it):
You are carrying a heavy box of things to the door or to the car boot. You put the box in one arm to hold it while you reach inside your pocket for the keys and, you guessed it, the keys are in the other pocket! So, you shift the load onto the other arm to get the keys out or you become a contortionist by trying to get it with the opposite arm.
Murphy’s Law for keys says that keys are always in the pocket that you can’t reach. - Ask the students whether they believe in Murphy’s Law for keys and what we might do as an experiment to see if it is true or false. Record their ideas and negotiate a way to trial the event of the box and the keys.
One possibility would be to act out the selection of a side for both the keys and the box by randomly drawing a left or right card for each (make sure that there are two cards to choose from for each choice). Allocating heads to left and tails to right and tossing a coin for each would also work. - What are the chances of Murphy’s Law of keys happening?
Discuss ideas students have about how often the package and the key will be on the same side. - Let’s do an experiment to see how often Murphy’s Law applies.
How many trials do we need to check whether Murphy’s Law of keys is correct?
Ask students to keep a careful record of each trial. Each group of students can carry out ten trials and the results from all groups can be collated to give a large sample of results. The principle of a greater number of trials giving more reliable results should emerge. Collate the results using a spreadsheet.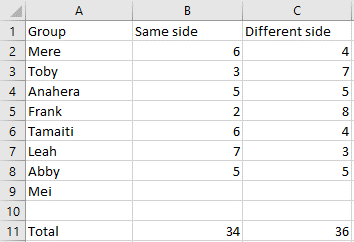
- What do you notice about the results?
Students might comment that the events (same and different sides) have similar frequencies (number of occurrences).
Why do you think this happens?
Let students discuss why they think the results are similar. Discuss students’ ideas. They might have some way to account for all of the outcomes. One example might be an organised list like this:
Left pocket-Left arm, Right pocket-Right arm, Left pocket-Right arm, Right pocket-Left arm.
Other ways to represent all the possible outcomes include a table or the tree diagram below. Note that there are four possible outcomes, and the two ticked ones indicate the keys being in the opposite pocket.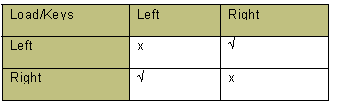
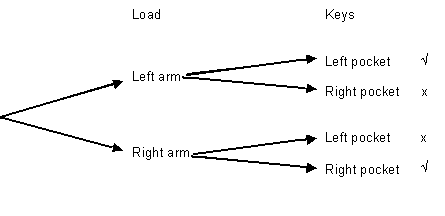
There are other factors at work with Murphy’s Law of keys that the students may or may not raise in the class discussion. Most people have a preferred arm for picking up things, usually the right arm. There is also a higher likelihood of the keys going in the right pocket since car ignition is usually on the right side and most people are right hand dominant (about 90%).
These considerations change the selection of the side for both pocket and load from being random. Discuss what random means. Random events are those in which all outcomes have the same chance of occurring. There is no influence on the chances of some outcomes happening more than others. The right-right combination is therefore much more likely than the other three.
The biased scenario could be tested experimentally.
One way is to select people at random and ask them to do these two things:- Hand them a set of keys and ask them to put them in their pocket.
- Give them a box to carry and ask them to take the box through a door that is shut.
This observation of people could be done as a homework assignment. It is wise to tell school students of the need to explain why they are conducting the survey to would-be participants.
- Collate the results from as many students or groups as possible. Ask the students to come up with a short report (e.g. in an oral, digital, video, written, diagrammatic, or acted-out format) of their findings about Murphy’s Law of keys. The report should include both the theoretical and the experimental results and a conclusion as to the validity of people’s belief in the Law. You could also use Copymaster One to emphasise a real-world context in which Murphy’s Law was believed in. This might motivate students to conduct more research into more local instances of Murphy’s Law.
Exploring
In this section of the unit, students explore some other examples of Murphy’s Law (shown below), and are encouraged to investigate examples of their own. Consider grouping students to encourage peer learning, collaboration, and productive learning conversations. Also consider how you can most effectively structure your session(s) around each of the ideas. There might also be examples of Murphy’s Law from your context that you wish to include instead of using all of the examples below.
Murphy’s Law of dice rolling
If you need to roll a six on a standard dice, to start a game, a six will take lots of rolls to turn up.
Discuss dice games where you need to roll a six to begin or get out of jail. Ludo is a good example (look online for a video).
- Is it harder to roll some numbers on a dice than others?
Take a class vote about which number, 1, 2, 3, 4, 5, or 6, is most likely to come up when you roll a standard dice. Expect that few students will think the next roll will be a six. That is in keeping with subjective beliefs about rolling a six. - Carry out an investigation to answer this question:
Is it harder to get a six than any other number on a standard die? - Gather the result of lots of dice rolls. There are many dice roll simulators online or you could do the real thing! Students are often sceptical about a computer simulation of a situation.
Murphy’s Law of Traffic Lights
If you are in a rush the traffic lights are always red when you get to them.
- This can be simulated by putting two red counters, two green counters, and one orange counter into an ice-cream container and then drawing a counter out at random. This gives you the colour of the lights on your arrival (probability of red is 2/5 = 40%). Your degree of haste can easily be simulated by rolling a dice (even numbers for rush, odd for lots of time), making up equal numbers of cards with rush and time on them and drawing one from a bag each time, or flipping a coin (heads for rush, tails for lots of time).
- In this case, students should observe that your degree of haste makes no difference to the likelihood of getting a red light. This brings up the issue of people believing in Murphy’s Law because unfavourable events in moments of crisis are much more memorable than favourable events in moments of tranquillity.
Murphy’s Law of Buttered Toast
The more expensive the carpet the greater the chance that the piece of toast that falls off your plate will land margarine side down.
This can be simulated easily using a coin for the piece of toast (heads for margarine side, tails for no margarine) and a money dice (faces of 10c, 20c, 50c, $1, 2 & on the blank face students can roll again). Alternatively use a flat object, such as an ice-cream container lid or a square piece of corrugated cardboard to be the piece of toast (labelled M for margarine on one side). Note that the outcomes of trials could be organised in a chart, like this:
Expense of Carpet Landed 10c 20c 50c $1 $2 Butter 5 2 5 3 7 Not Butter 7 5 3 5 5 - Students should realise that in this case the expense of the carpet has no impact on the theoretical probability of the bread landing butter side down. It is people’s recall of unfortunate occurrences that is responsible for this widely accepted corollary of Murphy’s Law.
- You might also discuss whether, or not, the situation is truly random. Since the toast will start its fall margarine side up, is it more likely to land margarine down, or is the probability really 50%?
Murphy’s Law of Tape
The more of a rush you are in the harder it is to find the start of a roll of tape.
Devise your own experiment to test out this version of Murphy’s Law. For an especially annoying variation use rolls of cellotape that have been exposed to light for some time.
Murphy’s Law of Drawing Pins
If a drawing pin drops on the floor the chance of it landing sharp end up increases as its distance to the nearest bare foot decreases.
- Encourage the children to discuss this and then devise an experiment to test it. This situation represents a relationship between distance from a bare foot and probability of getting a sharp end up result.
- Gather the class together to share the results of the simulation. Focus on the issue, Is Murphy’s Law of supermarket queues true or, like the traffic lights, a case of people only remembering when unpleasant things happen?
Reflecting
The final investigation relates to Murphy’s Law of shuffle play, the curse of all music lovers.
The Law states:
The more in love with a song you are, the less likely you are to hear it when you include it in a list of songs on shuffle.
- Discuss what 'shuffle' is. Many students will be familiar with online music-streaming services, which usually allow you to select a list of songs (e.g. a playlist, an album) and press ‘shuffle’, meaning the computer randomly chooses the next song to play.
- Let’s choose some songs to put on your playlist. Ask the students about their favourite songs at present. Make a short list of three songs to keep the situation simple. For illustration the possible songs are labelled 1, 2, and 3 based on preferential order from a class vote.
- Put bottle tops labelled 1, 2, and 3 in a bag or container (Note that all three bottle tops must be in the bag for a selection). Alternatively, look for a random number generator online and set it to select from 1, 2, and 3.
You only have time to hear four songs. What are the chances that you will hear the class favourite?
- Let students discuss their ideas. Most will say there is a high likelihood of Song 1 being heard seeing as there are three songs and four ‘slots’ for them to go in.
What are the chances of hearing the same song twice?
Students might believe that they will hear one song twice since there is one more slot than songs. Does that really occur? Ask students to work in small teams to generate 10 trials in which four songs are randomly selected. Ask them to record the results in a table like this:
Trial Result All songs Song 1 1 2 1 2 1 No Twice 2 1 3 3 1 No Twice 3 1 3 3 2 Yes Once 4 2 2 3 2 No None 5 3 2 1 3 Yes Once 6 3 2 3 2 No None 7 1 3 2 2 Yes Once 8 1 2 3 2 Yes Once 9 2 2 2 2 No None 10 3 1 1 2 Yes Twice - Is anything about your results surprising?
Students might notice that the occurrence of all three songs playing is less likely than they predicted. Students ready for extension might create a tree diagram to establish why the probability of all three songs playing is only 8/27. You could also do this with the whole class. Some might comment on surprising trials, such as 2,2,2,2. They might also comment that the favourite song (1) is not played in two of the ten trials. 2/10 = 0.2 = 20% is close to the theoretical probability of no playing of Song 1 (0.198).
- Would the probability of getting all songs and hearing song one change if we played five songs instead of four? Why?
Students should recognise that providing an extra slot will increase the chances of both events.
- Students might investigate what happens as they change both the number of songs and the number of playing slots available.
- Discuss advice for the music download company arising from the investigation.
Should the shuffle play only rely on selecting songs randomly?
How might the company use a customer’s ‘skip’ record to alter the probabilities?
How many songs make a good playlist that balances variety with hearing preferred songs?
- Complete the unit by discussing why Murphy’s Law is so popular.
Why is it that people think that the probability of something going wrong is greater than it really is?
Bring out the idea that feelings play a part in how we view probabilities. We tend to remember the times when things went wrong rather than the times things went well. If time permits, students could work in groups to create a representation of their learning about Murphy’s Law. This could be used to ensure that all students have developed sufficient understanding of using simulations to investigate probability, predicting the likelihood of outcomes on the basis of an experiment, and determining the theoretical probability of an event.
Dear parents and whānau,
At school this week we have been exploring Murphy’s Law. The basic idea behind Murphy’s Law is that what can go wrong will go wrong. We have investigated Murphy’s Law of:
- Buttered toast
- Supermarket queues
- Lifts
- Keys in pockets
- Traffic Lights
Home Activity
A simple example of Murphy’s Law operating in sport is some captains’ total inability to win the coin toss.
At home this week you are to try as hard as you can to emulate the feat of a certain New Zealand cricket captain by losing the toss four times in a row. Investigate with your child;
- How easy is this to do?
- Experiment to find out.
- Write down the results of your experiment and write a statement about how easy it is to lose the toss four times in a row.
Discuss together how Murphy's Law operated for you.