This unit develops an understanding of multiplication and division, including the inverse relationship between the two operations, and when and how to use them in problem solving situations. Students learn the conventions of how multiplication and division operations are represented as equations.
- Read, write and understand the multiplication and division symbols and the equals sign, and the language associated with these symbols.
- Write story contexts for given multiplication and division equations.
- Recognise that the operation of multiplication is commutative.
- Identify related multiplication and division facts ("families of facts").
- Recognise the inverse relationship of the operations of multiplication and division.
- Recognise that division is not commutative.
- Use the words ‘factor’ and ‘product’ appropriately.
- Identify the factors of given amounts.
This sequence of lessons makes the connection between repeated addition and multiplication. It introduces division and explores the relationship between the operations of multiplication and division.
There are three main understandings being developed within these lessons.
- Students need to understand the relationships among quantities that are represented by multiplication and division equations. For example, 4 x 5 = 20 might represent “four quantities of five are the same quantity as 20” or “20 is four times greater than 5.”
- Students need to learn the vocabulary associated with multiplication and division, and the meaning of those words. Important vocabulary includes factors (numbers being multiplied), product (answer to multiplication), multiplied by (making one quantity x times greater), equality (sameness of quantity).
- Multiplication can also be represented spatially. Arrays are a powerful way of showing the structure and pattern of multiple groups, and, in this case, strongly linking multiplication and division to measurement.
In exploring the structure and pattern of multiplication and division, the focus is also on developing an early understanding of number properties. The commutative property of multiplication (i.e. the order in which numnbers are multiplied does not change the answer) is formally explored in these lessons. The distributive property, in which one or both factors are partitioned to make calculations easier, (eg. 12 x 55 = 10 x 55 + 2 x 55), is foundational to calculation strategies, including written algorithms.
In exploring the behaviour of multiplication and division operations, it is important that students make generalisations in which they can state ‘what always happens’ when certain actions are undertaken. For example, they should recognise that whilst the ‘turn around’ rule (commutative) is always true for multiplication, it is not true for division.
This series of lessons focuses on single digit factors and divisors. It recognises that students must have many opportunities to represent multiplication and division. operations for solving word problems. This is underpinned by a strong understanding of using multiplication and division symbols and expressions to think mathematically, and to express relationships. Students also need to be able to create contexts that an equation might express. Making the connections between language and symbols is essential to developing a sound understanding of mathematical ideas and concepts.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- providing physical materials so that students can anticipate actions and justify their solutions. Using materials like cubes, square tiles, and array diagrams to model situations and connect strategies used by the students to the quantities that are represented.
- connecting symbols and mathematical vocabulary, especially the symbols for multiplication and division (x, ÷) and for equality (=). Explicitly modeling the correct use of equations and algorithms and discuss the meaning of the symbols in context.
- altering the complexity of the numbers that are used. Multiplication with factors such as two, four, five, ten, and division with the same divisors, tend to be easier than factors such as three, six, seven, eight and nine. Consider which multiplication facts your students will be confident in applying to problem solving.
- encouraging students to collaborate in small groups and to share, and justify, their ideas.
- using technology, especially calculators, in predictive, pattern-based ways to estimate products and quotients, e.g. If the answer to 4 x 8 = 32, will the answer to 32 ÷ 5 by more or less than 8? How do you know? Allowing the use of calculators where you want students to focus more on the process of getting a reasonable answer, or on noticing patterns, than on practising calculation skills.
The context used for this unit are quilts, tivaevae, and tapa cloth. Consider how you can incorporate community knowledge in this context. Are there community members who you could invite in to talk about the cultural background of tivaevae or tapa? In these contexts, it is important to ensure the authenticity, relevancy, and purpose of important cultural knowledge. You may wish to change the contexts to situations more relevant to your students’ everyday lives, interests, or cultural identities. Arrays are common across cultures and can be found in tiling patterns, textiles, packaging arrangements, piles for houses, and playing boards for games. Encourage students to be creative by accepting a variety of strategies from others and asking students to create their own problems for others to solve, in contexts that are meaningful.
- At least two rectangular quilts, tivaevae, or tapa cloth
- Coloured plastic square tiles (or small squares of different coloured card)
- Squared paper
- Calculators
- Unifix cubes
- Playing cards
- PowerPoint 1
- PowerPoint 2
- Copymaster 1
- Copymaster 2
- Copymaster 3
Session 1
Activity 1
- Show the students two different rectangular patchwork quilts. This would be a good opportunity to look at any school tapa cloths or tukutuku panels. Alternatively, use PowerPoint 1 to show pictures of suitable quilts or tapa cloth. For example:


Develop a context to frame the learning for this unit. This could include making a quilt or tapa cloth (even hypothetically) for the children’s ward at the local hospital or hospice. Consider how you can draw on the knowledge of your students and their community. Could adults bring in tivaevae, siapo, or quilts they have made, or photos of the items?
Engage students in a quilt discussion, establishing how the designs are created. - Ask, “ What mathematics is there in these quilts?” (eg. the 3 x 3 quilt)
Record the students’ ideas on the class chart. (These may include number, geometry, measurement statements: for example, 3 + 3 + 3 = 9, 3 x 3 = 9, 9 squares, one big square, sides the same length, 9 divided by 3 etc.). Compare the number of squares in different examples. - Highlight the operation and relationship symbols (or words) that have been recorded. For example:
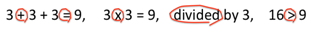
- Write each symbol on a separate A4 sheet of paper. Ask student pairs to take one sheet (one symbol) and each take turns to record, in a given time period (e.g. in 2 minutes), using words and pictures/diagrams, and brainstorm of all they know about this symbol (or word). Ask students to give an example of where their symbol might be used.
- Ask students to return to the mat, sitting in separate two groups: a group with operation symbols (+ - x ÷) and a group with relationship symbols (< > =). Have selected student pairs explain why they are sitting where they are, and what ideas they have recorded for their symbols.
In this discussion, emphasise the language used, develop the understanding of what a number operation is (a mathematical process that changes a number or an amount), and review the meaning of the equals sign.
Keep the brainstorm sheets for future reference.
Activity 2
- Prepare bags of 12, 18, 20, 24, and 30 plastic tiles, small coloured small squares of card, or fabric squares. Make these, pencils and paper, available to student pairs.

Pose the problem. “Show, using diagrams and equations, how many different ways can you arrange these patches to make a ‘mini patchwork quilt’?”
Have students work in pairs to record their ideas. - Have students share their ideas with a pair who had the same number of tiles, and record any arrangements they had not thought of.
- As a class, share ideas, exploring and recording key understandings on the class chart. Keep this student work for Session 2.
For example: From the bag of 18 ‘patches’ (tiles).
In the discussion, build on ideas shared in Activity 1 (above), highlighting and recording in words, these ideas:- The ‘patch’ arrangements can be recorded using different operations.
- Multiplication, using the x symbol, can show the same idea as repeated addition (of equal amounts), using the + symbol.
- The symbol for division, or sharing into equal groups, is ÷. It’s called the division symbol.
- This arrangement with equal rows and columns is called an array.
- Pose and record: “ 9 + 9 = 6 x 3. Do you agree or disagree.” Ask student pairs to discuss this claim and justify their position (explain why they agree or disagree, and how they know that they are right).
Record student justification, highlighting the relationship of equivalence (both are equal to 18, there are 18 patches altogether in both arrays). Highlight multiplicative views such as "9 equals 3 x 3 so 9 + 9 equals 6 x 3".
Activity 3
Write two equations on the class chart, one multiplication and one division.
For example: 6 x 5 = 30 28 ÷ 4 = 7. Read them together.Have each student draw a diagram of a quilt or tapa cloth that represents the equation. Ask them to write a description in words of how the quilt/cloth represents the equation.
Activity 4
Conclude the session by reviewing the operation and relationship symbols and their meanings.
Session 2
Activity 1
- Begin by having at least two students share their quilt/cloth diagrams from the previous session. Ask the other students to record equations that are represented in the diagram. Highlight the fact that real life maths can be represented using diagrams, words and symbols.
- Brainstorm on a class chart other situations in our lives where we see and use multiplication or division. As students share ideas, require them to suggest specific numbers. Record these stories using diagrams, and words.
For example: We see multiplication when:- 12 packets of 20 jellybeans are wrapped together in a bigger pack to be sold at the school fair – four packets in a row and three rows.
- The school buys three sets of hockey sticks with ten pieces in each set.
- At the marae, we sit in four rows of six.
- Read the stories again together. Ask students to use symbols to record the equations for each of the stories in their books/on whiteboard/paper. Those students who finish quickly can develop more context stories. Encourage students to develop context stories that reflect their daily lives (as opposed to selecting "random" numbers).
Have students pair share their equations. If students have recorded using repeated addition, have them also record multiplication equations.
Activity 2
- Review symbol information from Session 1, highlighting the operation symbols, + - x ÷ , and the relationship symbols, equals (=), greater than (>) and less than (<) relationship symbols.
Ask students to work in pairs using the situations from the previous activity. Students should discuss the situations, and see how many equations, or inequations they can write. For example:
3 x 4 = 4 x 3
3 x 4 < 2 x 10
4 x 6 > 2 x 10 > 4 x 3
They should use diagrams to show how they know that they are correct. - Have students pair share their work. As they do, they should take turns to read aloud what they have written.
Activity 3
- Return to the quilts/tapa cloth (pictures). Explain that some young children like alphabet quilts in which each patch shows a picture of something starting with a different letter of the alphabet. Talk about what some of these might be. For example: A might show an apple, B a butterfly, C a cat and so on.


- Make paper, pencils and felt pens available to the students.
Pose the problem: You are going to make an alphabet quilt/tapa cloth to gift to someone. You have till the end of the session today to plan your design and how you will arrange your 'square patches’. There might be a challenge somewhere in the problem. You decide the best way to solve this for your quilt design.
How many letters are in the alphabet? (26)
Why might making a quilt with 26 squares be a problem? - Let students experiment with 26 squares. They might draw the possible arrangements of use square tiles or cubes. Digital tools could also be used to organise the tiles, and present the students' creations.
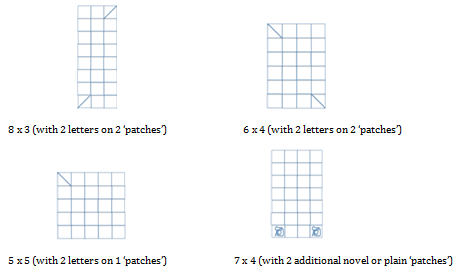
(26 will only make 1 x 26 or 2 x 13 arrays, which is undesirable for a quilt of this kind. Students will encounter ‘a remainder’ (6 x 4 + 2, 5 x 5 + 1) or they’ll find they are some ‘patches’ short (7 x 4). Accept realistic solutions for the context. (e.g. 5 x 5 quilt: put 2 letters on one patch, 6 x 4 quilt: make it 7 x 4 and include 2 novel or blank patches.) - Suggest: If we add patches for each of the digits 0-9, how many patches will we have then? (26 + 10 = 36)
See what quilts you could make then.
Look for students to find all the possible arrangements:
1 x 36 2 x 18 3 x 12 4 x 9 6 x 6
Which array is the best quilt/tapa cloth? Why?
Session 3
Activity 1
- Have students share their alphabet quilt designs for 36 patches.Discuss the ‘remainder issue’ and commend creative solutions.
Why was a quilt with five patches in a row not possible?
Record 36 ÷5 = 7 r 1 and ask students what r 1 means (remainder of 1).
Point out that often division problems don’t work out evenly. We call what is left over, a remainder. - Imagine we had 26 patches and tried to put six patches in each row. One way we could record this problem is 26 ÷ 6 = 4 r2.
- On the class chart quickly draw the arrays that were developed for 26 patches.
- Discuss the ‘dimensions’ of the array, introducing the words factors and product. Model with an example:

Have each student record below their quilt designs, what is in the box above, adjusting the numbers for their own design.
Activity 2
- Write 4 36 9 on the board.
Here are three other numbers that are connected by multiplication and division.
Record a set of multiplication and division equations using these numbers. - Have students work in pairs to develop equations, and to create an array that represents all four equations. Students must be prepared to justify their position (explaining how they know they are right).
4 x 9 = 36 9 x 4 = 36 36 ÷ 4 = 9 36 ÷ 9 = 4
Relate each equation to the 9 x 4 array which students should recognise from the previous quilt design activity. Pay particular attention to division. For example, 36 ÷ 4 = 9 gives the number of rows created from 36 patches (the area) if each row is made from four patches. - Summarise findings on a class chart. For example:
- There are four related facts only (family of facts) and no more.
4 x 7 = 28 7 x 4 = 28 28 ÷ 4 = 7 28 ÷ 7 = 4 - Multiplication is a ‘turn around’ operation. You can change the order of the factors without changing the product. (It’s like addition.)
We say that multiplication (and addition) are commutative.
4 x 7 = 7 x 4 = 28 - Division isn’t commutative, e.g. 36 ÷ 4 = 9 but 4 ÷ 36 = 0.1111… (1/9). The divisions do not have the same quotient (answer).
We say that division (and subtraction) are not commutative.
- There are four related facts only (family of facts) and no more.
Activity 3
- Ask students to play the game Multiply, Draw and Write in pairs. Consider pairing students together who have similar levels of times table knowledge, thus encouraging tuakana-teina and students' confidence in their own skills.
They need playing cards (with numbers 2 to 9), pencil and paper.
The winner is the person who, after ten rounds, has the most pairs of cards with products that are the same, but which are made with different factors.
For example: 6 x 4 = 8 x 3 = 24, or 4 x 4 = 2 x 8 = 16
How to play:
The cards are shuffled and placed face down in a pile between both players.
Players take turns to turn over three cards from the pile. These are the factors. The player returns one card to the bottom of the pile. The player must write the multiplication fact/s for the two cards. They might also draw an array and write the family of facts.
For example: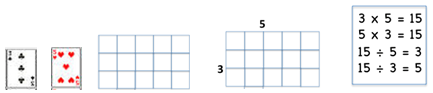
- Students conclude the session by writing word scenarios for their equation sets (family of facts). You might choose to work with students, who would benefit from more support, in a small group whilst other students work independently. Ultimately, all students should be able to write word scenarios for the equation sets. These could be written using digital tools, and could be modelled with the use of materials (e.g. counters). These do not have to be quilt scenarios.
For example: “There were three bags with five apples in each. Fifteen shared among three bags is five. If these fifteen apples were put into five bags, there would be three in each. That would be five lots of three.”
Session 4
Activity 1
Show an alternative quilt or tapa cloth array (PowerPoint 2). For example:
Have four students record one of each of the related facts.
(6 x 5 = 30, 5 x 6 = 30, 30 ÷ 5 = 6, 30 ÷ 6 = 5) and explain each fact with reference to the quilt, including demonstrating the commutative (turn around) property of multiplication. Turn the quilt to demonstrate this.
Activity 2
- Make linking cubes (or coloured counters) available to the students. Have pairs of students each take 48 cubes. Ask what factors could make 48. Record possibilities using multiplication; 1 x 48, 2 x 24, 3 x 16, etc.
- Have one student of each student pair model 4 x 12, linking the cubes. Then have their partner use the same cubes to model 12 x 4. Discuss what happens. (They needed to regroup these). Repeat with 6 x 8 and 8 x 6. Emphasise that the commutative property involves the same factors and product, but requires a different way to look at the array(i.e. either the rows or the column form the equal sets).
- Put the multiplication facts for 48 onto cards (Copymaster 1). Hold back 5 x ? and 7 x ? Match up the pairs of equations that show the commutative property.
Do you think this is all the multiplication facts with a product of 48? (You could arrange the cards by order of the first factor.)
Why are there no 5 x and 7 x facts? (Use the cards. Students should realise that 48 is not in the set of multiples of 5 and 7. 48 is not divisible by 5 and 7).
Use a calculator to show that 48 ÷ 5 = 9.6 and 48 ÷ 7 = 6.857142857…
What do you think the decimal part of the product shows? (A remainder so 48 is not divisible by 5 and 7) - Ask students to explore multiplication facts with a different number of cubes, using the language of same factors and product, focusing on regrouping. Their investigation might show that some numbers only have two factors, such as 17 and 31. These numbers are primes.
Activity 3
- Record one familiar multiplication equation on the class chart. For example, 6 x 2 = 12. Have one of the students in each pair model this, by making 6 groups of 2 and linking the cubes together into one line of 12.
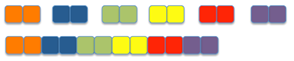
Record 12 ÷ 6 = 2. Have the other student in the pair enact this with the cubes.
Have students describe what has happened and record ideas such as: it’s the opposite, division undid multiplication, it’s the reverse, we’re back where we started.
Ask, Is this always true? How can we find out? Accept student ideas. These should include the students exploring more examples. - Conclude that it is impossible to try all multiplication and division facts. Say that the ‘undoing’ idea means that multiplication and division are inverse operations, just like turning a light switch on and off. Undoing each other is just the way that multiplication and division behave.
- Write "inverse relationship" on the class chart. Discuss words similar to inverse e.g. reverse, undo, put back, return, and their meaning. Make the connection to the inverse relationship between addition and subtraction. Highlight that in each operation pair, one operation or action undoes the other.
- Return to the quilt in Activity 1 (above) and to the equations recorded:
(6 x 6 = 30, 5 x 6 = 30, 30 ÷ 5 = 6, 30 ÷ 6 = 5)
Ask students to explain the ‘undoing’ (the inverse relationship again, with reference to the quilt. (This is a little harder to see because this array cannot physically be ‘undone.’ However, you might create rows of six cubes and show 5 x 6 by arranging five rows vertically. How many patches do I have? What happens if I now divide by five?) - Write on the class chart:
Knowing that multiplication and division are inverse operations is helpful because……..
Have students suggest reasons and record these, including:
We can use multiplication to help us solve division problems.
We can check division operations using multiplication. (How?)
Activity 4
Distribute Copymaster 2 for students to work from. Emphasise the inverse operations, and the need for students to show or explain how multiplication helps to solve division problems.
Session 5
Activity 1
Review key learning from Session 4. Have students work in pairs to share their solutions to the quilt problems from Session 4, Activity 4. Encourage them to question each other.
Activity 2
- Display some quilt or tapa cloth examples using PowerPoint 1:



- Write on the class chart:
One quilt of sixteen patches:
One quilt of thirty patches:
One quilt of forty-five patches:
If I rearranged the patches into a single row, what would the quilt look like? (More like a long scarf) - Ask students to record multiplication equations for each of these statements.
One quilt of sixteen patches: 1 x 16 = 16
One quilt of nine patches: 1 x 30 = 30
One quilt of thirty patches: 1 x 45 = 45
If your equations are correct what are the answers to 16 ÷ 1 = ☐ , 30 ÷ 1 = ☐ , 45 ÷ 1 = ☐? - Ask students to discuss their ideas, then explain and justify their thinking. Do they relate the division to “How many columns of one patch make a total of 16, 30, or 45 patches?”
If your equations are correct what are the answers to 16 ÷ 16 = ☐ , 30 ÷ 30 = ☐ , 45 ÷ 45 = ☐?
Do they relate the division to “How many rows of 16 patches make a total of 16 patches, etc? - Pose other examples of dividing a number by one and itself. Calculators can be used to check answers.
Activity 3
Have students work in groups of 2 to 4 on Is it a fact? (Copymaster 3 (Purpose: To discriminate between correct and incorrect multiplication and division equations and expressions, and be able to explain why, justifying their decision)
Students take turns to choose a statement and explain to others in the group, if and why the statement is a fact, or if and why it is incorrect (true or false).
Ask students to create their own facts or non-facts that involve multiplication and division, e.g. 8 x 9 = 72 so 72 ÷ 18 = 4. Exchange the facts and non-facts among students.
Activity 4
Conclude this session by reviewing the learning that has happened over the five sessions.
Dear parents and whānau,
In algebra this week we have been learning about the number operations of multiplication and division and the relationship between them.
One way that students consolidate what they have been learning is to read true and false statements and to identify and explain which ones are incorrect and why.
Your child might like to play the "Is it a fact?" game with you. In taking turns, it is really important that each person explains why a statement is true or not.
We hope that you enjoy the challenge.
Thank you.
Try these examples:
1 x 25 = 25 so 25 ÷ 25 = 1 True or False
28 ÷ 4 = 7 so 4 ÷ 28 = 7 True or False