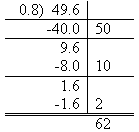In this unit we look at a range of strategies for solving multiplication and division problems with whole numbers and decimal fractions, with a view of students anticipating, from the structure of a problem, which strategies might be most suitable. This unit builds on the ideas presented in Multiplication and Division Pick ‘n’ Mix 1.
- Mentally solve whole number and decimal fraction multiplication and division problems using:
- proportional adjustment
- place value
- tidy numbers
- factorisation
- Use appropriate recording techniques.
- Predict the usefulness of strategies for given problems.
- Evaluate the effectiveness of selected strategies.
- Generalise the types of problems that are connected with particular strategies.
The strategy section of the New Zealand Number Framework consists of a sequence of global stages that students use to solve mental number problems. Within this framework, students working at different strategy stages use characteristic strategies to solve problems. This unit is useful for students working at Stage 8 - Advanced Proportional of the Number Framework. Students at this stage select from a broad range of strategies to estimate and solve multiplication and division problems involving decimal fractions. The Number Framework also includes a knowledge component which details the knowledge students will need to develop in order to progress through the strategy stages of the framework. This unit draws on students' knowledge of multiplication and related division facts to 10, compatible decimal fractions to 1 (along with whole number compatibility) and place value relationships to 3 decimal places.
The key teaching points in this unit are:
- Some problems are easier to solve in certain ways. Teachers should elicit strategy discussion around problems in order to get students to justify their decisions about strategy selection in terms of the usefulness of the strategy for the problem situation.
- Useful strategies for multiplication include place value partitioning, rounding and compensating, proportional adjustment and factorisation.
- Useful strategies for division include proportional adjustment (with factorisation), rounding and compensating, and partitioning or ‘chunking’.
- Tidy number strategies (rounding and compensating) are useful when number(s) in an equation are close to an easier number to work from.
- When applying tidy numbers in multiplication and division it is important to keep track of what has been changed in a problem in order to compensate (rounding and compensating)
- Place value strategies are most useful when little or no renaming is needed.
- Proportional adjustment is useful when there is a connection between the numbers that can be used to simplify the problem such as doubling and halving or quadrupling and quartering. Division with factorisation can be viewed as a form of proportional reasoning. In division both of the numbers must be reduced by the same factor.
- Factorisation is useful for multiplication when one of the factors can be reduced.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- using place value-based materials alongside symbols to develop both understanding and fluency with calculation methods
- encouraging students to work in collaborative teams to develop explanation and justification strategies
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities
- varying the size and complexity of numbers in the problems to cater for a range of proficiencies.
The contexts presented in this unit revolve around distance and quantities. Other situations of relevance to your students might be used to capitalise on contextual knowledge and increase motivation. For example, amounts of money, number of people or items, distance to relevant places. Consider what contexts will make links to your students' cultural backgrounds, interests, and to their learning from other curriculum areas.
Te reo Māori kupu such as whakarea (multiply, multiplication), whakawehe (divide, division), hautanga ā-ira (decimal fraction), tauoti (whole number), uara tū (place value), tau māmā (tidy number), and tauwehe (factor) could be introduced in this unit and used throughout other mathematical learning.
You could also encourage students, who speak a language other than English at home, to share the words related to multiplication and division used in their home languages.
- Decimal place value equipment (e.g. decimats)
Getting Started
The purpose of this session is to explore the range of strategies that students have to solve multiplication and division problems. This will enable you to elicit the strategies that students currently use and evaluate which strategies need to be focused on in greater depth as well as identifying students in your group as "expert" in particular strategies. Consider adapting the contexts reflected in the problems presented to better relate to the cultural backgrounds, interests, and learning from other curriculum areas that are relevant to your students.
After posing each problem, provide time for students to work out the answer. Encourage them to work out the answers mentally. If the use of materials is necessary for students, encourage them to work towards imaging and folding back to materials (as opposed to only relying on materials). Provide calculators for students to use as a way to check their calculations. Ask students to share their solutions and strategies with a partner. Alternatively, you might group students who have used the same strategy, and have them share their work together, before sharing with the class.
As a class, discuss the strategies used. As different strategies arise ask the students to explain why they chose to solve the problem in that way. Have them model the strategy for the class. Accept all the strategies that are elicited at this stage, recording them to reflect upon later in the unit (perhaps in a modelling book or on a class chart).
Students who solve these problems quickly could be challenged to prove their solution with other strategies, or could be asked to make up similar problems.
Problem 1:
Shawna swims 0.5 kilometres each day for 28 days. How many kilometres has she travelled by the end of the five days?
Rounding and Compensating:
28 x 0.5
28 is rounded to 30, so the equation becomes 30 x 0.5 (15). Then 2 x 0.5 (1) must be removed to complete the equation.
Proportional adjustment:
28 x 0.5
Solve instead 14 x 1 - doubling and halving
Place value partitioning:
28 x 0.5
Solve (20 x 0.5) + (8 x 0.5).
Problem 2:
Ruataniwha House are selling bags of nuts for a fundraiser. They buy a sack of nuts weighing 27kg, and repackage the nuts into 0.45 kg bags for sale. How many bags will come from the sack? (27 kg ÷ 0.45 kg)
Place Value Partitioning (Chunking):
27 ÷ 0.45
10 bags would make 4.5 kg, so 20 bags would make 9 kg. 3 lots of 9 is 27… they can make 60 bags.
Proportional adjustment:
If I double both sides I get 54 ÷ 0.9. 54 ÷ 9 is 6, so 54 ÷ 0.9 must be 60.
Ask students to reflect on the strategies that have been discussed in the session and evaluate which strategies that they personally need further work on, perhaps using thumb signals - thumbs up - confident and competent with the strategy, thumbs sideways - semi confident, and thumbs down - not yet confident. Use this information to plan for your subsequent teaching, using ideas from the exploring section outlined below.
Exploring
Over the next two to three days, explore the following strategies, making explicit the strategy you are concentrating on and your reason for doing so.
e.g. In the problem 2.9 x 7, rounding and compensating would be a useful strategy to use because 2.9 is close to 3.
Each day follow a similar lesson structure to the introductory session, with students sharing their solutions to the initial questions and discussing why these questions lend themselves to the strategy being explicitly taught. Conclude each session by having students make some statements about when this strategy would be useful and why (e.g. "place value is useful when there is limited renaming required" or "factorisation is useful when one of the factors is able to be renamed as a series of smaller factors"). It is important to record these key ideas as they will be used for reflection at the end of the unit.
The following questions are provided as examples for the promotion of the identified strategies. If the students are not secure with a strategy you may need provide extended opportunities for practise, using your own questions, to address student needs.
Consider providing a means for all students to record their thinking, from throughout the unit, in a structured way (e.g. a Think Mat, graphic organiser, mind map, booklet).
If necessary, use and provide materials to model problems and support students' thinking.
Rounding and compensating (Multiplication)
Bozo the Clown fires 4.8 L of water from his water pistol each night at the circus. How many litres does he fire over two weeks?
The tidy numbers strategy involves rounding a number in a question to make it easier to solve. In the above question 4.8 can be rounded to 5 (by adding 0.2). The problem then becomes 5 x 14. The 14 groups of 0.2 L added to ‘tidy’ the problem now need to be subtracted, leaving a total of 67.2 L.
The following questions can be used to elicit discussion about the strategy:
- What tidy number could you use that is close to one of the numbers in the problem?
- What do you need to do if you tidy up this number? Why?
- Why is this strategy useful for this problem?
- What knowledge helps you to solve a problem like this?
Place value equipment can be also be used to show the problems physically.
Further questions for practice:
6.9 x 9
1.48 x 7
13.98 x 6
12.96 x 32
7 x 9.998
5.48 x 3
Note that the problems posed here are using a tidying up strategy rather than tidying down. If one of the factors is just over a tidy number (such as 203) then place value tends to be a more useful strategy.
Rounding and compensating (Division)
Ohau House uses 0.7L of detergent every time they do a fundraising car wash. They have 13.3L of detergent left… for how many car washes will it last?
Rounding and compensating for division involves finding a number that is close to the total, and working from that number to find an answer. For the question above, a student might say:
I know that 0 .7 times 20 would be 14. 13.3 is 0.7 less than 14, so the detergent would last 19 car washes.
The following questions can be used to elicit discussion about the strategy:
- What tidy number could you use that is close to one of the numbers in the problem?
- What do you need to do if you tidy to this number?
- Why is this strategy useful for this problem?
- What knowledge helps you to solve a problem like this?
Further questions for practice:
34.3 ÷ 7
19.8 ÷ 9
119.4 ÷ 6
13.3 ÷ 0.7
1683 ÷ 1.7
Proportional Adjustment (Multiplication)
Bob the bodybuilder adds 2.5 kg to his weightlifting bar each day. How much will he have added after 32 days?
Proportional adjustment involves using knowledge of multiples to create equivalent equations. Factors are proportionally adjusted to make one (or both) factors easier to work from. In the above problem the factors could be adjusted as follows: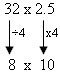
Alternatively, students might double the 2.5 to 5, and halve 32 to 16.
The following questions can be used to elicit discussion about the strategy:
- What could you multiply one of these numbers by to make it easier to work with?
- What would you then need to do to the other number?
- Why is this strategy useful for this problem?
- What knowledge helps you to solve a problem like this?
Further questions for practice:
3.33 x 18 (thirding and trebling)
60 x 7.5
300 x 1.8 (thirding and trebling)
120 x 2.25
24 x 1.25
Proportional Adjustment (Division)
Jonno has 168m of rope to cut into 1.2m lengths. How many bits of rope can he make?
In division proportional adjustment involves reducing or increasing both numbers in the equation by the same number. Therefore, the numbers used to proportionally adjust the problem must be factors of both numbers in the equation. For example,
If I divide the 168 and the 1.2 by 2 my equation becomes 84 ÷ 0 .6 and I can divide them both by 2 again to get 42 ÷ 0 .3 which is 140 or I could divide them both by 4 to get the same equation.
The following questions can be used to elicit discussion about the strategy:
- What could you divide both of these numbers by to make an easier equation?
- Why is this strategy useful for this problem?
- What knowledge helps you to solve a problem like this?
Further questions for practice:
180 ÷ 1.5 (→ 360 ÷ 3)
367.5 ÷ 3.5 (→ 735 ÷ 7)
196.2 ÷ 18 (→ 98.1 ÷ 9)
1498 ÷ 1.4 (→ 749 ÷ .7)
172.8 ÷ 16 (→ 86.4 ÷ 8)
Place Value Partitioning (Multiplication)
Mae Ling uses 3.12m to make a traditional dance outfit. How much fabric will she use to make 8 outfits?
The place value strategy involves multiplying in place value (e.g. ones, tenths and hundredths). In the above problem the student might say the following:
I multiplied 3 x 8 and got 24. Then I added the 0.8 (0.1 x 8) and 0.16 (0.02 x 8) to get 24 .96 m
The following questions can be used to elicit discussion about the strategy:
- How can you use your knowledge of place value to solve this problem?
- Why is this strategy useful for this problem?
Further questions for practice:
613.23 x 30
7 x 4.1112
10.21 x 40
354 x 0.11
An extension of the place value strategy involves the use of standard written form for multiplication.
Place value partitioning (division)
Sheila mixes 0.8kg of milk powder with water each time she feeds the calves. If there is 49.6kg left in the bag, for how many feeds will the milk powder last?
The place value partitioning strategy for division involves ‘chunking’ known facts and subtracting them from the answer. The long division written form will be familiar to most teachers. In the case above, a student might think:
Ok, 10 lots would be 8kg. That means 50 lots would be 40kg. That leaves me with 9.6 kg. So if I take off another 10 lots that’s another 8kg. That leaves me with 16 kg left over, or 2 lots. So the answer is 50, plus 10, plus 2… 62 feeds!
This thinking could be recorded as:
The following questions can be used to elicit discussion about the strategy:
- How can you use your knowledge of place value to solve this problem?
- Why is this strategy useful for this problem?
Further questions for practice:
67.6 ÷ 0.4
97.6 ÷ 0.8
380.8 ÷ 0.7
472 ÷ 1.5
546 ÷ 1.8
An extension of the place value strategy involves the use of standard written form for division.
Factorisation (multiplication and division)
Maree is putting up a 148.8m long fence. She places a post every 8m. How many posts does she need?
The factorisation strategy involves using factors to simplify the problem. In this instance eight can be factorised as 2 x 2 x 2. This means dividing by two, then two, then two has the same net effect as dividing by 8. Likewise, multiplying by two, then two, then two has the same net effect as multiplying by 8. In applying factorisation to the above problem, a student might think:
Dividing by 8 is the same as dividing by 2, then 2, then 2. So, 148.8 ÷ 2 = 74.4. Then 74.4 ÷ 2 = 37.2. And last, 37.2 ÷ 2 = 18.6. The answer is 18.6m.
The following questions can be used to elicit discussion about the strategy:
- How can you use your knowledge of factors to solve this problem?
- Why is this strategy useful for this problem?
Further questions for practice:
53.2 ÷ 8 (÷2, ÷2, ÷2)
3.48 ÷ 12 (÷2, ÷2, ÷3)
43.2 ÷ 27 (÷3, ÷3, ÷3)
1.35 x 12 (x2, x2, x3)
4.3 x 8 (x2, x2, x2)
2.7 x 16 (x2, x2, x2, x2)
Reflecting
To conclude the week's work, give the students the following five problems to solve asking them to predict which strategy they think will be useful for each problem and why they think this is the most efficient strategy before they solve them. After they have solved the problems engage in discussion about the effectiveness of their selected strategies for the problems. It is fine if students do not agree with the group about the usefulness of a particular strategy in a given problem. Encourage them to justify their thinking and model the use of their preferred strategy.
Problems for discussion (more than one strategy might be suitable for these)
68 x 3.5 (proportional adjustment)
46.2 ÷ 1.4 (place value partitioning)
2.93 x 6 (rounding and compensating)
169.5 ÷ 1.5 (proportional adjustment)
23.2 x 11 (place value partitioning)
7.04 ÷ 8 (factorisation)
161.7 ÷ 1.63 (rounding and compensating)
4.11 x 16 (factorisation)
Ask the students to create problems for a partner where one of the strategies covered in this unit is the most useful.
Conclude the unit by showing the students the questions asked in the initial session again. Have students discuss whether they would solve them in a different way now, and explain why. Review the modelling book/chart or record of statements or generalisations about the strategies and make any changes.
Dear families and whānau,
We have been exploring a range of strategies that can be used to solve multiplication and division problems with whole numbers and decimal fractions. As part of this, we have been working on finding the most suitable strategy for a given problem. Some of these strategies might be quite different to ones you are familiar with!
Create a multiplication or division problem, and ask your child to teach you a strategy that could be used to solve it. You might also teach your child a strategy that you are familiar with.