Motorcycle Mayhem

Activity One

Financial understanding
In this activity, Daniel realises that having a goal will help him to save the money he needs to buy the motorbike he wants.
Students will benefit from doing pages 8–9 before they start this activity because those pages give an introduction to bank statements. Alternatively, you could begin with a general discussion on bank statements (see the notes for pages 8–9), especially to clarify new terms such as those above and their abbreviations.
Showing students some real bank statements is also useful.
Have your students look at the bank statement on page 12. Some questions you could ask to cue students into the features of this statement include:
What are the opening and closing dates for this bank statement? (31 March and 30 May. Note this doesn’t mean the account itself was opened and closed on these days.)
What will be the dates on Daniel’s next bank statement? (Opening 31 May and closing 31 July)
How much and how often is Daniel charged a bank fee? ($2.50 monthly)
Why do you think Daniel is charged a bank fee? (The bank is providing a service in handling Daniel’s money. The bank fee is the cost of this service.)
How much money has Daniel saved during these 2 months? (4 x $200 = $800)
After discussion, your students should be able to complete Activity One independently, in collaborative groups, or with you.

Activity Two

Financial understanding
In this activity, Daniel has researched a number of different deals to help him make a more responsible financial decision. His decision will depend on the preferences he has and the criteria he sets.
Mathematics and statistics
For question 1, the students need to compare the closing balance with the prices. Question 2 can be tackled either as it is described in the Answers section (which requires students to be at least at stage 7) or more simply if students use rounding to estimate the answer. Rounding $2,856.10 to $2,900 is appropriate in this context.
(You may wish to have some discussion on the subject of choosing the appropriate accuracy for rounding.
Rounding to the nearest 100 is sensible because the savings are added $200 at a time. If the savings were less than $100, then rounding to the nearest 10 would make more sense.) The students will need to reconsider this rounding when applying the answer to the problem because it could mean Daniel would be at least $43 short of
the full amount due to the rounding error.
Students who are at stage 6 may approach this task by adding $200 to $2,900 repeatedly (doing this 30 times gives $8,900, which is enough to buy the Wild Cat RV250). A more sophisticated strategy is to subtract $2,900 from $8,900 and divide by 200; $6,000 ÷ $200 = 30, that is, 30 fortnights, which is approximately 14 months.
However, because the current amount in Daniel’s account was rounded up to $2,900, he will need one more pay to cover the cost, that is, 31 fortnights or 14 months.
Students who calculate the answer without rounding first (that is, $8,900 – $2,856.10 = $6,043.90; $6,043.90 ÷ $200 = 30.22 [fortnights]) will still need to round their answer to make sense of it in the context of the problem. Daniel wouldn’t receive 0.22 of a fortnight’s pay, so the answer must be rounded up to 31 pay
periods (fortnights).
Extension
As an extension, the students could work out how long it would take to save for the other two bikes.
Note: Students may have difficulty in problem solving that uses weeks, months, and years. A common error is to consider 1 month = 4 weeks. In fact, 11 out of the 12 months in a year are slightly more than 4 weeks;
52 (weeks in a year) ÷ 4 = 13, but there are only 12 months in a year.
Financial understanding
Buying vehicles is a very appropriate context in which to look at insurance. The same types of insurance for cars are:
• Full insurance covers any costs if the bike is involved in an accident – no matter whose fault it is. It also covers the value of the bike if it is stolen or the cost of repairs if it is damaged in a way covered by the policy conditions.
• Third party insurance covers the cost of damage to another vehicle if it is involved in an accident that was the bike driver’s fault, but it doesn’t cover repairs to the bike itself.
• Fire and theft insurance will pay the value of the bike only if it is destroyed in a fire or stolen.
All of these types of insurance also involve an excess. This is the amount the owner has to pay before the insurance company will cover the rest. (The amount of excess will vary, depending on factors such as the type of bike and the age of the owner.)
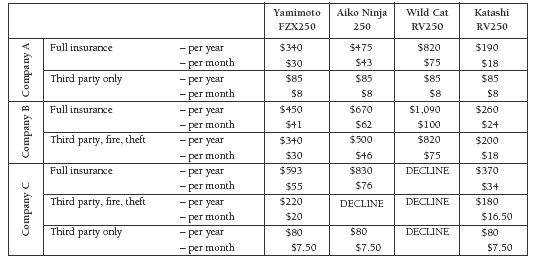
The following table provides insurance quotes from three companies for the above types of insurance for each of the different bikes Daniel is choosing from.

Possible questions:
Which type of insurance is the most expensive – full, third party, fire and theft, or third party only? (Full)
Which bike is the most expensive to insure? (The Wild Cat RV250)
Which company offers the best deals for full insurance? (Company A is the cheapest for every bike.)
Why do you think company A doesn’t quote for insuring the bikes for fire and theft? (Possibly because motorbikes are comparatively easy to steal and therefore not worth the risk)
Why do you think company C won’t insure the Wild Cat RV250 bike? (Possibly because the Wild Cat RV250 is expensive, which implies that it would be more desirable to steal, or it may be faster than the others, making it more likely to be involved in a crash. Either situation means the risk for the insurer is too great.)
If Daniel wanted to insure a Katashi RV250 bike against theft only, which insurance company should he use? (Company C; their quote of $180 is cheaper than Company B’s quote of $200 [both also include third party and fire] or Company A’s full cover of $190. Although for an additional $10 a year, he might be wise to look at full cover.)
If Daniel decides to buy the Yamimoto FZX250 bike and take out full insurance, which company should he choose?
(Probably company A; it is the cheapest at $340 per year. However, he should also find out how much excess each company would require him to pay if he made a claim. Company A might have lower rates because it has a high excess.)
The students could also consider the reputation of various insurance companies. This is a factor that often influences our decision making.

Social Sciences Links
Achievement objectives:
• Understand how people make decisions about access to and use of resources (Social Studies, level 3)
Ask Why do you think Daniel initially decides to save his money and not “access” it?
• Understand how producers and consumers exercise their rights and meet their responsibilities (Social Studies, level 4)
Ask: Apart from price, what else could influence Daniel’s decision about what bike to purchase? What are some of Daniel’s rights as a consumer if he purchases one of these bikes?

Answers to Activities

Activity One
1. a. Every fortnight
b. $200
2. a. 1 May
b. About 5 months (based on his current savings pattern)
3. Approximately $2,856
Reflective question
Answers may vary. Daniel was thinking about the fact that he was spending all his income and some of that spending was unnecessary, with nothing to show for it. He was also thinking about the future: his goal is to buy a motorbike, but he can’t if he
keeps spending all the money he earns.
Activity Two
1. He only has enough money for the Katashi.
2. At $200 a fortnight, it would take him about another 14–15 months. ($8,900 – $2,856 = $6,044. $6,044 ÷ 200 = $30.22, which is 30 pays, without rounding. With rounding, it is 31 pays because you normally can’t have a part pay. 31 pays is 62 weeks, which is 14–15 months.)
3. Answers will vary, including insurance, repairs and maintenance, safety gear (for example, helmet), running costs (for example, petrol, oil).
Reflective questions
• No, because even if two people want the same item, they will have different ideas about how hard to save for it, different choices about how to earn the money, and so on.
• Their “spare” income, their current debts, their ability to look at financial options, other ways they want to spend their money, and so on, might influence their choices.