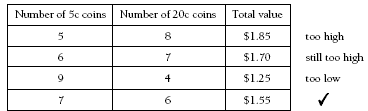These are level 3 geometry, and algebra problems from the Figure It Out series.
Click on the image to enlarge it. Click again to close. Download PDF (832 KB)
interpret three dimensional drawings (Problem 2)
use algebraic thinking to solve problems (Problem 3)
predict the results of paper folding reflections (Problem 4)
Problem One
The students can solve this problem by using trial and improvement and recording the results on a table that shows different combinations of 5 cent and 20 cent coins, always with a total of 13 coins.
Encourage the students to look for patterns that will improve the accuracy of their trials. They may notice that increasing the number of 5 cent coins by one and decreasing the number of 20 cent coins by one reduces that total by 15 cents. The original guess in the table above is too high. This means that you need to increase the number of 5 cent coins by two and decrease the number of 20 cent coins by two to reduce the total by 2 x 15c = 30c.
Here is another way to look at the problem:
The nearest multiple of 20 to 155 is 7 x 20 = 140. This means seven 20 cent coins, which is no good because you would then need six 5 cent coins to make the 13 coins. 6 x 5 = 30 and 140 + 30 = 170, which is too much. The next lowest multiple of 20 is 120, which is six 20 cent coins. You would then need seven 5 cent coins to make the 13 coins. 6 x 20 + 7 x 5 = 155, so six 20 cent coins and seven 5 cent coins = $1.55, the amount that Titus had.
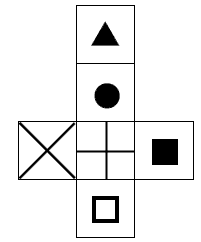
Problem Two
One way to think about this is to look at the first and the third drawings of the cube. Notice that these show all four of the sides that are next to the that is, the
The only shape that hasn’t been accounted for is the
so the
must be opposite the
.
Some students will find it very hard to visualise this. Give them blank cubes and let them draw the shapes on the faces. This does not mean that these students are necessarily poor at maths. There are a lot of bright people who have trouble visualising things like this.
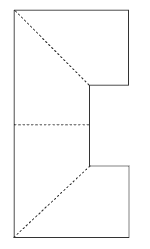
Making a model of the cube using the net shown in the Answers is a simple way of demonstrating this problem.
Problem Three
This problem can be solved very simply, as long as the students think carefully about the information they have been given.
Heinz needs 25 cents more to buy the ruler. If Phoebe gives Heinz the 25 cents he needs, she will have 30 cents left. (We are told that together they have enough money to buy a ruler and have 30 cents change.) So Phoebe initially had 30 + 25 = 55 cents. Heinz must have had 40 cents at the start because Phoebe started with 15 cents more than him (55 – 15 = 40 cents).
Problem Four
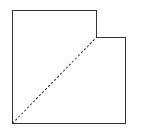
This problem can be solved by working backwards.
Start at the last picture. Going back one step will open up the cut triangle. This means that the cut piece will still be partly horizontal, but it will also be partly vertical. So at this stage, there is a small square cut out of the folded square shape.
If you unfold to go back another step, the cut-out square opens up to become a cut-out rectangle. Its horizontal sides are the same length as the original cut. Its vertical sides are twice this length.
As you unfold to get back to the original square, the cut-out rectangle folds out to make a square whose sides are the same length as the rectangle. So the hole is a square whose sides are twice as long as the original cut.
Extension
As in Problem Two, many students will have difficulty visualising what is going on. Give them paper and scissors and let them experiment with their cuts. “What happens if you cut off another corner?” Get them to guess and then do it. “What if you try a zigzag cut? What if you fold the paper some other way?” This will give the non-visualisers practice in visualising.
Hints for Students
1. You might use trial and improvement here. You can be more systematic if you use a table.
2. Try drawing a net diagram, which you can use for constructing a cube.
Now fill in the icons on each face of the net.
3. Sometimes it pays to work backwards through the list of clues. Try this.
4. Try to solve this problem in your head by doing it backwards.
If this is difficult, do the problem with a square of paper and scissors.
Answers to Problems
1. Six 20c coins and seven 5c coins
2.
A net of the cube could look like this:
3. 55c
4. A square