The Mirror Game

Game

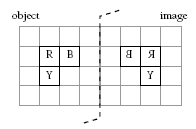
The mirror game is designed for students to apply reflection symmetry. Although Perspex mirrors are ideal because a matched cube can be seen to coincide with its reflection, backed mirrors are adequate for students to check that they have placed the matching cube correctly.
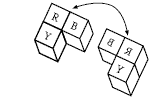
The harder version of the game, involving composite pieces, fosters discussion about the properties of reflections. For example, consider the case:Although the size and shape of the object remains unchanged, its orientation (direction) changes. This
orientation change is described as a “flip” in American mathematics books.

A flip is a useful way to describe the movement.

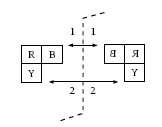
Note that the distance between any block and the mirror should be the
same as the distance between the image of the block and the mirror:

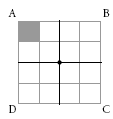
As an extension to this activity, students may like to play The Rotation Game. In this game, players match a cube that is put down with its image after a quarter turn. For this reason, people play on four grids.
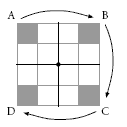
i. Player A places a cube:

ii. Players B, C, D, in succession, match where the cube would end up in their quadrant after each quarter turn:

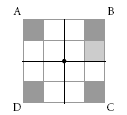
iii. Player B has a turn placing

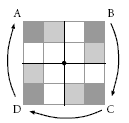
iv. Players C, D, and A take turns to a different cube in their quadrant. match where the cube would end up in their quadrant after each quarter rotation:

Students can check their attempts at placement by turning the paper a quarter turn and then back to its original position. The game is much more difficult if each player has a 3 x 3 quadrant, which makes the player’s total grid 12 centimetres x 12 centimetres, or a 4 x 4 quadrant grid, which is 16 centimetres x 16 centimetres in total.
As with The Mirror Game, students can take the cubes off one by one and colour the grid to record their pattern.