Make a Ten
This unit follows naturally from the Smart Doubling unit.
In this unit students are encouraged to further develop part/whole mental methods by using the strategy of "make a ten".
demonstrate automatic recall of all pairs of single digit addition facts whose total is 10 or less
use the mental strategy "make a ten" for addition problem
use the most efficient mental strategy for a given problem.
In this unit students are encouraged to add to their use of part/whole with doubles by using "make a ten" methods.
Examples of "part/whole" methods using make a ten:
The students work out 8 + 5 by removing 2 from the 5 to leave 3, add this 2 to the 8 to make 10 then add the 3 to the 10 to give 13.
The students work out 38 + 8 by removing 2 from the 8 to leave 6, add the 2 to the 38 to give 40, then add 6 to the 40 to give 46.
It is desirable for students to move to part/whole methods as counting methods fail for larger numbers. For example, a student who attempts to work out 36 + 46 by counting on will soon lose their way, whereas the part/whole thinker could solve this by adding 30 and 40 to give 70, then add 6 and 6 to get 12 then add 12 to 70 to get 82.
Students who have successfully understood the part/whole methods in the Smart Doubling unit will have little trouble learning the Make a Ten part/whole strategy. Teachers should expect those students who failed to make the part/whole connections with doubles to also struggle with this unit. It may be best not to introduce this unit until the students understand the doubling strategy.
Getting Started
- Check the students’ knowledge of the addition facts that add to ten facts before starting. This unit builds on the students’ knowledge of the known facts of ten, i.e., 1 + 9 = 10, 2 + 8 = 10, 3 + 7 = 10, 4 + 6 = 10, 5 + 5 etc.
- Also check that the students understand the " teen" numbers. For example, show the students a ten and a four on tens frame as shown. They should respond that 10 + 4 is 14 without needing to count-on by ones
 |
- Pose an addition problem where one of the numbers is just under 10:
Anaru has 9 pink lollies and 6 yellow lollies. How many lollies does he have altogether?
Ask the students to model this with counters on tens frames.
 |
- Ask the students to think about ways that they could make this problem quick (or easy) to solve. Encourage the students to think of ways that do not involve counting on by ones.
For example, Anaru moves a yellow lolly to the pink lollies. Now ten and five is shown.
 |
It is important to discuss the fact that the answer to 9 + 6 is the same as the answer to 10 + 5. Without this realisation students will not be able to make progress into mental number processes.
(Note: Although the problem can of course be correctly solved by counting-on the aim of the lesson is to encourage the development of part/whole mental strategies.)
Exploring
Over the next 3-4 days the students are encouraged to use "Make to ten" strategies for solving number story problems.
- Make up number stories for 9 + 7, 5 + 8, 9 + 8, 7 + 6. Students use counters on empty tens frames and use the technique of filling one of the frames up to show ten counters.
- Students now use the pre-printed tens frames.
Moana has 7 oranges and 9 apples. How many pieces of fruit does she have altogether?
Ask the students to show 7 + 9 with a pre-printed 9 card and a pre-printed 7 card. Students imagine moving 1 out of the 7 to leave 6, and adding 1 to the 9 to create 10. This action of imagining pushes the student towards understanding the movement of numbers around within a problem as a key to mental processing. - Only you, as the teacher, have the pre-printed tens frames. Hold the cards so that only you can see the dots and the students have to imagine what you are seeing. Prior to giving the students addition problems ask the students to first imagine single numbers.
I can see the 8 card. What does it look like?
Some students will see the 5 + 3, others will "see" the two spaces. - Next pose addition problems, which encourage the students to imagine the tens frames that only you can see. For example:
I can see 8+ 6. How could I move the dots to work that out 8 + 6? - The next step in the progression involves no materials. The students imagine the tens frames to move around dots as they solve problems:
8 + 5, 3 + 9, 8 + 9. - Link the doubles to the Make a Ten strategy.
Ask the students to consider all the ways they know to work out 8 + 9. The range of likely responses is:
- Double 8 + 1 = 16 + 1 = 17
- Double 9 – 1 = 18 – 1 = 17
- Double 10 – 1 – 2 = 20 – 1 – 2 = 19 – 2 = 17 (Rarely used)
- 10 + 8 = 18 but this is 1 too many so the answer is 17
- Remove 1 from the 8 and add 1 to the 9 and to give 7 + 10 which is 17
- Add 2 to the 8 and remove 2 from the 9 and to give 10 + 7 which is 17
Students work out and discuss the variety of strategies to work out: 6 + 8, 9 + 7, 6 + 9
- Attention now turns to using Make a Ten strategies to solve subtraction problems. Subtraction problems with the first number in the teen decade are given.
Michael has 13 lollies and he eats 5 of them. How many lollies does Michael now have now?
Students model 13 on pre-printed ten frames.
 |
Two equally good methods are likely.
EITHER remove the 3 to leave the 10 then remove a further 2 to leave 8.
OR remove 5 from the 10 to leave 5 and add the 3 to give 8.
- Students use pre-printed tens frames to solve number stories for subtraction problems. Use: 14 - 6, 17 - 8, 12 - 8, 17 - 5, 13 - 5, 13 - 7, 14 - 3.
Notice the presence of subtractions like 17 - 5. They prevent the mindset that may develop that make a ten is always appropriate. In fact, in this example, breaking the ten is not necessary because 7 - 5 = 2 and add the 10 back in gives 12.
- Takeaways by adding.
Charlotte thinks of a way to work out 13 - 9 by adding. She asks "9 and what makes 13?" and comes up with the answer 4.
Ask the students how they think Charlotte does this. (She has gone 9 + 1= 10, she remembers the 1, she goes 10 + 3 = 13 and adds the 1 to the 3 to get 4.)
- Uses Charlotte’s addition method to work out these:
12 – 9, 14 – 8, 17 – 14, 16 - 7 - Choosing the best way:
Use either an addition and a subtraction way to work these:
13 - 9, 13 - 4, 17 - 15, 17 - 2, 19 - 17 , 12 – 8.
Reflecting
At the end of each session encourage the students to share and discuss answers as a group or class.
Dear Family and Whanau
At school this week we have solved addtion and subtraction problems using a strategy called "Making Tens". You can help your child by asking them to explain their thinking as they solve the problems on this sheet.
Making Tens
- To work out 9 + 7 Moana removes 1 from the 7 to leave 6 and adds this 1 to the 9 to make 10. She then knows 9 + 7 = 10 + 6 so the answer is 16.
Use Moana’s method of making a ten to work out these:
 |
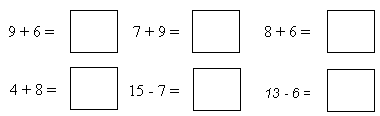- To work out 9 + 8 William knows a number ways.
- His first way is 9 + 9 = 18 and remove 1 to give 17
- His second way is to remove 1 from the 9 to leave 8 then add 8 and 8 to give 16, then put the 1 back to give 17.
- His third way is to remove 2 from the 9 to leave 7, then add 7 and 7 to give 14 then add on the 2 to give 16
Write stories to show two different ways to work out the following:
9 + 7
Story One
Story Two
15 - 9
Story One
Story Two
Similar Resources
Up we go
In this unit we work on word problems about climbing up steps and riding in a lift. We learn about different types of problems that can be modelled on number lines. We practice mental calculations with sums to 10 and to 20.
Partitions
This unit is about partitioning whole numbers. It focuses on partitioning numbers to “make a ten” or a decade when adding whole numbers, for example 8 + 6 can be solved as (8 + 2) + 4. The unit uses measurement as a context.
Ways to Add
In this unit students explore different ways to communicate and explain adding numbers within ten. The representations included are number lines, set diagrams, animal strips and tens frames.
Compatible numbers to ten
These exercises and activities are for students to use independently of the teacher to practice number properties. Some of these activities would be suitable for homework. Others require follow-up during teaching sessions.
The Number Partner
This unit uses one of the digital learning objects, the number partner, to support students as they investigate possible pairings for numbers from 10 to 30. It is suitable for students working with Advanced Counting and Early Additive strategies (Stage 4-5 of the Number Framework). It includes problems and questions that can be used by the teacher when working with a group of students on the learning object, and ideas for independent student work.
