This unit develops students’ understanding of, and proficiency in, counting one-to-one.
- Understand that the number of objects in a set stays the same as changes are made to spatial layout, size, or colour.
- Understand that the count of a collection of objects can be trusted and worked from as objects are added or taken away, or the set is rearranged into parts.
Gelman and Gallistel (1978) provided five principles that young students need to generalise when learning to count. These principles are:
- The one-to-one principle
Just like in reading when one spoken word is matched to one written word, counting involves one-to-one correspondence. One item in a collection is matched to one spoken or written word in the whole number counting sequence. - The stable order principle
The spoken and written names that are said and read have a fixed order. If that order is altered, e.g. “One, two, four, five,…”, the count will not work. - The cardinal principle
Assuming the one-to-one and stable order principles are applied then the last number in a count tells how many items are in the whole collection.
The first three principles are about how to count. The final two principles are about what can be counted.
- The abstraction principle
Items to count can be tangible, like physical objects or pictures, or they can be imaginary, like words, sounds, or ideas, e.g. Five types of animal. - The order irrelevance principle
The order in which the items are counted does not alter the cardinality of the collection. This is particularly challenging for students who think that counting is about assigning number names to the items, e.g. “This counter is number three.”
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- providing extended opportunities to practise counting and working with the equipment
- supporting students to use counting strategies to confirm any changes made to sets, if needed (sessions 4 and 5).
The contexts for activities can be adapted to suit the interests and experiences of your students. Examples may include:
- Instead of using frogs in Session 3, kiwi in burrow or native birds on branches could be used. Consider using picture books that feature these native birds to further engage your students.
Te reo Māori vocabulary such as pepeketua (frog) as well as counting in Māori could be introduced in this unit and used throughout other learning.
- Hundreds board
- Slavonic abacus
- Dominoes
- Frog animation
- Copymaster 1- Odd one out
- Copymaster 2 - Pattern cards
Students need to simultaneously develop proficiency with number sequences forward and backwards by one, and their capacity to apply those sequences to counting tasks. Ideally students’ ability to say word sequences develops either ahead of, or synchronous to, their need to apply it, so students who can count collections up to ten should be learning number sequences beyond ten.
Session 1: Hundreds board
Count by ones on a hundreds board, both forwards and backwards, and ask questions which help students connect numerals to spoken words. For example,
Can you find the number 8 without counting up or down?
What number comes after eight?
What number comes before eight?
Variations
Have students work in pairs. They take turns drawing a numeral card out of a container, then work together to find the number on a hundreds board and make a set which contains the number they have drawn, for example a set of eight counters.
First work with numbers 1–10 (tahi to tekau), and extend the range as needed to increase the challenge.
Session 2: Slavonic abacus
Count by ones on a Slavonic abacus, both forwards and backwards. While you count, say the numbers out loud with students as you move the beads. This supports them to connect the spoken word and the quantity.
Can you find the bead for number 7?
What number comes after seven?
What number comes before seven?
Note that when practising the backward number sequence it is the amount that remains, not the bead removed, that is counted. Zero is an important number to say at the end, as the expression of the absence of quantity (no beads).
Variations
Have students work in pairs. They take turns to draw a numeral card out of a container, and challenge their partner to find the number on the Slavonic abacus. If needed, they can count the beads together to check that the right bead has been identified.
First work with numbers 1–10, and extend the range as needed to increase the challenge.
Session 3: Frogs in a bucket
- Link the number after and before a given number, to adding one and subtracting one from a given collection. Use toy animals or other objects and a plastic container so there is a loud ‘plunk’ as objects go into the container. The frog animation gives an example of this with frogs in a bucket.
We had 15 frogs and one jumped out.
How many frogs are in the bucket now? - Increase the number of objects in the container beyond ten so that students attend to the one more/one less principle rather than image actions inside the container. Avoid putting in the objects one at a time after ten. Throw them in as imaginary groups. For example, a nice sequence is…
17 frogs and one more… 29 frogs and one more… 99 frogs and one more
7 frogs and one less… 15 frogs and one less… 27 frogs and one less…
Variations
If needed, link explicitly to the number sequence by referring to a hundreds board.
Extend the problems to two more/less, three more/less and beyond as students’ understanding and control of sequences grows.
Have students work in pairs, with one student putting objects into a container, and the other student listening and counting how many.
Session 4: What’s changed?
- Begin with a set of objects in a readily subitised arrangement. For example, begin with a set of six cars.
- Tell the students: Take a photograph of the collection and stash it in your mind.
Now close your eyes, and I’m going to change something.
Try to hold the picture in your mind. - Change the objects for a different kind – vary shape, colour and size to add more challenge. For example, change the cars for teddies.
- Now open your eyes. How many things can you see now?
Look for students to recognise that the number of items is unchanged though the items vary from the original ones. Aim for acceptance that the number is unchanged by means other than one-by-one counting, though use counting as a ‘fall back’ strategy if needed.
Variations
Students may begin to say the number is invariant because it has been the last few times, without necessarily accepting that number is conserved. Introduce the one more/one less principle with this activity. Vary the number of new objects by one while still retaining the original layout and see if the students detect the change and trust invariance enough to build on it.
Make the variations more significant such as adding or subtracting more than one and changing some parts of the arrangement.
Have the students work on the activity Odd one out in pairs, using Copymaster 1:
Students work with sets of three cards, and identify one difference between each card and the other two cards in the set. For example, possible answers for the cards with teddies are: the top card is different from the other two because the teddies are sitting down; the middle card is different from the other two because there are different amounts of teddies in each row, and the bottom card is different from the other two because there are 9 teddies.
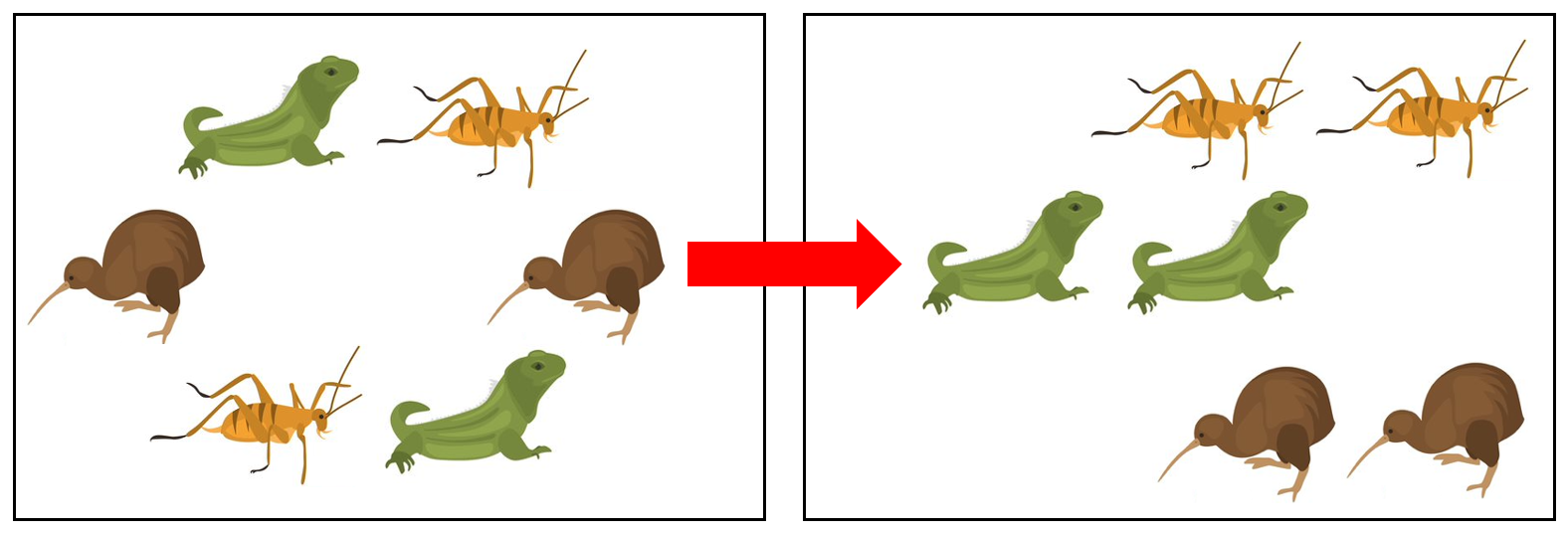
Session 5: Is there the same number?
- Lay out two collections one above the other, with items aligned.
Have a look at this collection. Are there more blue teddies, more green teddies or are there the same number? Encourage your students to equate the length of a collection with the quantity of items. - Tell the students: Take a photograph of this collection and stash it in your mind.
Now close your eyes, and I’m going to change something. - Change the spatial layout of the objects, by spreading out one of the collections.
- Now open your eyes. Are there more blue teddies, more green teddies or are there the same number?
Variations
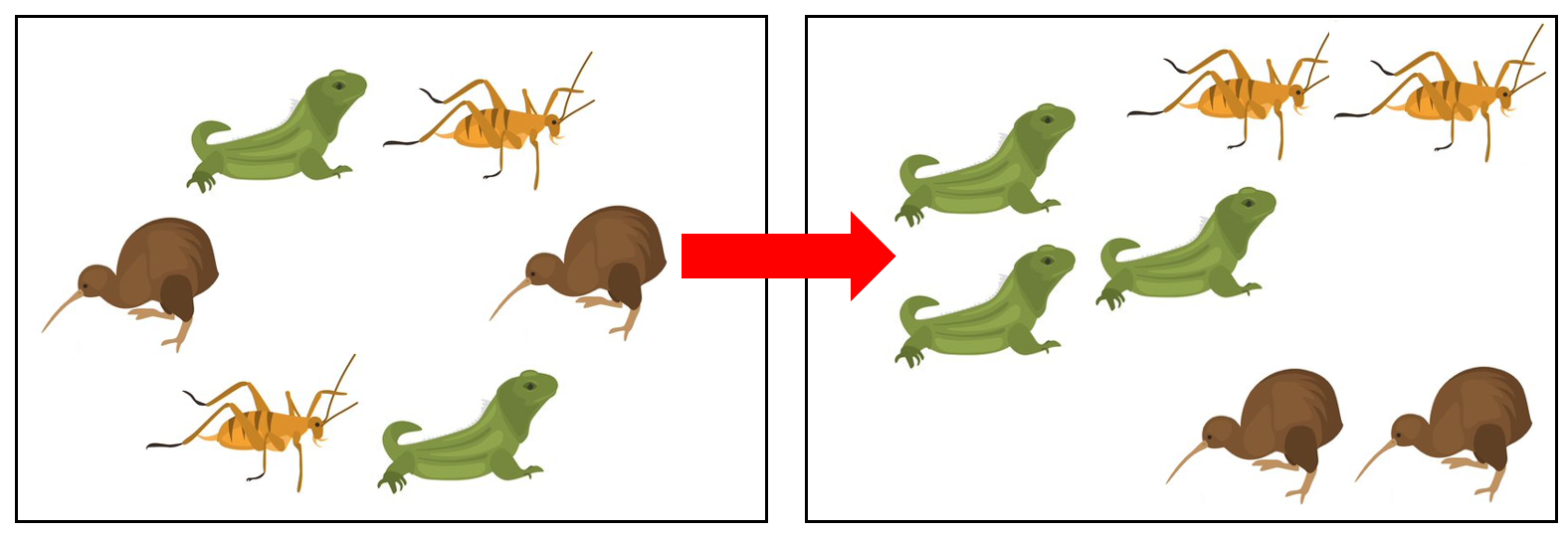
Vary the spatial arrangement of sets. Begin with a set of objects with some similar characteristics so that students can easily recall the objects that are present. For example, Take a photograph in your mind of the collection. Close your eyes and tell me what you see. Encourage students to pay attention to structure and the organisation of the set, with responses such as “There were two of each animal”, “The animals were on a hexagon”, and “Two on the top, two in the middle, two on the bottom.”
Now I’m going to change something. Vary the spatial layout of the objects, particularly expanding or contracting the length or area of the collection, or rearranging the layout.
Now open your eyes. Are there still the same number of objects? How do you know?
Make minor variations to the total number as well as the spatial layout so that students are required to trust the invariance of the count and build with it or take from it.
Have students work on the activity Domino Count in pairs. This task encourages students to trust the count in the face of different spatial arrangements.
Working with at least one set of dominoes, students sort the dominoes into groups that have the same number of dots, in total. Each group can be labelled with a numeral card, or students could make their own labels. For example:
Once the dominoes have all been grouped, students can arrange the dominoes in a pattern and write the number fact for each domino. For example,
Session 6: Counting dots
The abstraction principle involves the idea that non-tangible items such as sounds, touches, and ideas can be counted. Developing students’ capacity to count items they cannot see and feel is important because it helps them to realise that numbers are ideas.
Messages
Play the game Messages as a class:
Students sit in pairs, back to back, with one student from each pair facing the teacher. The teacher shows a pattern card from Copymaster 2 for a short time. The students turn around and gently tap the number of dots they saw on their partner’s back. The partner shows how many taps they felt by holding up that many fingers. Both players turn around to check whether the number of fingers matches the number of dots on the pattern card. Alternatively, a digit card can be held up instead of a pattern card.
Pattern memory match
Students play pattern match in groups of three or four. Each group needs a set of pattern cards (Copymaster 2) and a set of digit cards.
The pattern cards are spread out individually, face down on. The digit cards are shuffled and put in a pack, face down, in the centre. Players take turns to turn over the top digit card then turn over one of the pattern cards. If the cards match the player keeps both cards and has another turn. Once all of the cards are matched the player with the most pairs wins.
After the game, talk with students about how they recognised some patterns instantly. Look for students to use combinations of smaller groupings, e.g. “I know it’s seven because four and three are seven.”
Dear family and whānau,
This year we are learning about counting. We need to know the skills of counting like saying the numbers in the correct order forward, like "one, two, three..." and backwards, like “ten, nine, eight…”, and matching words and objects one to one.
We also need to understand that counting tells us how many objects are in a collection. We need to trust that once we have counted a collection then that number stays true even if we move the items in the collection around.
Keep looking for chances to practise counting with your child. Ask them to predict how many before they count things, like "how many forks do you think there are in the drawer?" "I've found one more fork. How many do we have now?"