These are level 3 number and statistics problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (326 KB)
find outcomes using a tree diagram (Problems 1 and 3)
use addition and subtraction facts to solve problems (Problem 4)
Problem One
This is an ideal problem for students to act out by taking the parts of Celia, Ally, and Bert. Making an organised list is another useful strategy:
CAB ACB BAC
CBA ABC BCA
The solution can also be found by using a tree diagram:
Extending the problem by adding another person to the bus stop line increases the number of possible orders to 4 x 3 x 2 x 1 = 24, which is 4! (called “four factorial”).
Problem Two
Focusing on the way in which the digital clock shows times such as “5 minutes past 8” (that is, 8:05) will be significant for some students.
Students may discuss whether 1:01 is the next time to meet the criteria. Although it is mathematically correct, in that 01 is the same as 1, this problem requires both the hour number and the minute number to look the same.
Extend the problem by suggesting that 10:01 is a “mirror” time with the colon acting as the line of symmetry. Ask students to find other mirror times, such as 12:51.
Problem Three
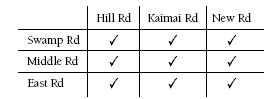
This problem is very similar to Problem One in that it involves finding all the possible combinations.
Productive strategies include making an organised list, drawing a tree diagram, and making a table. For example, a table of the problem would be:
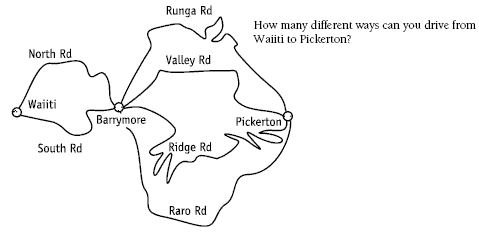
To see whether students can generalise their strategies, give them a similar problem, such as:
How many different ways can you drive from Waiiti to Pickerton?
Problem Four
As 2 and 3 have a difference of one, it is possible to show all the integers ( … -4, -3, -2, -1, 0, 1, 2, 3, 4 … ). Encourage students to use the smallest number of key presses to show them. For example:
Get students to experiment with other keys, such as 5 3 + – = , to see what numbers can be shown.
Answers to Problems
1. a. 6
b. 24
2. 10:10
3. a. 6
b. 9
4. a. 2 + 2 + 3 =
b. It is possible to get all integers.
For example, 8 is 3 + 3 + 2 =
and -1 is 2 – 3 =