Investigating the Idea of Cos

Session 1

In this session we define the cosine function and use this definition to find various values of cos(θ). Cosine is, for reasons which will become clear, like tan, what is called a circular function.

1. Begin this session with a light-hearted test (with a serious purpose). This is revision of material learned in a previous unit: Investigating the Idea of Tan. Present, in random order, each of the values that have tans that are easy to name: 0°, 30°, 60°, 120°, 180°, 45°, 135°, 225°, -45°, -135°, -120°, 90°, -90°, 270°, and so on. Get the students to write down, based on their understanding of the definition (and their memorisation of √3 and its reciprocal), the tan of each of these angles.

2. Then give them questions like this:
   If you know that an angle has a tan of √3, can you name two values that that angle might have?

3. These light-hearted tests are very important because they consolidate the ideas presented above. Mostly the answers depend on little more than a sound understanding of what tan means. The only exceptions are the surd values, but these involve simply memorising two simple facts.

4. Get each student to draw a set of axes and a unit circle (say 5cm in radius). Thus, here, 5cm is equivalent to one unit in length.

5. Now get the students to make a ruler calibrated in units and tenth of units using a strip of paper (or light cardboard) as the ruler. This ruler will be used to make measurements of cos of an angle for a unit circle of radius 5cm without the students needing to continually convert from a standard ruler. This special ruler will have 1 unit equivalent to 5cm and 0.1 of a unit equivalent to 0.5cm.  

6. Show them the definition (the idea) of cos of an angle. See Diagram 1.1.

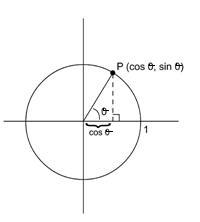
Explain that cos of an angle is the x-coordinate for the point P on the circle. The y-coordinate is called sin of the angle, but sin is not the subject of this unit of work.

7. Get the students to carefully draw an angle of 50° and to measure (with their newly made ruler) cos of 50°. They should get a value of about 0.64 units. Ensure that every student understands this definition of cos(50°). Now do the same for cos(60°) and cos(40°). Their answers should be approximately 0.5 units and 0.77 units respectively.

8. Once you are confident that the students understand what the definition of cos of angles between 0° and 90° is, move on to discuss the definition for angles between 0° and -90°. Explain that the definition is the same as above, and that clearly, in this case, the value of cos will be positive.

9. Ask the students to use the unit circle (and the paper ruler) to find cos(-35°) and cos(-80°). The answers should be about 0.82 and 0.17, respectively.

10. Now move on to explain how the definition is to be understood for angles in the second and third quadrants (angles between 90° and 180°, and angles between 180° and 270°, respectively).

11. Get the students to draw and measure cos(260°). Their answers should be approximately -0.17. Now try cos(145°). Their answers should be approximately -0.82.
    It is crucially important that every student fully understands the definition (the idea) of cos and can find cos of the sorts of angles mentioned above.

12. At this point you can check to see if they have understood what you have shown them by asking them to find the angle which has a cos of 0.7 units. Those who understand should mark the point on the unit circle which has an x-coordinate of 0.7 and draw a line between it and the origin and measure the angle. The answer is approximately 46°.

13. Now ask them if this is the only answer. Hopefully the students will realise, if they haven’t already done so, that there is another angle that also has a cos of 0.7. It is in the fourth quadrant and is approximately 314° (or -46°). The fact that there are at least two answers to these sorts of questions is a very important point and worth stressing.

14. Finish this session by getting the students to make a poster that shows what the meaning of cos is.

Sessions 2 and 3

In these sessions students are asked to fully investigate the nature of cos.

1. Begin each of these sessions with yet more light-hearted tests (with a serious purpose). Present, in random order, each of the values that have tans that are easy to name: 0°, 30°, 60°, 120°, 180°, 45°, 135°, 225°, -45°, -135°, -120°, 90°, -90°, 270°, and so on. Get the students to write down, based on their understanding of the definition (and their memorisation of √3 and its reciprocal), the tan of each of these angles. Then give them questions like this:
   If you know that an angle has a tan of √3, can you name two values that angle could have?

2. Next revise the definition of cos introduced in Session 1.

3. Investigation Instructions: Using pencil and paper find out as many interesting facts about cos as you can. You should draw a unit circle of size 5cm and use the special ruler calibrated for this circle.

4. If a student has fully understood the definition of cos they will be able to participate in this investigation. The investigation is mainly allowing the students to pinpoint and articulate the sorts of results that they will know by intuition based on the work done in Session 1. In this investigation they will systematically explore the nature of cos and write down what they find.

5. This is a broad domain of investigation and many students will be able to work out for themselves many important results. Some may need some guidance, but do not give this too readily because this will detract from the fact that this activity is an investigation of an idea. You need to trust that the work you did in Session 1 is sufficient for the students to do this investigation. However, if guidance is needed, here are some suggestions:

• Why is it easy to name the value of cos(0°)? Which other values are similarly easy to name. List them all.
• Why is the value of cos(90°) easy to name? Which other angles are similarly easy to name? List them all.
• Describe in your own words the behaviour of the value of cos as the angle moves from 0° round to 360°.
• If you know that cos of an angle is 0.4, use a scale drawing to find one value of the angle. There is another angle that has the same cos. What is it?
• Explain why it is that if you know the cos of 10° you can easily name
  cos(^–10°), cos(170°) and cos(190°).
• If cos of an angle is negative, what can you say about the angle?
• Graph the value of cos, between 0° and 360°, by carefully drawing the angles between 0° and 90° in steps of 10° and measuring the lengths of cos.
• Does cos(θ/2) = cos(θ)/2? What other questions could you ask of this sort?

7. Students should make a poster that explains what they have discovered about cos.

8. Activity: Bring into the room a tennis ball attached to a 40cm piece of string. Swing the ball around in a circle in the horizontal plane, at a slowish but regular speed, at about eye-level for the students. The students will be seeing a one-dimensional projection of this circular motion. In effect they are seeing the behaviour of cos as the angle changes at a regular rate. What they are seeing is also the behaviour of a pendulum (if they were lying beneath the pendulum and looking directly upwards). It is for this reason that cos can be used to describe the movement of a pendulum.

Session 4

Here we find some surd values of cos and learn about the inverse of cos.

1. Begin the session with another no-stakes test. Name angles such as 90°, 180°, 270°, 360°, -90°, -180°, and 450° in random order and ask them to write down the cos. Next name values such as 0, 1 and -1. In each case ask the students to name two angles with a cos equal to that value.

2. When the students studied the unit on tan they found surd expressions for tan of 30°, 60°, 120°, and so on. In a similar way surd and other simple expressions can be found for all angles that are multiples of 30° and 45°. First find expressions for cos of 30° and 60°.

3. In the diagram below we want to find cos(60°) and cos(30°). First use Pythagoras’ theorem to find BC (=√3).

   
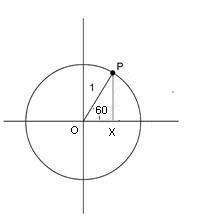
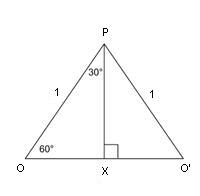
   Since OPO' is an equivalent triangle, O'P = O'O = 1. In triangle OPX, OX = 1/2. By Pythagoras' Theorem PX = √3/2. Hence cos(60°) = OX / OP = 1/2.
   What's more cos(30°) = OX / OP = √3/2.

4. Most students will wonder why it is important to know the surd expression for cos(30°). Why not just use a decimal approximation, for instance, and not one of these strange surd expressions? Point out that the square root of a prime number is irrational. And so is the half the square root of an irrational number. To put it in plain language, the value can never be written down as a decimal, no matter how many significant figures you use. And it cannot be written as a recurring decimal either. So the surd expression is exact. It also turns out that many properties of cos that the students will meet later are simpler to find if the surd (and not the decimal approximation) is used.

5. Spend some time memorising the surd expression (that is, the expression itself, not its decimal approximation): √3/2 . Spend time memorising the value of cos(30°). Spend some more time becoming familiar with the method of producing these values using an equilateral triangle and Pythagoras’theorem. Make a poster showing this method.

6. Now find a surd expression for cos(45°). A similar method can be used, but this time a different starting triangle is used (see diagram below).

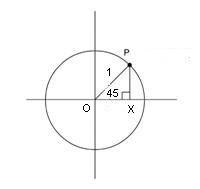
In triangle OPX, let OX = a. Then PX = a too. By Pythagoras' Theorem a² + a² = 1. So a = 1/√2. Hence cos(45°)cos = 1/√2

Use Pythagoras’ theorem again to show that AC = √2. Now scale the triangle down to half its original size. Now AB = BC = 1, and AC = 1/√2.

7. Spend some time memorising the surd expression (that is, the expression itself, not its decimal approximation): 1/√2. That is, spend time memorising the value of cos(45°). Spend some more time becoming familiar with the method of producing this value using an isosceles right angled triangle and Pythagoras’theorem. Make a poster showing this method.

8. Introduce the students to the ‘cos’ and ‘inv’ ‘cos’ buttons on the calculator. Find two values, between 0° and 360°, for θ if cos(θ) is 0.34. Do other similar examples.

9. Important: Note again that there are at least 2 angles that have a cos of 0.34, but the calculator only gives one of these. But because the students have been introduced to cos as they have been, it is easy for them to find the values that the calculator cannot give them.

Session 5

In the final session, we find unknown sides and angles of triangles.

1. Begin this session with another light-hearted test. Present, in random order, each of the values that have cosines that are easy to name: 0°, 30°, 60°, 120°, 180°, 45°, 135°, 225°, -45°, -135°, -120°, 90°, -90°, 270°, and so on. Get the students to write down, based on their understanding of the definition (and their memorisation of √3/2, 1/2 and 1/√2), the cos of each of these angles. Then give them questions like this:
   If an angle has a cos of -√3/2, what are two values that angle could have?
   These light-hearted tests are very important because they consolidate the ideas presented above.
   Mostly the answers depend on little more than a sound understanding of what cos means. The only exceptions are the surd values and the value 1/2, but these involve memorising relatively simple facts. It would be wise to continue these little light-hearted tests once the unit is completed. For instance, continue them daily for the first week following the unit and then weekly after that.

2. Now, all the above has been based on the unit circle. But what happens if we do not have a unit circle? What if the circle were of size 2, for instance? All that happens is that the previous situation has been enlarged by scale factor 2.

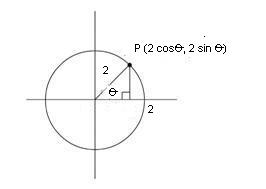
Thus the point P on the unit circle is now (2cos(θ), 2sin(θ)).

3. In general, if the circle has size r, the coordinates are (rcos(θ), rsin(θ)) (see the diagram below).

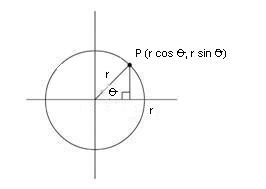
4. The unit is now finished off by applying the above to the solving of some particular right-angled triangles. This now becomes a straightforward application of the above ideas. Go through the following examples.

5. Example 1. Find the unknown, a, in the diagram below.

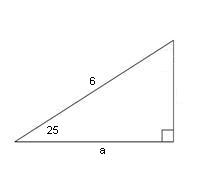
The important step is this: the student must decide which size circle to use. In this case the circle must be of size 6. Thus the problem can be shown as on the diagram below.

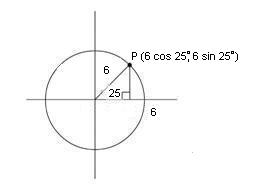
It is clear that the coordinates of P are (6cos(25°), 6sin(25°)). Clearly the unknown, a, is just the x-value of P. So a = 6cos(25°). Using a calculator we get a = 5.44 to two decimal places.

6. Example 2. Find the unknown angle, θ, in the diagram below.

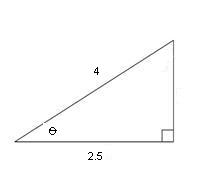
Again the important step is deciding the size of the circle to use. In this case a circle of size 4 is the appropriate one.

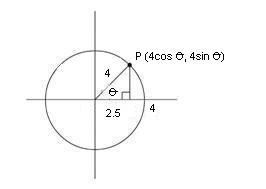
It is clear that 4cos(θ) = 2.5. All that is required is to find θ. This can be done by accurate drawing or by using the cos ^-1 button from a calculator. Obviously the latter methods is more accurate and gives 51.32 ^o to two decimal places.

7. Give the students a range of similar problems to practise on. Mix in a few examples from the tan unit so that the students learn to distinguish cos from tan cases.