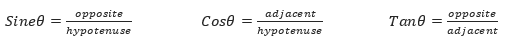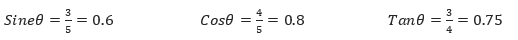In this unit students will explore the importance of triangles, particularly right angled triangles, in the real world. Students will use practical measuring skills and calculations to find a pattern linking the ratio of the sides of a triangle with the angles. Trigonometry is introduced through the use of scale diagrams.
- Measure the lengths of the sides of sets of similar right angled triangles and find the ratio of sides.
- Investigate the relationship between these ratios and the angle size.
- Use calculators or tables to find the sine, cosine and tangent of angles.
- Apply the known ratios of unit triangles (hypotenuse = 1) to find unknowns in similar triangles.
Trigonometry can be traced as far back as ancient Egypt, and possibly Babylonia. The name comes from the Greek words for triangle (trigonon – three angles) and measure (metron). Hellenist mathematicians, around 500-300 BC, applied trigonometry to the location of stars and other celestial objects.
Therefore, the origins of trigonometry lay in practical measurement tasks of finding unknown sides and angles, using right angled triangles. Medieval Persian mathematicians developed trigonometry as a separate field of mathematics, and much later, in the late 1500’s, the trigonometric (or circular) functions were developed. Many real-life situations are modelled by trigonometric functions, including the change of sea levels with a changing tide, and changing day length as a result of seasonal change.
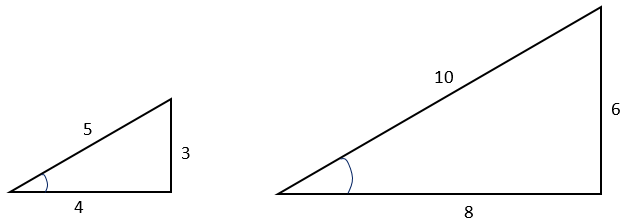
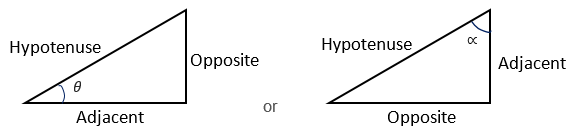
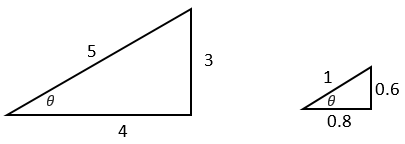
Trigonometry relies on the conservation of ratios between corresponding sides of similar right-angled triangles. Consider the case of two similar right-angled triangles. (3, 4, 5 - shown in the diagram below) and (6, 8, 10) are Pythagorean triples since 32 + 42 = 52 and 62 + 82 = 102. Therefore, the triangles are right-angled. The matching angles of both triangles are also equal (for example, the two angles marked). Less obvious is the proportional relationship between matching side lengths. The ratios 3/6, 4/8, and 5/10 are all 1/2, which gives the scale factor mapping the larger triangle onto the smaller. The reciprocal ratios (6/3, 8/4, 10/5) are 2 which is the scale factor mapping the smaller triangle onto the larger.
In fact, the matching side ratios are the same for any right-angled triangle that is similar to those two triangles. For example, the triangles (1½, 2, 2½) and (12, 16, 20) have the same side ratios. All four triangles also have the same matching angles. To formalise this idea the sides of any right-angled triangle are labelled with reference to one of the angles.
The opposite side is always ‘on the other side’ to the angle and the adjacent side is always ‘next to’ the angle. The hypotenuse is always the longest side.
The trigonometric ratios sine, cosine and tangent are the invariant side ratios for any right-angled triangle with the same angle they refer to.
For example, in the (3, 4, 5) triangle, the angle in the left diagram can be referred to as:
Let’s imagine the (3, 4, 5) triangle enlarged by a factor of 0.2 or . That means that each side of the new triangle is one-fifth the original.
The unit triangle is useful for two reasons:
- It can be scaled up or down to match any triangle that is similar. Each side length is scaled by the same factor.
- It can be used to develop the relationship between angle and sine, cosine and tangent of that angle (The trigonometric functions).
To find θ, look at the angle with a sine of 0.6, a cosine of 0.8, and a tangent of 0.75. Any one of the three ratios will do. On a scientific calculator key in:
Sin-1(0.6) = 36.87◦ (2 dp) Cos-1(0.8) = 36.87° Tan-1(0.75) = 36.87°
This unit may take longer than one week. Introducing trigonometry through scale diagrams mimics historical development which may help students to appreciate the sophistication of using trigonometric ratios to find unknown lengths and angles.
The ideas in this unit are explored further in the complementary Level 5 unit Using trigonometry.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- grouping students flexibly to encourage peer learning, scaffolding, extension, and the sharing and questioning of ideas
- apply the gradual release of responsibility to scaffold students towards working independently
- allowing the use of calculators to estimate and confirm calculations
- providing frequent opportunities for students to share their thinking and strategies, ask questions, collaborate, and clarify in a range of whole-class, small-group, peer-peer, and teacher-student settings.
The contexts presented in this unit are relevant to the real-world. However, you might choose to introduce new, more relevant, contexts later on in the unit, once students have developed the necessary understandings.
Te reo Māori kupu such as tāroa (hypotenuse), pātata (adjacent), tauaro (opposite), pākoki (trigonometry), koki hāngai (right angle), koki (angle), ōwehenga (ratio), and taurahi (scale factor) could be introduced in this unit and used throughout other mathematical learning.
Getting started
In this session the importance of right-angled triangles is discussed.
- Begin with the scenario in PowerPoint One. Ancient Egypt was one of earliest sites for trigonometry though the main story is about Thales, often regarded as the father of Greek mathematics.
Slide two introduces the problem of finding the steepness of the great pyramid. You may want to have a model of a pyramid to show how the steepness for slant height is steeper than slope along an edge. If you make a pyramid from modelling clay you can cut it vertically along a diagonal of the square base to illustrate.
You may need to discuss the measure “royal cubit” which was the length from the Pharaoh’s elbow to his longest finger (40 – 45 cm).
Ask students to use a ruler and protractor to make a scale drawing of both profiles. They should get a reasonable estimate of the angles, 51.84° for the slant height angles and 41.99° for the edge angle. These are the measures of the original pyramid which are different today due to erosion.
Discuss the exercise.
- How efficient is creating scale drawings of large buildings?
- Where can things go wrong? (Scale is a particularly important focus)
- What might the ancient Egyptians, and other cultural groups, have done to be more accurate in their plans? (Some students might suggest trigonometry)
- Show further slides of PowerPoint One to share the story of Thales’ attempt to measure the height of the great pyramid using its shadow. It is likely that Thales used a 45°, 45°, 90° triangle, meaning the shadow was the same length as the height of pole and pyramid respectively. The story is richer if he used a non-isosceles triangle as depicted in PowerPoint One.
- How might Thales use shadow length?
- What is the same about both triangles (Slide 8)?
Look for students to notice that the triangles are similar as the corresponding angles are the same. Equivalence of ratios between the side length within each triangle and between the triangles is far less obvious.
2 is two thirds of 3 and 186 is two thirds of 279.
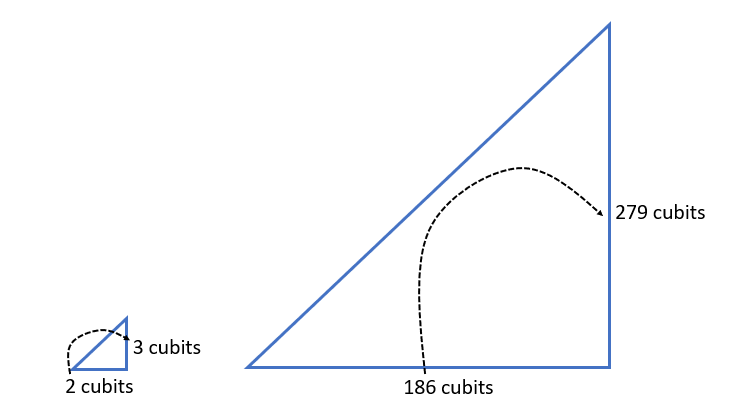
186 equals 93 x 2 and 279 equals 93 x 3. Note that 93 is the scale factor.
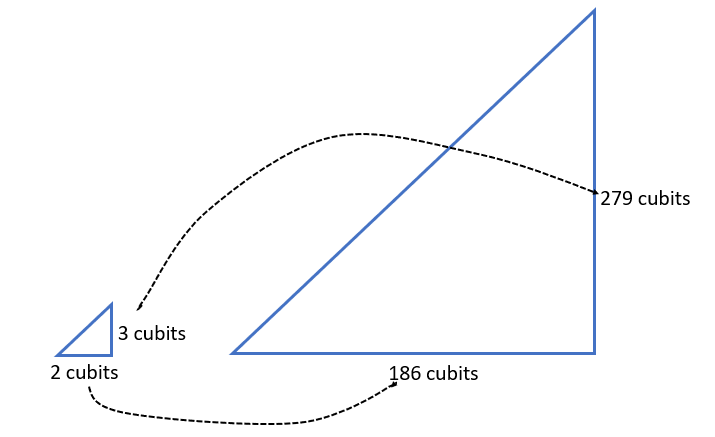
You might ask if the within and between relationships also hold for the hypotenuse. This gives an opportunity to apply the Pythagorean Theorem. The hypotenuse of the stick triangle equals √2² + 3² = 3.61 and the corresponding side of the pyramid triangle equals √186² + 279² = 335.32.
93 x 3.61 = 335.73 so the between relationship holds (allowing for rounding).
Are the within side ratios, vertical side ÷ hypotenuse, and horizontal side ÷ hypotenuse, the same for both triangles?
3 ÷ 3.61 = 0.83 and 2 ÷ 3.61 = 0.55 (stick triangle) and 279 ÷ 335.73 = 0.83 and 186 ÷ 335.73 = 0.55 (pyramid triangle). Therefore, the within side ratios are equal for both triangles. The equality of ratio within and between similar triangles is the basis of trigonometry.
- Give students Copymaster One which includes four pairs of similar right-angled triangles. Their task is as follows:
- Locate the pairs of similar triangles and check the internal angles to see they match.
- Calculate the within triangle side ratios for both triangles in each pair (opposite ÷ hypotenuse, adjacent ÷ hypotenuse, and opposite ÷ hypotenuse). To do so, students will need to nominate a reference angle. Are the ratios the same for both triangles in a pair?
- Calculate the scale factor/s that enlarge one triangle in a pair onto the other. Does the scale factor hold for each set of matching sides?
After students complete the exercise, discuss what is always the same about similar right-angled triangles. Look for students to summarise the same angles and same side ratios.
Exploring
Session Two
Last lesson we learned about Thales. Today we explore a contribution from Hipparchus, another ancient Greek, who lived over 300 years later than Thales. His great mathematical invention was the unit circle.
- Show PowerPoint Two. Hipparchus created tables of triangle values like this (see Slide One).
- What do you notice about this right-angled triangle? (Draw out the length of the hypotenuse is one)
- How might this ‘unit triangle’ be useful?
Slide Two shows an application.
- How might the height of the tree be worked out from the unit triangle?
Students may recognise that the scale factor that maps the unit triangle onto the tree triangle equals 20 ÷ 0.866 = 23.09 (2 dp). Multiplying the opposite side of the unit triangle by that scale factor gives the height of the tree, 23.09 x 0.5 = 11.55 cubits. This method may seem inefficient compared to using Tan (30°) = x/20, but the ratio tan (30°) is a pre-calculated ratio.
You may wish to carry out a practical task of creating values for the opposite and adjacent sides using a metre-long hypotenuse. Hipparchus may well have engaged in a similar task to calculate his tables, albeit with more precision.
- Provide students with a copy of Copymaster Two (enlarged to A3 if possible), chalk and a metre ruler. Ask your students to accurately draw right angled triangles with a hypotenuse of exactly a metre. Have them find the length of opposite and adjacent sides of a unit triangle for the angles, 30° (as per Slide One), 45°, 60°, and 75°. If they use millimetres as the degree of precision, they can find the values to 3 decimal places. Model the processes involved, as necessary, and roam to provide support.
- Tell students to create a table like this:
| Angle | Adjacent side (metres) | Opposite side (metres) |
| 30° | ||
| 45° | ||
| 60° | ||
| 75° |
Students might notice that the values are ‘swapped’ for 30 and 60 degrees. They might also see that the adjacent side values decrease as angle increases while the opposite side values increase.
Your calculator already has these ratios of adjacent side ÷ hypotenuse, and opposite side ÷ hypotenuse, stored as cosine and sine. Since the hypotenuse is one the ratios are the same as the values you measured, e.g. For 60°, adjacent ÷ hypotenuse = 0.5 ÷ 1 = 0.5, and opposite ÷ hypotenuse = 0.866 ÷ 1 = 0.866.
- What happens to sine as the angle increases?
- For what angle is sine equal to zero?...to one?
- How can you find cosine and sine of 54° on your calculator? Explore.
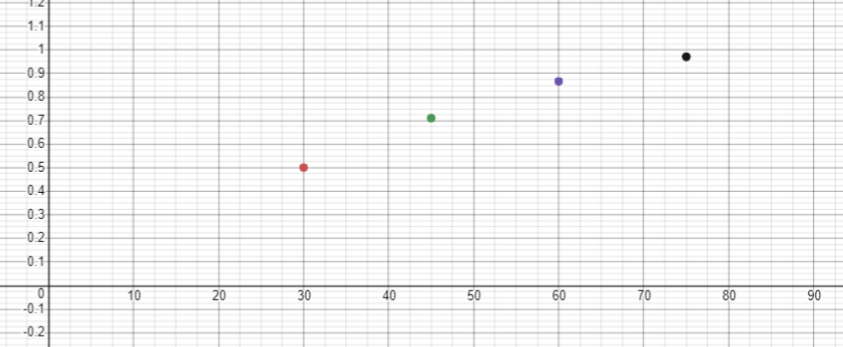
- Students should locate the cosine and sine keys on their calculator, and use them to generate cosine and sine values for given angles. Provide students with a graphing programme or a graphics calculator to generate a graph of specific values for cosine and sine in the domain 0 to 90°. Look at the shape of the collection of points, then graph the functions. The examples below are for y = sin x.
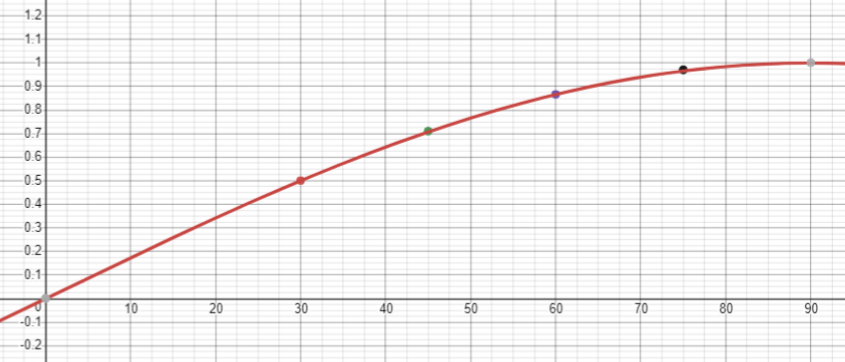
- Finish the session with the two problems on Slides Three and Four of PowerPoint Two. Slide three involves generating cosine and sine values for 65°.
- Look for students to recognise that, on Slide Four, the adjacent and opposite sides are equal since the right-angled triangle is isosceles.
The tree is 18 metres tall. The hypotenuse might be found using the Pythagorean Theorem, h = √18² + 18² , or cosine, cos(45°) = 18/h, or sine, sin(45°) = 18/h.
- Look for students to be aware that the three strategies are possible and should give the same answer.
Session Three
This session explores the nine basic problem types that can be solved using cosine, sine and tangent ratios. The important question is:
How many measurements of a right-angled triangle are needed to draw the triangle?
- Provide students with rulers, and protractors to draw the triangles. Start with the students drawing a right angle which forms one of the interior angles for the triangle. Create a die with these measurements on the faces, 37°, 45°, 63°, 6cm, 8cm, 10cm. Tell the students that you will roll the die and their job is to draw the triangle with the measures that come up. If a triangle cannot be drawn with one measure. then the die is rolled again and again until the triangle can be drawn or is it is impossible to draw.
For example, 37° might be thrown first. Students might draw this:

Some students may recognise that the angles are now set at 90°, 37°, and 63° as the sum of internal angles must equal 180°. However, without a side length the scale of the triangle is unknown.
Next 8cm is rolled. Students might draw three different figures.
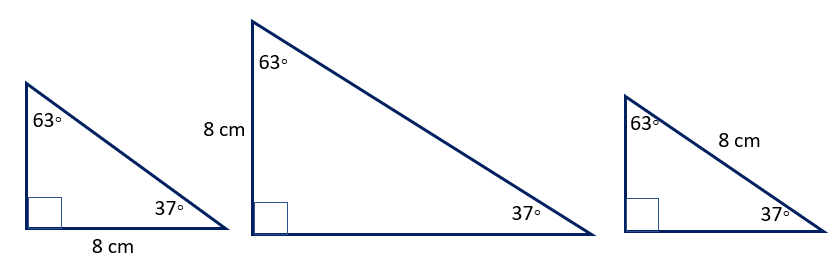
- Discuss why two measurements are not enough to create an exact triangle, but could be if the location of the side in relation to the angle of 30° was known (opposite, adjacent or hypotenuse). Discuss what might be rolled next and whether that measurement would ‘fix’ the triangle. Possibilities might be 63° (already known), 45° and 37° (impossible as sum of angles will not be 180°), 6cm (works only if 6cm is opposite the 30° angle, and 8cm is adjacent to 30°), 8cm (impossible as the triangle would need to be isosceles with angles of 90°, 45°, 45°), 10cm (works only if 8cm is adjacent to 30° and 10cm is the hypotenuse).
Try three examples of trying to draw triangles progressively from measurement information. The important generalisations to make are that it is possible to draw an exact triangle if:
- Two side lengths are known and their location relative to the right angle is known.
- One side length and one angle are known, and the location of the side relative to the angle is also known.
Knowing all three angles gives similar triangles but the size is unclear.
- Use PowerPoint Three, Slides 1-6, to discuss choosing the correct ratio, sine or cosine, to solve problems where one measure in a trigonometric ratio is missing and must be found from the information given. For each slide ask:
- What is given?
- What do we need to find?
- What ratio is needed for this problem? How do you know?
- Can you write an equation for this problem?
At this point students have not encountered tangent. Recap on what measures are given for sine and cosine to be relevant to solve a problem.
Sine is the ratio of opposite divided by hypotenuse. Cosine is the ratio of adjacent divided by hypotenuse. Show the relationships like this. After Sine and Cosine are represented by arrows ask: What ratio is missing?
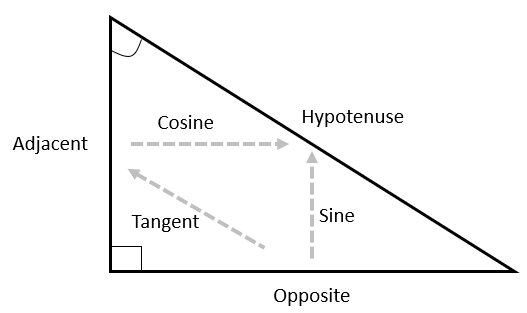
Students might notice that they do not know a ratio for the relationship between opposite and adjacent sides. Tell your students that tangent is the name for the ratio of opposite divided by adjacent. You might introduce the mnemonic SOH-CAH-TOA as a helpful way to remember the three basic trigonometric ratios. Proceed to Slides 7-9 of PowerPoint Three so student see how the tangent ratio can be applied.
Students may need more practice with identifying the ratio required for a given situation and writing the equation to be solved.
Session Four
At this point students need to solve linear equations like cos(56°) = x/16 and cos(56°) = 28/x to find unknown side lengths. Common issues students might face include:
- Regarding trigonometric ratios as a process to be carried out, rather than just a number, e.g. cos(56°) is 0.5592.
- Seeing the equals sign as a representation of transitive balance, e.g. the values of cos(56°) and x/16 are the same.
- Recognising division as one interpretation of a fraction, e.g. x/16 can mean x divided by 16.
- Understand the ‘undoing’ nature of inverse operations and how equality is preserved, e.g. Multiplying both sides by 16 changes cos(56°) = x/16 into 16cos(56°) = x.
Watch for these issues as your students work on the examples in PowerPoint Four. Pause the video where you please to allow for students to work on sub-tasks and to have discussion.
After going through the PowerPoint challenge your students to may up a similar problem for a partner to solve. Ask them to provide a full solution with all steps. Choose some examples to share with the class and put the others into a book of trigonometry problems.
For more algebra practice ask your students to work on the four learning objects in the Visual Linear Algebra suite (https://nzmaths.co.nz/content/visual-linear-algebra). Familiarity with solving linear equations is important for other aspects of the Level 5 curriculum, such as reasoning with rates and ratios, finding areas and perimeters, and conversions in measurement, and interpreting scatterplots in statistics.
Dear families and whānau,
Recently we have been using practical measuring skills and calculations to find a pattern linking the ratio of the sides of a triangle with the angles. We have used scale diagrams to learn about trigonometry. Ask your child to share their learning with you.