This unit helps students to develop procedural fluency with integers and have conceptual understanding of integers in the real world.
- Understand everyday application of integers.
- Add and subtract positive and negative integers.
- Use models to explain why subtraction of a negative integer has a positive effect.
Integers are needed to meet the demands of situations where a larger whole number is subtracted from a smaller whole number. For example, if a person has $5 available in cash but owes $8 then their net situation is 5 – 8 = -3. The origins of integers historically lie in the algebra of whole number subtraction. Integers, as quantities, usually reflect a state of balance between directional forces, such as cash being an asset and debt a liability. Furthermore, integers are sometimes called directional numbers because they represent a magnitude (size) and a direction, e.g. -3 represents a magnitude of 3 units in a negative direction from zero. The directional nature of integers is important to real world applications such as transmission factors of gears and pulleys, and to enlargement (dilation).
A common use of integers in real life is to label and quantify points on a scale, such as temperature and height above sea level. In both cases the location of zero is important to the attribute being measured. For example, both the height above normal sea level (0 m) of a spring tide and the temperature below the freezing point of water (0°C) have significant consequences to the severity of the situation. Zero acts as an important benchmark indicating normality or balance. This is also true in sport or games like Bridge where negative numbers reflect a state relative to expectation, e.g. -6 in golf means six under par when a player has taken six fewer shots than the expected norm.
Specific Teaching Points
Integers are an extension of the whole number system. Therefore, the properties of integers under the four operations should be the same as those for whole numbers. With addition and subtraction four main properties hold:
The commutative property of addition
The order of the addends does not affect the sum. If -3 + 4 = 1 then 4 + -3 = 1. Note that the commutative property does not hold for subtraction. For example, 4 - -3 = 7 but -3 – 4 = -7.
The distributive property of addition
This property is really about the partitioning of addends and recombining those addends. For example, if 5 = -1 + 6, then -2 + 5 = (-2 + -1) + 6. This property does not hold for subtraction.
The associative property of addition
This property is about ‘associating’ pairs of addends one pair at a time. For example, (-4 + 3) + -1 = -4 + (3+ -1). This property does not hold for subtraction.
Inverse operations
Addition and subtraction are inverse operations so one operation undoes the other. For example, -2 + -3 = -5 so -5 - -3 = -2.
It is the need for these number laws to hold that establishes the effect of operations, such as subtracting a negative integer has the same effect as adding a positive integer.
This unit combines two of Hans Freudenthal’s (1983) models for operations on integers, the annihilation and vector models. In the annihilation model, positives and negatives cancel each other, so +1 and -1 pairs equal zero. The act of creating or removing one positive and one negative pair that equals zero does not alter the quantity being represented. The vector model presents integers as magnitudes with direction. +1 is represented by a vector of length one in a positive direction and -1 as a vector of length one in a negative direction. Freudenthal cautioned that a quantity of +1 or -1 was easily confused with the operation of adding or subtracting one and teaching needed to make that difference explicit.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- physically moving materials and people up and down a number line to act out addition and subtraction as operations. When acting this out, addition involves facing right and subtraction involves facing left. The sign of the integer tells whether to walk forwards (positive) or backwards (negative)
- using the physical and diagrammatic models in conjunction with symbols so students can work out the answers to calculation by linking the symbols to quantities, e.g. cash as positives and debts as negatives
- modelling correct equations for calculations. Be clear about the difference between an operation symbol, and a direction symbol such as -4 which gives a direction of movement and the size of that movement
- using calculators in a predictive way - that is thinking about the answer using models, then testing out the answer on a calculator. Further to this, have students use calculators to generate patterns of equations quickly, and expect students to generalise from the patterns. For example, subtracting a negative has the same effect as adding the matching positive
- encouraging sharing and discussion of students' thinking
- using collaborative grouping so students can support each other and experience both tuakana and teina roles
- encouraging mahi tahi (collaboration) among students.
The unit uses the contexts of money, positive and negative spaces, and scale. Other contexts might better suit the interests and cultural backgrounds of your students. Students interested in sports might enjoy golf as a context, and those who enjoy computers might find points schemes interesting. Some students may enjoy the context of comparing temperatures from locations around the world, and finding out which locations have the most and least variation in a full year. Investigating local places that are above and below sea level could also be an engaging context for students.
Te reo Māori vocabulary terms such as tau tōpū (integer), tau tōraro (negative number), and tau tōrunga (positive number) could be introduced in this unit and used throughout other mathematical learning.
Session One
This session introduces negative integers in real life and presents integers as vectors.
- Begin with PowerPoint 1 that shows some situations where negative numbers are used. The contexts include temperature above and below zero degrees, water level above and below sea level, time before and after the birth of Christ, and financial well-being as a balance of available money and debt.
- For the next activity you will need sets of cards made from Copymaster 1. The cards will be used throughout the unit so investing time in laminating sets is worthwhile. Go outside and draw a horizontal number line on the pavement like this.
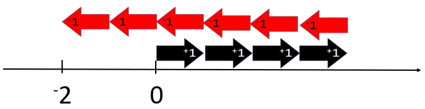
- Ask students how the number line might be extended. The real-life contexts should encourage them to consider the placement of zero and the negative integers. In the end you want a number line from -8 to 8. Mention that usually we do not write +8 for 8 though we could.
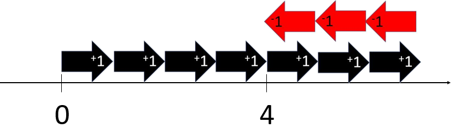
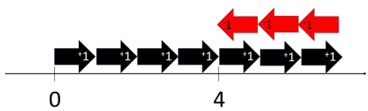
Ask one student to act out the addition of integers as vectors. Addition is the operation of combining quantities. Ask him or her to begin on zero and act out the cards they are given. Draw a set of three cards randomly (made from Copymaster 1). The +1 card represents one unit in a positive (right) direction and -1 represents one unit in a negative (left) direction. As the student walks out the movement given by the cards explain to the whole class why they are moving in that direction and the distance of that move.
Act out several combinations of cards then ask the students if it is possible to predict the finishing location if the cards are known. Choose a set of five cards and invite predictions.
What do you notice about what happens when +1 and -1 cards combine?
Is that also true of -1 and +1?
How can the fact that positive and negative cards form zeros be used to predict the finishing location? - Return inside for students to play a game of “Which way Wally Weta?” in pairs or threes. Photocopy the gameboard (Copymaster 2). Teams will need counters, preferably transparent, and a set of cards with equal numbers of +1 and -1. Each turn the cards are shuffled and the top four cards turned over one at a time. With a counter the player acts out the moves, starting at zero. They finish each play by leaving the counter at the finishing number on the board. Play continues like that for 16 turns.
The ‘house’ gets any counters on -2 or +2 and the team gets any counters that are left.
Is the game fair? - Invite students to discuss whether the game is fair, that is their team and the house have an equal chance of winning. You might look at the results of some games to see what seems to happen.
- Work ‘outside in’ to work out the ways of the counter finishing on a particular number.
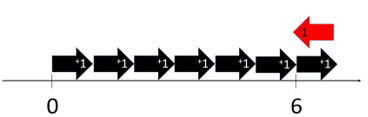
What cards will give +4? What about -4? (You might record -1 + -1 +-1 + -1 = -4 or 4 x -1 = -4.)
What cards will give you +3 or -3? (Impossible? Why?)
What cards will give you +2? (+1, +1, +1, -1) How many different orders can the cards come in?
How can you use the number of ways to get +2 to find the ways to get -2?
What other finishing numbers are possible? (Only zero – Why?)
How many orders of cards will give zero? - The game is fair as zero can be arrived at in six different card orders, meaning that the house has eight out of sixteen outcomes for them and the player has the other eight outcomes.
- A nice way to show the possibilities is to consider the ‘ordinal positions’ of the → cards only. The ← cards must take up the in between positions. Order of the cards being collected is important in determining the different ways a counter can finish at a particular place. You may need to drop back to a simpler form of the game, e.g. two or three cards to support the students with ways to find all the outcomes.
This table shows all the possible outcomes for the four card game:
Card One | Card Two | Card Three | Card Four | Total |
→ | → | → | → | 4 |
→ | → | → | ← | 2 |
→ | → | ← | → | 2 |
→ | ← | → | → | 2 |
← | → | → | → | 2 |
→ | → | ← | ← | 0 |
→ | ← | → | ← | 0 |
← | → | → | ← | 0 |
→ | ← | ← | → | 0 |
← | → | ← | → | 0 |
← | ← | → | → | 0 |
→ | ← | ← | ← | -2 |
← | → | ← | ← | -2 |
← | ← | → | ← | -2 |
← | ← | ← | → | -2 |
← | ← | ← | ← | -4 |
Session Two
In this session students explore the ‘Hills and Dales’ context for application integers. The context was used in the Oscar nominated film “Stand and Deliver” about Jaime Escalante, an American teacher working with disadvantaged students in Los Angeles. A short video of him teaching algebra using the ‘Hills and Dales’ model is easily accessed online. The video finishes with Escalante asking his students why a negative number multiplied by a negative number gives a positive answer. Good question!
In this unit the context is about road builders. In real life one of the largest costs of new roads is relocation of earth, particularly if earth must be brought in from off-site. Roads are best flat and both hills and dales present potential costs unless a hill can be used to fill a dale.
- Work through PowerPoint 2a shows some scenarios in which a hill (+1) might fill a dale (-1) to create flat land (0). With each slide ask the students two questions:
What will happen in this situation?
What is the equation for this situation?
For example, scenario one is three hills (+3) and two dales (-2). You might connect that scenario to the arrow cards by getting three +1 cards and two -1 cards. Students should recognise that you are combining integers and offer the equation 3 + -2 = 1 or -2 + 3 = 1. In fact, noting that the commutative property holds with integers is important. Work through the four scenarios before giving the students Copymaster 3 to complete independently. - For early finishers pose this problem:
The foreman notices that there are three more dales than hills.
Draw some landscapes where that would be true.
What is the same about all the landscapes you could draw? - Process the students’ answers to Copymaster 3 with emphasis on how one positive and one negative cancel out each other to form a zero. Ask what other situations in real life are like that. Situations might include having money but owing money, scoring below par and above par in golf, getting points and penalties in video games, putting hot air in the balloon and adding weights, going up in an elevator and going down, eating a hamburger and exercising hard.
- To further practise addition of integers, ask the students to play games of Integer Coverup.
- More practice with the Hills and Dales model is available in the Using integer tiles activity.
Session Three
In this session students explore the addition of Integers in the context of dollars and debts. The net financial position of a person is the sum of the money they have available and the debts they owe.
- Pose this scenario to the students:
Layla has $7 in her bank account. She owes her parents $3. How well off is Layla? - Students should tell you that Layla is worth $4 which would be the result of paying her parents off and being debt free. Her net position can be shown in many ways:
- Using toy money and IOUs
- Use vectors on a number line with +1 representing $1 and -1 representing a bill for $1.
- Using toy money and IOUs
- Whatever model is used the key point is annihilation of a one dollar debt by a one dollar coin and vice versa. Pose similar problems staying with the Layla scenario and changing the amounts. Be sure to include dollars and debts that result in a negative net position, e.g. $10 money and $13 in debts.
- Ask the students to practice this idea using the Disappearing dollars Figure It Out activity.
- Extend the dollars and debts model to subtraction of integers. Begin with Layla’s scenario with a subtle change.
Layla has $7 in her bank account. She owes her parents $3. Her parents say they will not need her to repay $2 of the debt. How well off is she now?
This story can be represented by the equation 4 - -2 = 6. Originally Layla’s position was $4, accounting for her money and debt. Removal of a two dollar debt is represented by - -2. - Ask: Is Layla better or worse off by her parents’ decision?
- Model the scenario using vectors as below.
- Initial situation
- After the removal of $2 of debt.
- Initial situation
- Pose similar problems to get a balance of starting position (positive or negative) and subtraction of both debts and dollars (spending). Adapt the Layla scenario. For example:
Layla has $8 in her bank account. She owes her parents $13. Her parents say they will not need her to repay $5 of the debt. How well off is she now? (-5 – -5 = 0)- Initial state -5
- Final state 0
- Initial state -5
- To practise subtraction using the money model students can work individually or in pairs through the e-ako called "AS4.60 More Integers (Positive and negative numbers)".
Session Four
In this session the vector model is connected to the Hills and Dales and Dollars and Debts models. The aim is to generalise addition and subtraction of integers. It is important to distinguish the vectors that represent positive and negative numbers and the addition and subtraction as operations, addition as movement to the right and subtraction as movement to the left.
- Begin with slide one of PowerPoint 4a. Ask: What do these models have in common?
Invite students to give the balance of -2. Ask: Where is -2 is in each model?
If we start with a balance of -2 and subtract 3, what does that look like in each model? - Slides 2-4 of PowerPoint 4a are animated to show what subtracting one looks like on each model. Record the operation as: -2 – 3 = -5
- Ask the students to anticipate the results on the three models of removing different amounts, particularly 2, 1 and 0. Arrange the equations in order.
-2 – 3 = -5
-2 – 2 = -4
-2 – 1 = -3
-2 – 0 = --2
What happens if -1 is subtracted (removed)? - Slides 5-7 of PowerPoint 4a model the operation that leaves the balance at -1. Continue the pattern to -2 – -3 = -1. Discuss the positive effect of removing a negative amount, that is the balance is greater than before (There is more earth and more money).
- Provide the students with a set of similar equations but starting with a positive balance, such as:
+3 – 2 = -_
+3 – 1 = -_
+3 – 0 = -_
+3 – -1 = _
+3 – -2 = _
Have them collaborate with a partner (mahi tahi) and ask them to justify their answers using one of the models that have been used.
Session Five
In this session the vector model is developed into a number line model which highlights the direction of change when integers are added and subtracted.
- Start with these True/False statements. Ask the students to have a korero about both statements in small groups.
When two numbers are added the sum is always greater than the number you start with. True or False or Sometimes True
When a number is subtracted from another the difference (answer) is always less than the starting number. True or False or Sometimes True - After a suitable period of discussion, share ideas. Look for students to state the conditions under which the statements are true or false. The first statement is true when the second addend is greater than zero (a + b > a iff b>0) and is false if the second addend is equal or less than zero (a + b ≤ a iff b≤0). Find similar conditions for the second statement, i.e. a - b < a iff b>0 and a - b ≥ a iff b≤0. Note that iff means "if and only if"
- Ask the students to work in pairs through the e-ako called "AS4.50: Integers (Positive and negative numbers)". They will learn about the direction of change through the context of Claw the Crab.
- Summarise the addition and subtraction of integers using this diagram.
- To practise the direction of change play the game Walk the Plank with students. You may like to amend the game so the dice are labelled + (for the direction of the shark, S) and – (for the direction of the boat, B). The activity could be used as a probability task where the fairness of the game is examined both experimentally and theoretically. The usual length of a game in number of rolls, before the pirate is safe or wet could also be investigated.
Dear parents and whānau,
This week we have been exploring everyday applications of integers, including using models to show what happens when adding and subtracting positive and negative integers. We have also used models to explain why subtraction of a negative integer has a positive effect.
Ask your student to show you the Hills and Dales and Dollars and Debts models to explain adding and subtracting positive and negative integers.