How much room?
In this unit we explore the amount of room we have in our classrooms. We use this to decide if the "ideal" classroom size.
construct a square metre and use it to measure areas
estimate and measure to the nearest square metre
When students can measure areas effectively using non-standard units, they are ready to move to the use of standard units. The motivation for moving to this stage, often follows from experiences where the students have used different non-standard units for the same area and have realised that consistency in the units used would allow for the easier and more accurate communication of area measures.
Students’ measurement experiences must enable them to:
- develop an understanding of the size of a square metre and a square centimetre;
- estimate and measure using square metres and square centimetres.
The usual sequence used in primary school is to introduce the square centimetre and then the square metre.
The square centimetre is introduced first, because it is small enough to measure common objects. The size of the square centimetre can be established by constructing it, for example by cutting 1-centimetre pieces of paper. Most primary classrooms also have a supply of 1-cm cubes that can be used to measure the area of objects. An appreciation of the size of the unit can be built up through lots of experience in measuring everyday objects. The students should be encouraged to develop their own reference for a centimetre, for example, a fingernail or a small button.
As the students become familiar with the size of the square centimetre they should be given many opportunities to estimate before using precise measurement. They can also be given the task of using centimetre-squared paper to create different shapes of the same area.
A square metre can be established using a similar sequence of experiences in constructing the unit and then using it to measure appropriate objects. An important learning point is that one square metre of area can take many shapes whereas a one-metre square must be a square with an area of one square metre.
Getting Started
Today we look at a metre square and use it to estimate and then measure the area of our classroom.
- Draw a metre square on the floor using chalk.
How many students do you think would be able to sit in this space?
How many of these would we need to fit all the students in our class? - Tell the students that the area is a metre square. Ask the students to estimate the area of the classroom in metre squares. Write estimates on the board.
Why do you think that many?
How did you work it out? - Ask the students to plan in small groups how they could work out the number of metre squares in the classroom. Tell the students that they need to record their ideas to share with the rest of the class.
- Share ideas for working out the area. Ideas could include:
- Covering the floor area with metres squares drawn in chalk.
- Drawing metre squares across the width of the room and the length and then multiplying the number. - As a class calculate the area of the classroom in metre squares using one of the approaches suggested. At this stage measure using whole metres only.
- Discuss how to make the measurement of the room more accurate.
What do we do about the bits left over that we haven’t included in our measurement? (join together to make metre squares or measure using metres and centimetres, for example 6 metres and 45 centimetres)
How do we find out the area when the length and width uses metres and centimetres and we want to know the area in square metres? - In order to calculate the area the measurements must be expressed in a common unit. This means that the students need to be able to express metres and centimetres as metres.
For example, 6 metres and 45 centimetres = 6.45 metres - Recalculate the area of the room using metres and centimetre measurements.
Exploring
Over the next 2-3 days we measure the area of other rooms in the school using square metres. We also record how many students are in each classroom. We use this information to draw a plan of the school.
- Tell the class that the principal wants to know if the classrooms are the right size for the numbers of students in them. To make this activity more real you could get the principal to write a letter to the class or come and ask them to undertake this activity.
- With the class list the rooms in the school that need to be measured. You may extend this to the library, hall, playing areas etc.
- Discuss ways of calculating areas when the rooms are not rectangular.
- Allocate the rooms to be measured to small groups of students. If your school has a small number of rooms then groups can measure the same room and compare measurements. Tell them to draw a plan of the room and record the measurements they make. Remind them to ask how many students are in the room.
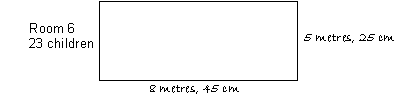
- Record the information on a class chart or on spreadsheet.
|
Room |
Length |
Width |
Area |
Number of students |
|
6 |
44.3 square metres |
23 |
||
- Discuss the class chart:
Which classroom has the largest area?
Which room has the smallest area?
Do you think that the classes are in the right rooms? Why? Why not?
Reflecting
Over 1-2 days we use the information gathered to draw a scale map of the school with areas recorded.
- Discuss how to use the information gathered to draw a scale map of the school with areas recorded. Depending on the students’ prior experience with scale maps you could look at some building plans and the scales used. For the school map a scale of 1 cm = 1 metre is reasonable.
- Get each of the small groups of students to draw a scale drawing of the classroom they measured.
- Compile a scale map of the school.
- As a class write statements to accompany the map.
- Share the map and statements with the principal as either an oral or written presentation.
This week at school we have been measuring the area of our classrooms using square metres. We have found out that we need to convert metres and centimetres to metres to do this. For example, 4 metres and 25 centimetres is 4.25 metres.
At home this week your child is to measure the area of their bedroom using square metres. They are to record the measurements on a scale drawing of their room using the scale 1 cm = 1 metre.
Similar Resources
How Can You Measure This?
In this unit students, working in groups of 2 to 4, carry out and report on a series of investigations involving decisions about how to measure something. The four investigations suggested are:
What’s In a Newspaper?
Students calculate what fraction of a newspaper is devoted to news, sport, advertisements and other categories of information.
Are You a Square?
Students determine whether their height is equal to, greater or less than, the distance from end to end of their outstretched arms.
How Far Do You Walk?
Students work out approximately how far they walk in one year.
How Thick Is It?
Students decide how to measure a length that cannot be measured directly – for example the thickness of a wall of their classroom.
In each investigation the students follow the same sequence:
- Make sure they understand the problem
- Discuss and decide on three different strategies for tackling the problem
- Complete a table to assess the merits of each strategy
- Use the best strategy for conducting the investigation
- Record their methods and results
Making Benchmarks - Length
In this unit we will explore the idea of having Benchmarks of 1 metre, 1/2 metre, and 1 centimetre to aid in estimating the length of given objects.
Visit ESOL Online for a version of this unit designed to support students for whom English is an additional language.
Measurement Investigations 2
The students will complete a number of practical measuring investigations, with an emphasis on accuracy of measuring and communication of their findings.
Round the Track
This unit is about making calculations in the real life situations of athletics.
Stepping Out
In this unit students find out the length of their pace when walking and running, and compare these with the paces of others
