The purpose of this activity is to engage students in using deductive steps, including the applications of Pythagoras' theorem to solve a problem.
This activity assumes the students have experience in the following areas:
- Finding square numbers and the square roots of numbers.
- Using Pythagoras’ theorem to find side lengths of right-angled triangles.
- Identifying common ration within and between similar triangles.
- Applying trigonometric ratios (Sin, Cos, tan) to right-angled triangles.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
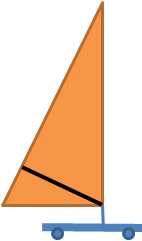
Task: A land based windsurfer is being constructed by affixing a mast and sail to a skateboard. The sail has a bar fixed to the side of the mast and going across the sail as shown in black in the diagram.
The sail is a right angled triangle with a base of 1m and the length of the hypotenuse is 2m. The bar starts at the vertex of the sail as shown and meets the hypotenuse at right angles.
Find the length of the bar.
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- What are the important conditions of the problem? (Right-angled triangle, side lengths of 2, 1 and unknown, bar at right angles to the hypotenuse.)
- What am I trying to find?
- Can I draw or sketch the situation?
- What part of the problem could I get started with? (Finding missing side lengths and angles of the sail is a good place to start.)
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- What are the maths skills I need to work this out? (Students should identify trigonometry, measurement, and algebra as potentially useful.)
- What might the solution be? What is a sensible estimate? (Why is the bar more than 1 m long?)
- What could the solution definitely not be?
- What else do I need to know to get started?
- How could I show this problem using a diagram or algebra?
- What tools (digital or physical) could help my investigation? (A scientific calculator with trigonometric functions is essential.)
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Have I shown my workings in a step-by-step way?
- Does my answer seem correct? Is it close to my estimation?
- Is there a way to verify my answer so I can convince someone else I am correct?
- How do my results look different to others? Why could this be?
- Is there another possible answer or way to solve it, that would work with any sail size?
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- What is the solution?
- Show and explain how you worked out your solution.
- Can others see how I worked it out?
- Which ideas or tools worked well in my investigation?
- Is there some mathematics that I would like to be able to do that I can't do at the moment? (Students might identify that using trigonometric ratios is an efficient way to solve the problem.)
- How can I clearly show what I found out?
- Which representation (text, table, numbers, diagram, equations) will be easy to understand?
Examples of work
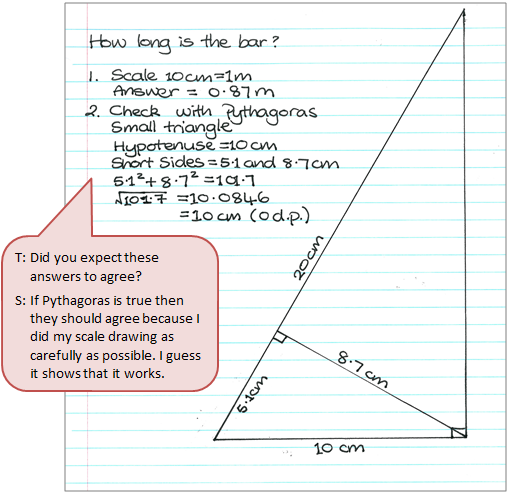
Work sample 1
The student constructs a scale diagram to solve the problem to a reasonable degree of accuracy and uses Pythagoras' theorem to verify their result.
Click on the image to enlarge it. Click again to close.
Work sample 2
The student solves a right angled triangle problem using trigonometric ratios and Pythagoras' theorem.
Click on the image to enlarge it. Click again to close.
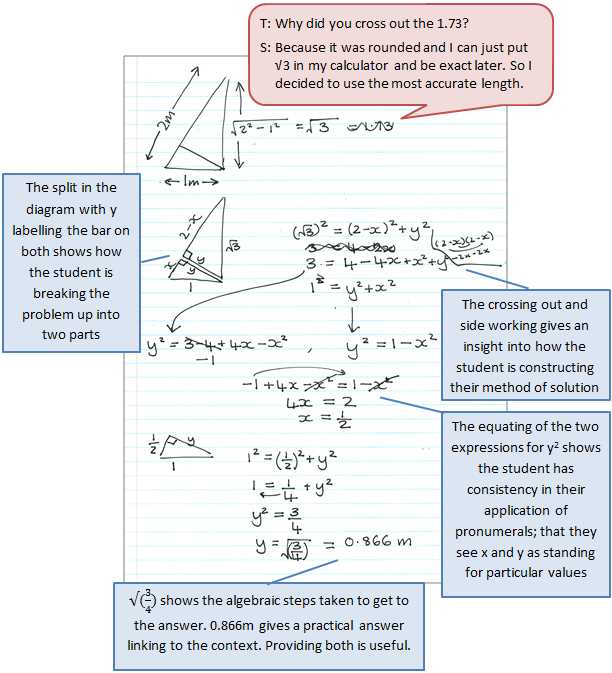
Work sample 3
The student solves a right angled triangle problem using Pythagoras' Theorem algebraicly and expresses the length with specified accuracy.