In this collection of activities we use ruler and compass constructions to draw a variety of shapes and to construct angles such as 90°, 60°, 45° and 15°.
- Apply Pythagoras' theorem.
- Use their knowledge of the sum of interior angles of a polygon.
- Construct angles based on halving and combining 90° and other straightforward angles.
- Apply knowledge of length and area.
Angle can be seen as and thought of in at least three ways. These are as:
- the spread between two rays
- the corner of a 2-dimensional figure
- an amount of turning
The final one of these underpins the others and leads on naturally to the definition of degree and the ability to measure angles with a standard unit. This then enables students to be able to apply their knowledge of angle in a variety of situations.
We see angle as developing over the following progression:
Level 1: quarter and half turns as angles
Level 2: quarter and half turns in either a clockwise or anti-clockwise direction
angle as an amount of turning
Level 3: sharp (acute) angles and blunt (obtuse) angles
right angles
degrees applied to simple angles – 90°, 180°, 360°, 45°, 30°, 60°
Level 4: degrees applied to all acute angles
degrees applied to all angles
angles applied in simple practical situations
Level 5: angles applied in more complex practical situations
The concept of angle is something that we see students developing gradually over several years. As their concept matures, they will be able to apply it in a range of situations including giving instructions for directions and finding heights. In the secondary school angle is used extensively in trigonometry (sine, cosine, tangent, etc.) to measure unknown or inaccessible distances. This deals with situations where only right-angled triangles are present in 2-dimensional situations through to more complicated triangles in 3-dimensional applications.
Surprisingly these trigonometric functions are used in abstract settings too. At Level 8 and above they are used extensively in the calculus as a means to integrate certain functions.
Outside school and university, angle is something that is used regularly by surveyors and engineers both as an immediate practical tool and as a means to solve mathematics that arises from practical situations. So angle is important in many applications in the ‘real’ world as well as an ‘abstract’ tool. This all means that angles have a fundamental role to play in mathematics and its application.
Getting started
- Remind students of the various constructions that they can perform using ruler and compasses. Talk about
How would you make a circle?
How would you make a square?
How would you make a rectangle with one side of length 10 cm and one side of length 20 cm?
How could you make an angle of 45°?
How would you make an equilateral triangle?
How could you make an isosceles triangle with base length 10 cm and other two sides equal to 15 cm? - Give the students Copymaster 1 to complete in pairs.
- Check the students’ work as they go through the tasks in Copymaster 1. Identify any areas that may require extra support before moving onto the next sessions.
- Challenge the first few students to finish, to complete the tasks in more than one way.
- When most of the class has finished, get the students to show their work and describe in mathematical language why their constructions worked.
Exploring
In the rest of this unit, students will be using the kinds of constructions that they used in the tasks of Copymaster 1 in order to make other shapes. This will require them to use ruler and compass. Students will also use their knowledge of length and area to calculate various attributes of those shapes. This is to be done in two ways (i) theoretically using their knowledge of the geometry of the shapes involved; and (ii) using measuring instruments (ruler and protractor).
Activity 1: How High?
Here students will make two shapes and determine their heights using both theoretical calculations and direct measurement.
- Discuss with the class how they would construct a scale drawing of the side of the house shown below where all of the sides are 4 m long. They will need to use ruler and compass to do this.
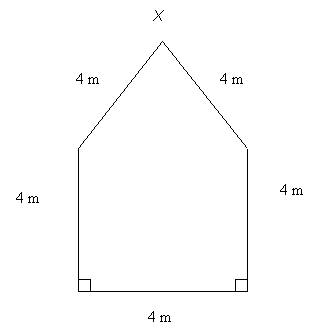
- Ask them:
How high is the highest point X above the ground?
How could you calculate this?
Can you do this in more than one way? (Theoretically and practically.) - Let the students work in their pairs on Copymaster 2.
(The height can be found theoretically by first using Pythagoras’ Theorem to calculate the height of the triangular section. This height is √(42 – 22) = √12 m. So the height of X is 4 + √12 m = 7.5 m approximately.) - Check their progress. Then let them work on the task in Copymaster 3.
(Here the other ‘base angle’ of the roof is also 45° since the triangle involved is isosceles. It is going to be helpful to calculate these angles first in order to construct the scale drawing. This means that the angle at X is 90°. In this case the height of the triangular piece is 2m – using Pythagoras or the properties of isosceles triangles - so the height of X is 6 m.) - Reinforcement problems involving Pythagoras' theorem, such as those found in textbooks and/or worksheets could be assigned or written on the board.
Activity 2
This session is very similar to the last one but this time we require the students to calculate area. To construct these drawings using ruler and compass they will need to know (i) how to find the sum of the interior angles of a pentagon; and (ii) how to construct angles of 120°, 135°, and 15°. (Now 120° is two lots of 60°; 135° is 60° plus 75° as well as 90° plus 45°; and 15° can be constructed using a 60° angle and subtracting a 45° angle.)
- Give the students Copymaster 4 and ask them to construct the shape there.
- They may need help to be able to find the required angles. If they are unable to do this in their groups you may need to hold a class discussion.
(Since the interior angles of a pentagon sum to 540°, the angle at X is 30°. The height is approximately 43.7 cm.) - The second task is on Copymaster 5.
(The height of the triangular top is approximately 0.54 m high. This can be found by direct measurement. So the area of the triangular piece is a half the base times the height = ½ x 4 x 0.54 = 1.08 m2. The square piece has area 4 x 4 = 16 m2. So the total area is 17.08 m2. Since 17.08/4 > 4, five litres of paint will be needed. This will cost 5 x 5 = 25 dollars.) - Reinforcement problems involving area, such as those found in textbooks and/or worksheets could be assigned or written on the board.
Activity 3
In this session the students are to use ruler and compasses to construct a regular hexagon (in two ways) and a regular octagon.
The regular hexagon can be completed using equilateral triangles. It can also be made by first drawing a circle and then marking off equal radius lengths around the circle. The six points so formed will make a regular hexagon.
Reflecting
In the final part of this unit the class is asked to undertake two projects that will require the use of ruler and compass.
Project 1: Design pentagonal tiles, where one of the angles is 112.5°, to tile a floor that is 3m by 5 m. Some tiles will need to be cut in order to make them fit.
(It is easiest to make tiles with right angles at the base as in the side of the house shape from earlier Copymasters.)
Project 2: Design a running track whose inside lane is 400 m long. The interior of the track should have space for a hockey field. A scale model of the track should be drawn using ruler and compass.
Allow them to find the dimensions of a hockey field by using the web. These are length 91.4 m and width 55 m. The track should be a rectangle with two semi-circles added, one at each end.
You should realise that there is no unique answer to this project. The shape of the track can be varied quite a lot without changing the fact that it allows a lane of 400 m and that it can contain a hockey pitch.
You could ask students what other playing fields the track could hold.